Правила нахождения производных. Таблицы производных
Выше, используя определение, была вычислена производная только функции  . Точно таким же образом, исходя из определения производной, можно вычислить производные и от других известных функций. Результаты сведены в следующую простую таблицу производных: . Точно таким же образом, исходя из определения производной, можно вычислить производные и от других известных функций. Результаты сведены в следующую простую таблицу производных:
1) 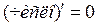 2) 2)  3) 3)  4) 4)  5) 5) 
6)  7) 7)  8) 8)  9) 9) 
10)  11) 11)  12) 12) 
Первая формула в таблице говорит о том, что если функция равна постоянному числу (или, как говорят, функция является константой), то ее производная в любой точке равна 0. В формуле  (под номером 3 в таблице производных) показатель степени (под номером 3 в таблице производных) показатель степени  может быть любым: целым положительным, целым отрицательным, дробным положительным, дробным отрицательным. Рассмотрим примеры применения этой формулы при различных типах показателя степени может быть любым: целым положительным, целым отрицательным, дробным положительным, дробным отрицательным. Рассмотрим примеры применения этой формулы при различных типах показателя степени  . Первый пример – показатель степени является целым и положительным. . Первый пример – показатель степени является целым и положительным.
Пример 1.  { { 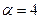 − целое положительное} − целое положительное} 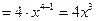 . .
В следующем примере показатель степени − целое отрицательное число. Сначала напомним определение отрицательного показателя степени: 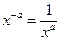 . Нам понадобится это равенство справа налево: . Нам понадобится это равенство справа налево: 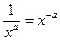 . .
Пример 2.  { { 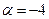 − целое отрицательное} − целое отрицательное}  . .
Дальше показатель степени − дробное положительное число. Напомним определение степени с дробным показателем:  . Нам снова понадобится это равенство в обратном порядке: . Нам снова понадобится это равенство в обратном порядке:  . .
Пример 3. 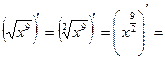 { {  − дробное положительное} = − дробное положительное} =  . .
Последний случай: показатель степени − дробное и отрицательное число.
Пример 4. 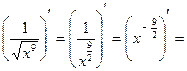 { {  − дробное отрицательное} = − дробное отрицательное} =  . .
Итак, пока мы умеем вычислять производные только от функций, перечисленных в таблице. А если формула, задающая функцию, содержит суммы, разности, произведения и частные от функций, содержащихся в этой таблице? Или содержит суперпозиции перечисленных функций (т.е. функции от функций, например, 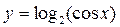 )? Для вычисления производных в этом случае используются правила, которые дает следующая )? Для вычисления производных в этом случае используются правила, которые дает следующая
Теорема.
1. Пусть функции  и и 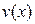 дифференцируемы в точке дифференцируемы в точке  (т.е. имеют производную в этой точке), а а − некоторое число. Тогда в этой точке дифференцируемы и функции (т.е. имеют производную в этой точке), а а − некоторое число. Тогда в этой точке дифференцируемы и функции  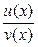 (если (если  ), а их производные вычисляются по правилам: ), а их производные вычисляются по правилам:
а) постоянный множитель  можно выносить за знак производной: можно выносить за знак производной:
(1)  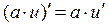
б) производная суммы-разности равна сумме-разности производных:
(2) 
в) для производной от произведения аналогия не проходит:
(3) 
г) наиболее громоздкая формула − для производной от частного (т.е. дроби):
(4) 
2. Пусть функция 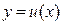 дифференцируема на некотором интервале дифференцируема на некотором интервале  , а функция , а функция  дифференцируема на области значений функции дифференцируема на области значений функции 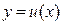 . Тогда сложная функция (или суперпозиция функций) . Тогда сложная функция (или суперпозиция функций)  дифференцируема на интервале дифференцируема на интервале  , а ее производная вычисляется по формуле: , а ее производная вычисляется по формуле: 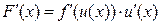 . Кратко эта формула записывается в виде: . Кратко эта формула записывается в виде:
(5) 
Для того чтобы было удобнее пользоваться формулой  для дифференцирования (т.е. взятия производной) сложной функции, эта формула сразу применена ко всем функциям, составляющим выписанную выше таблицу производных. В применении к таблице производных эта формула говорит о том, что если в таблице производных в левой части вместо для дифференцирования (т.е. взятия производной) сложной функции, эта формула сразу применена ко всем функциям, составляющим выписанную выше таблицу производных. В применении к таблице производных эта формула говорит о том, что если в таблице производных в левой части вместо  стоит любое более сложное выражение (функция стоит любое более сложное выражение (функция  ), то в правой части равенств нужно тоже поставить выражение ), то в правой части равенств нужно тоже поставить выражение  вместо вместо  , а потом еще домножить эту правую часть на производную от , а потом еще домножить эту правую часть на производную от  , т.е. , т.е.  . Результаты такого применения выписаны следующей таблице, которая называется обобщенной таблицей производных (сравните с простой таблицей производных): . Результаты такого применения выписаны следующей таблице, которая называется обобщенной таблицей производных (сравните с простой таблицей производных):
3)  4) 4)  5) 5) 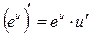
6)  7) 7)  8) 8) 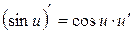
9)  10) 10)  11) 11) 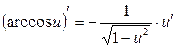 12) 12) 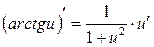
Теперь при вычислении производных от различных функций можно практически забыть о формуле для производной сложной функции, а пользоваться только простой или обобщенной таблицей производных, руководствуясь следующим правилом: если под знаком функции (синуса, косинуса, логарифма и т.д.) стоит сам аргумент  , то для вычисления производной надо использовать простую таблицу производных, а если же под знаком функции стоит более сложное выражение (представляющее собой некоторую формулу от , то для вычисления производной надо использовать простую таблицу производных, а если же под знаком функции стоит более сложное выражение (представляющее собой некоторую формулу от  ), то это выражение надо принимать за функцию ), то это выражение надо принимать за функцию  и пользоваться обобщенной таблицей производных до тех пор, пока аргументы не упростятся, после чего опять будет окончательно использоваться простая таблица. Если в обобщенной таблице производных положить и пользоваться обобщенной таблицей производных до тех пор, пока аргументы не упростятся, после чего опять будет окончательно использоваться простая таблица. Если в обобщенной таблице производных положить  , то она перейдет в простую таблицу производных. Простая и обобщенная таблицы производных, а также правила вычисления производных от суммы, разности, произведения и частного (сформулированные в теореме) позволяют вычислять производную от функции, заданной сколь угодно сложной формулой. Надо только набраться опыта в их практическом применении. А опыт появляется только после решения примеров и задач. , то она перейдет в простую таблицу производных. Простая и обобщенная таблицы производных, а также правила вычисления производных от суммы, разности, произведения и частного (сформулированные в теореме) позволяют вычислять производную от функции, заданной сколь угодно сложной формулой. Надо только набраться опыта в их практическом применении. А опыт появляется только после решения примеров и задач.
Пример 5. 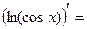  {формула 7 обобщенной таблицы производных} {формула 7 обобщенной таблицы производных}  {формула 9 простой таблицы производных}= {формула 9 простой таблицы производных}=  . .
Пример 6.  {формула 8 обобщенной таблицы производных} {формула 8 обобщенной таблицы производных}  {формула 5 обобщенной таблицы производных} {формула 5 обобщенной таблицы производных}  {формула 9 простой таблицы производных} {формула 9 простой таблицы производных}  . .
Пример 7. 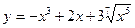 . Найти производную . Найти производную 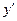 . .
Решение.  {правило (2) для производной от суммы-разности} {правило (2) для производной от суммы-разности}  {правило (1) − вынесение числового множителя за знак производной} {правило (1) − вынесение числового множителя за знак производной}  {формулы 2 и 3 простой таблицы производных} {формулы 2 и 3 простой таблицы производных}  = = 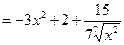 . .
Пример 8.  . Найти производную . Найти производную 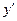 . .
Решение.   {правило (4) для производной от частного}= {правило (4) для производной от частного}=  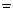 {формулы 5 и 7 простой таблицы производных}= {формулы 5 и 7 простой таблицы производных}=  . .
Пример 9.  . Найти производную . Найти производную 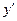 . .
Решение.  {определение дробной и отрицательной степени}= {определение дробной и отрицательной степени}=  {правило (3) для производной произведения}= {правило (3) для производной произведения}=  {формула (3) из простой и (5) из обобщенной таблицы производных}= {формула (3) из простой и (5) из обобщенной таблицы производных}= 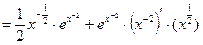   . .
Пример 10.  {определение тангенса} {определение тангенса}   {правило (4) для производной от частного} {правило (4) для производной от частного}  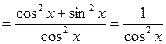 . .
Уравнение касательной
В некоторых задачах необходимо найти уравнение касательной к графику некоторой функции в некоторой его точке. Для решения таких задач требуется вспомнить данный ранее геометрический смысл производной: значение производной  в произвольной точке в произвольной точке  равно тангенсу угла наклона к оси Ох касательной к графику функции равно тангенсу угла наклона к оси Ох касательной к графику функции  в точке с в точке с
х -координатой (т.е. абсциссой), равной  . Пусть требуется написать уравнение касательной к графику функции . Пусть требуется написать уравнение касательной к графику функции  в точке графика с абсциссой в точке графика с абсциссой  (см. рисунок). Как и всякая наклонная (или горизонтальная) прямая, касательная имеет уравнение вида (см. рисунок). Как и всякая наклонная (или горизонтальная) прямая, касательная имеет уравнение вида  . Перебирая всевозможные пары чисел . Перебирая всевозможные пары чисел  и и  в этом уравнении, будем получать в этом уравнении, будем получать  уравнения всех наклонных (и горизонтальных) прямых на координатной плоскости хОу. Одна из них (при каких-то конкретных числах уравнения всех наклонных (и горизонтальных) прямых на координатной плоскости хОу. Одна из них (при каких-то конкретных числах  и и  ) даст уравнение нужной нам касательной. Найдем эти числа. Для этого вспомним, что число ) даст уравнение нужной нам касательной. Найдем эти числа. Для этого вспомним, что число  в уравнении прямой в уравнении прямой  называется угловым коэффициентом прямой и равен он тангенсу угла наклона прямой к оси Ох. Для касательной тангенс такого угла равен значению производной называется угловым коэффициентом прямой и равен он тангенсу угла наклона прямой к оси Ох. Для касательной тангенс такого угла равен значению производной  (из геометрического смысла производной). Таким образом, один из параметров в уравнении касательной найден: (из геометрического смысла производной). Таким образом, один из параметров в уравнении касательной найден: 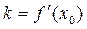 , а уравнение касательной уже можно записать в виде , а уравнение касательной уже можно записать в виде  . Оставшееся число . Оставшееся число  можно найти из того условия, что касательная должна проходить через точку можно найти из того условия, что касательная должна проходить через точку 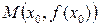 графика, т.е. координаты этой точки, при их подстановке в уравнение касательной графика, т.е. координаты этой точки, при их подстановке в уравнение касательной  , дают верное равенство: , дают верное равенство:  , откуда , откуда  . Подставляя полученное выражение для . Подставляя полученное выражение для  в уравнение касательной в уравнение касательной  , после легких преобразований получим уравнение: , после легких преобразований получим уравнение:
(1)  . .
Это и есть уравнение касательной к графику функции  в точке с абсциссой в точке с абсциссой 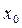 . Таким образом, для того, чтобы по формуле (1) написать уравнение касательной, нужно знать (или найти из условий задачи): . Таким образом, для того, чтобы по формуле (1) написать уравнение касательной, нужно знать (или найти из условий задачи):
1) число  − это х -координата точки графика, через которую проходит касательная к графику; − это х -координата точки графика, через которую проходит касательная к графику;
2) число  − это значение функции − это значение функции  (к графику которой строится касательная) в точке (к графику которой строится касательная) в точке  ; ;
3) число  − это значение производной от функции − это значение производной от функции  в точке в точке  . .
Пример 1. Найти уравнение касательной к графику функции  в точке с абсциссой, равной 3. в точке с абсциссой, равной 3.
Решение. Для этого примера 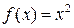 , а , а  . Тогда . Тогда   . Далее, найдем выражение для производной: . Далее, найдем выражение для производной:  . Поэтому . Поэтому  . Подставляя полученное в уравнение касательной (1), получаем . Подставляя полученное в уравнение касательной (1), получаем  или или  . Это и есть уравнение искомой касательной. . Это и есть уравнение искомой касательной.
Пример 2. Найти уравнение касательной к графику функции  в точке с заданной абсциссой в точке с заданной абсциссой  . .
Решение. В нашем примере  , ,  . Тогда . Тогда  . Итак, . Итак,  . Находим производную от . Находим производную от  : :   . Итак, . Итак,  , а потому , а потому 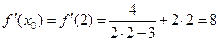 . Подставляя полученные числа . Подставляя полученные числа  и и  в уравнение касательной (1), получаем в уравнение касательной (1), получаем 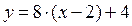 или или 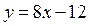 . .
Рассмотрим теперь другие типы задач на касательную.
Пример 3. Найти уравнение касательной к графику функции  в точке его пересечения с графиком функции в точке его пересечения с графиком функции  . .
Решение. В данном примере  , но неизвестна точка , но неизвестна точка 
(это, напоминаем, х -координата точки графика функции  , через которую проходит искомая касательная к нему). Таким образом, нам предстоит самим найти число , через которую проходит искомая касательная к нему). Таким образом, нам предстоит самим найти число  как х -координату точки пересечения графиков двух функций: как х -координату точки пересечения графиков двух функций:  и и  . Как известно, для этого нужно приравнять левые части уравнений, задающих эти функции, и решить получившееся уравнение: . Как известно, для этого нужно приравнять левые части уравнений, задающих эти функции, и решить получившееся уравнение:   , тогда , тогда  , а потому , а потому  . Итак, . Итак,  , а дальше можно действовать так же, как и в предыдущих примерах. Находим , а дальше можно действовать так же, как и в предыдущих примерах. Находим  . Находим производную: . Находим производную:  . Тогда . Тогда  . Подставляя полученные данные в уравнение общее уравнение для касательной (1), получаем . Подставляя полученные данные в уравнение общее уравнение для касательной (1), получаем 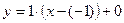 или или  − уравнение искомой касательной. − уравнение искомой касательной.
Пример 4. В какой точке параболы  касательная к ней параллельна прямой касательная к ней параллельна прямой 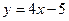 ? ?
Решение. Требуется найти некоторую точку М на параболе. Положение любой точки определяется ее координатами. Обозначим координаты искомой точки  и и  (т.е. (т.е.  ) и найдем их. Поскольку искомая точка ) и найдем их. Поскольку искомая точка  лежит на параболе лежит на параболе  , то ее вторая координата , то ее вторая координата  есть квадрат ее первой координаты: есть квадрат ее первой координаты:  . Поэтому искомая точка . Поэтому искомая точка 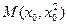 . Таким образом, для нахождения координат этой точки нам достаточно узнать только одно число . Таким образом, для нахождения координат этой точки нам достаточно узнать только одно число  − х -координату точки касания. Это число должно быть таким, чтобы касательная в соответствующей точке − х -координату точки касания. Это число должно быть таким, чтобы касательная в соответствующей точке  параболы была бы параллельна заданной прямой. Ранее (в аналитической геометрии) был приведен критерий параллельности двух прямых: прямые параллельны только в том случае, если их угловые коэффициенты совпадают. Угловой коэффициент прямой с уравнением параболы была бы параллельна заданной прямой. Ранее (в аналитической геометрии) был приведен критерий параллельности двух прямых: прямые параллельны только в том случае, если их угловые коэффициенты совпадают. Угловой коэффициент прямой с уравнением 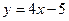 равен 4 (это коэффициент при равен 4 (это коэффициент при  в уравнении прямой, записанной в форме в уравнении прямой, записанной в форме  ). По геометрическому смыслу производной угловой коэффициент касательной к графику произвольной функции ). По геометрическому смыслу производной угловой коэффициент касательной к графику произвольной функции  в его точке с абсциссой в его точке с абсциссой  равен равен 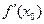 . Таким образом, для параллельности касательной и данной прямой должно выполняться условие: . Таким образом, для параллельности касательной и данной прямой должно выполняться условие:  . Это и есть уравнение, для определения . Это и есть уравнение, для определения  : найти число : найти число  , в котором значение производной функции , в котором значение производной функции  равно 4. Значение производной в любой точке равно 4. Значение производной в любой точке  для данной функции вычисляется по формуле: для данной функции вычисляется по формуле:  . Поэтому искомое . Поэтому искомое  есть корень уравнения есть корень уравнения  , т.е. , т.е.  . Учитывая, что координаты искомой точки имеют вид . Учитывая, что координаты искомой точки имеют вид 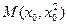 , получаем окончательно: , получаем окончательно:  . .
Производные высших порядков
Пусть функция  дифференцируема на некотором интервале дифференцируема на некотором интервале  , т.е. в каждой точке этого интервала. Тогда ее производная , т.е. в каждой точке этого интервала. Тогда ее производная  есть тоже функция, определенная на интервале есть тоже функция, определенная на интервале  . Может оказаться (чаще всего так и бывает), что она тоже дифференцируема на этом интервале. Взяв от нее производную . Может оказаться (чаще всего так и бывает), что она тоже дифференцируема на этом интервале. Взяв от нее производную  , получим функцию, которая называется второй производной от исходной функции , получим функцию, которая называется второй производной от исходной функции  и обозначается и обозначается  . Итак, вторая производная функции . Итак, вторая производная функции  определяется как производная от ее производной: определяется как производная от ее производной:   . Аналогично определяется третья производная (как производная от второй производной) . Аналогично определяется третья производная (как производная от второй производной)  и все остальные производные высших порядков. и все остальные производные высших порядков.
Пример 1. Найти последовательные производные функции  . .
Решение. Последовательно находим:  ; ;  ; ;  ; ;  . Поскольку опять получилась исходная функция . Поскольку опять получилась исходная функция 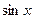 , то дальнейшие производные будут повторять те, что мы уже нашли. , то дальнейшие производные будут повторять те, что мы уже нашли.
Пример 2. Найти вторую производную функции 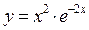 . .
Решение. Сначала найдем первую производную:
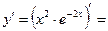   . .
Затем находим вторую производную как производную от первой производной:
 = =
={последняя производная  уже была вычислена при нахождении уже была вычислена при нахождении 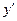 }= }=  . .
Итак, вторая производная 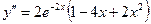 . .
Дифференциал функции
Пусть функция  дифференцируема в точке дифференцируема в точке  . Это означает, что она имеет производную в этой точке, то есть существует предел: . Это означает, что она имеет производную в этой точке, то есть существует предел:  , где, напомним, , где, напомним,  есть приращение функции есть приращение функции  в точке в точке  , соответствующее приращению аргумента , соответствующее приращению аргумента  этой функции на величину этой функции на величину  . Предположим дополнительно, что . Предположим дополнительно, что  . По теореме о бесконечно малых (см. параграф «Бесконечно малые и бесконечно большие функции», хотя интуитивно это и так понятно) соотношение . По теореме о бесконечно малых (см. параграф «Бесконечно малые и бесконечно большие функции», хотя интуитивно это и так понятно) соотношение  означает, что разность означает, что разность  стремится к 0 при стремится к 0 при  (т.е. является бесконечно малой): (т.е. является бесконечно малой):  . Обозначим эту разность . Обозначим эту разность  : :  . Выразив отсюда . Выразив отсюда  , получим: , получим:
(1) 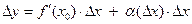 , ,
причем  − бесконечно малая при − бесконечно малая при  : :
(2)  . .
Из (1) следует, что приращение функции  состоит из двух слагаемых: состоит из двух слагаемых:  и и  . Выясним, какой относительный вклад вносит в . Выясним, какой относительный вклад вносит в  каждое из них. Составим отношение второго слагаемого к первому каждое из них. Составим отношение второго слагаемого к первому 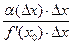 и вычислим предел его при и вычислим предел его при  : :
(3)  , ,
что следует из (2) в принятом предположении, что  . Отсюда следует, что при маленьких значениях приращения . Отсюда следует, что при маленьких значениях приращения  второе слагаемое в (1) становится пренебрежимо малым по сравнению с первым, а потому основной вклад в формирование второе слагаемое в (1) становится пренебрежимо малым по сравнению с первым, а потому основной вклад в формирование  в (1) вносит первое слагаемое в (1) вносит первое слагаемое  , которое (по этой причине) является главной частью приращения функции и носит название ее дифференциала. , которое (по этой причине) является главной частью приращения функции и носит название ее дифференциала.
Дифференциалом функции  в точке в точке  (обозначатся (обозначатся  ) называется главная часть приращения этой функции, т.е. выражение ) называется главная часть приращения этой функции, т.е. выражение  . Таким образом, по определению дифференциала . Таким образом, по определению дифференциала
(4)  . .
Поскольку, как отмечено выше, дифференциал является главной частью приращения функции (при малых значениях  ), то выполнено приближенное равенство ), то выполнено приближенное равенство
(5) 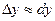 , ,
которое (в силу (1) и (3)) тем точнее, чем меньше приращение аргумента  . .
Кроме понятия дифференциала функции, вводится и понятие дифференциала независимой переменной. Дифференциалом независимой переменной  (обозначается (обозначается  ) называется ее приращение ) называется ее приращение  : :  . Поэтому дифференциал функции (4) в произвольной точке . Поэтому дифференциал функции (4) в произвольной точке  записывают также в виде записывают также в виде
(6)  . .
Основным свойством дифференциала является отмеченное в (5) приближенное равенство 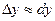 , означающее, что при малых значениях приращения , означающее, что при малых значениях приращения  независимой переменной независимой переменной  приращение функции приращение функции  приближенно равно ее дифференциалу приближенно равно ее дифференциалу  . Геометрическая иллюстрация этого приближенного равенства представлена на рисунке. На нем приращение функции . Геометрическая иллюстрация этого приближенного равенства представлена на рисунке. На нем приращение функции  , а дифференциал функции , а дифференциал функции  (это следует из рассмотрения прямоугольного треугольника (это следует из рассмотрения прямоугольного треугольника  и геометрического смысла производной: и геометрического смысла производной:  ). Таким образом, приращение ординаты (т.е. y -координаты) графика функции приближенно равно приращению ординаты касательной (прямая S на рисунке) к этому графику. Отсюда следует такой интересный факт, что из всех прямых, проведенных через данную точку графика, именно касательная примыкает к нему ближе всего. ). Таким образом, приращение ординаты (т.е. y -координаты) графика функции приближенно равно приращению ординаты касательной (прямая S на рисунке) к этому графику. Отсюда следует такой интересный факт, что из всех прямых, проведенных через данную точку графика, именно касательная примыкает к нему ближе всего.
Одним из приложений понятия дифференциала функции является его применение к приближенным вычислениям. Запишем приближенное равенство (5) более подробно, расписав в нем выражения для  и и  : :  или или
(7) 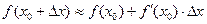 . .
Это равенство и лежит в основе применения дифференциала к приближенным вычислениям. Пусть значение некоторой функции  и ее производной легко вычисляется в некоторой точке и ее производной легко вычисляется в некоторой точке  , а нам необходимо найти значение функции в точке, близкой к , а нам необходимо найти значение функции в точке, близкой к  , но значение в ней вычислить непосредственно по формуле , но значение в ней вычислить непосредственно по формуле  затруднительно. Тогда можно использовать приведенное выше приближенное равенство (7). затруднительно. Тогда можно использовать приведенное выше приближенное равенство (7).
Пример 1. Найти приближенное значение  . .
Решение. Рассмотрим функцию  , положим , положим  , ,  . Тогда . Тогда  = =  , ,   , ,  , поэтому , поэтому  . Тогда из формулы (7) получаем: . Тогда из формулы (7) получаем:
 = =  . .
Окончательно 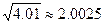 . Отметим, что точное значение . Отметим, что точное значение  . .
Пример 2. Доказать, что при малых  справедливо: справедливо:  . .
Указание. Аналогично предыдущему примеру:  , но , но  . Применить формулу (7), а затем . Применить формулу (7), а затем  заменить более приятной буквой заменить более приятной буквой  . .
|



 . Точно таким же образом, исходя из определения производной, можно вычислить производные и от других известных функций. Результаты сведены в следующую простую таблицу производных:
. Точно таким же образом, исходя из определения производной, можно вычислить производные и от других известных функций. Результаты сведены в следующую простую таблицу производных: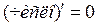 2)
2)  3)
3)  4)
4)  5)
5) 
 7)
7)  8)
8)  9)
9) 
 11)
11)  12)
12) 
 может быть любым: целым положительным, целым отрицательным, дробным положительным, дробным отрицательным. Рассмотрим примеры применения этой формулы при различных типах показателя степени
может быть любым: целым положительным, целым отрицательным, дробным положительным, дробным отрицательным. Рассмотрим примеры применения этой формулы при различных типах показателя степени  {
{ 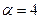 − целое положительное}
− целое положительное} 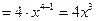 .
.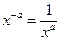 . Нам понадобится это равенство справа налево:
. Нам понадобится это равенство справа налево: 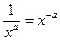 .
. {
{ 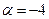 − целое отрицательное}
− целое отрицательное}  .
. . Нам снова понадобится это равенство в обратном порядке:
. Нам снова понадобится это равенство в обратном порядке:  .
.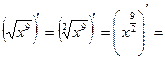 {
{  − дробное положительное} =
− дробное положительное} =  .
.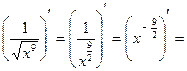 {
{  − дробное отрицательное} =
− дробное отрицательное} =  .
.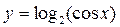 )? Для вычисления производных в этом случае используются правила, которые дает следующая
)? Для вычисления производных в этом случае используются правила, которые дает следующая и
и 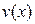 дифференцируемы в точке
дифференцируемы в точке  (т.е. имеют производную в этой точке), а а − некоторое число. Тогда в этой точке дифференцируемы и функции
(т.е. имеют производную в этой точке), а а − некоторое число. Тогда в этой точке дифференцируемы и функции 
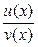 (если
(если  ), а их производные вычисляются по правилам:
), а их производные вычисляются по правилам: можно выносить за знак производной:
можно выносить за знак производной:
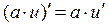



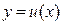 дифференцируема на некотором интервале
дифференцируема на некотором интервале  , а функция
, а функция  дифференцируема на области значений функции
дифференцируема на области значений функции  дифференцируема на интервале
дифференцируема на интервале 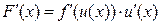 . Кратко эта формула записывается в виде:
. Кратко эта формула записывается в виде:
 стоит любое более сложное выражение (функция
стоит любое более сложное выражение (функция  ), то в правой части равенств нужно тоже поставить выражение
), то в правой части равенств нужно тоже поставить выражение  . Результаты такого применения выписаны следующей таблице, которая называется обобщенной таблицей производных (сравните с простой таблицей производных):
. Результаты такого применения выписаны следующей таблице, которая называется обобщенной таблицей производных (сравните с простой таблицей производных): 4)
4)  5)
5) 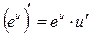
 7)
7)  8)
8) 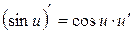
 10)
10)  11)
11) 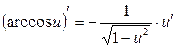 12)
12) 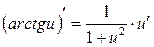
 , то она перейдет в простую таблицу производных. Простая и обобщенная таблицы производных, а также правила вычисления производных от суммы, разности, произведения и частного (сформулированные в теореме) позволяют вычислять производную от функции, заданной сколь угодно сложной формулой. Надо только набраться опыта в их практическом применении. А опыт появляется только после решения примеров и задач.
, то она перейдет в простую таблицу производных. Простая и обобщенная таблицы производных, а также правила вычисления производных от суммы, разности, произведения и частного (сформулированные в теореме) позволяют вычислять производную от функции, заданной сколь угодно сложной формулой. Надо только набраться опыта в их практическом применении. А опыт появляется только после решения примеров и задач.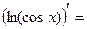
 {формула 7 обобщенной таблицы производных}
{формула 7 обобщенной таблицы производных}  {формула 9 простой таблицы производных}=
{формула 9 простой таблицы производных}=  .
. {формула 8 обобщенной таблицы производных}
{формула 8 обобщенной таблицы производных}  {формула 5 обобщенной таблицы производных}
{формула 5 обобщенной таблицы производных}  {формула 9 простой таблицы производных}
{формула 9 простой таблицы производных}  .
.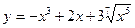 . Найти производную
. Найти производную 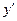 .
.  {правило (2) для производной от суммы-разности}
{правило (2) для производной от суммы-разности}  {правило (1) − вынесение числового множителя за знак производной}
{правило (1) − вынесение числового множителя за знак производной}  {формулы 2 и 3 простой таблицы производных}
{формулы 2 и 3 простой таблицы производных}  =
= 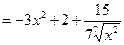 .
. . Найти производную
. Найти производную 
 {правило (4) для производной от частного}=
{правило (4) для производной от частного}= 
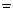 {формулы 5 и 7 простой таблицы производных}=
{формулы 5 и 7 простой таблицы производных}=  .
. {определение дробной и отрицательной степени}=
{определение дробной и отрицательной степени}=  {правило (3) для производной произведения}=
{правило (3) для производной произведения}=  {формула (3) из простой и (5) из обобщенной таблицы производных}=
{формула (3) из простой и (5) из обобщенной таблицы производных}= 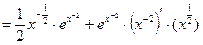

 .
. {определение тангенса}
{определение тангенса} 
 {правило (4) для производной от частного}
{правило (4) для производной от частного} 
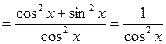 .
. в произвольной точке
в произвольной точке  равно тангенсу угла наклона к оси Ох касательной к графику функции
равно тангенсу угла наклона к оси Ох касательной к графику функции  в точке с
в точке с  . Перебирая всевозможные пары чисел
. Перебирая всевозможные пары чисел  и
и  в этом уравнении, будем получать
в этом уравнении, будем получать  уравнения всех наклонных (и горизонтальных) прямых на координатной плоскости хОу. Одна из них (при каких-то конкретных числах
уравнения всех наклонных (и горизонтальных) прямых на координатной плоскости хОу. Одна из них (при каких-то конкретных числах  называется угловым коэффициентом прямой и равен он тангенсу угла наклона прямой к оси Ох. Для касательной тангенс такого угла равен значению производной
называется угловым коэффициентом прямой и равен он тангенсу угла наклона прямой к оси Ох. Для касательной тангенс такого угла равен значению производной 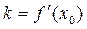 , а уравнение касательной уже можно записать в виде
, а уравнение касательной уже можно записать в виде  . Оставшееся число
. Оставшееся число 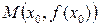 графика, т.е. координаты этой точки, при их подстановке в уравнение касательной
графика, т.е. координаты этой точки, при их подстановке в уравнение касательной  , откуда
, откуда  . Подставляя полученное выражение для
. Подставляя полученное выражение для  .
. в точке с абсциссой
в точке с абсциссой 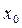 . Таким образом, для того, чтобы по формуле (1) написать уравнение касательной, нужно знать (или найти из условий задачи):
. Таким образом, для того, чтобы по формуле (1) написать уравнение касательной, нужно знать (или найти из условий задачи): − это х -координата точки графика, через которую проходит касательная к графику;
− это х -координата точки графика, через которую проходит касательная к графику; − это значение функции
− это значение функции  − это значение производной от функции
− это значение производной от функции  в точке
в точке  в точке с абсциссой, равной 3.
в точке с абсциссой, равной 3.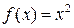 , а
, а  . Тогда
. Тогда 
 . Далее, найдем выражение для производной:
. Далее, найдем выражение для производной:  . Поэтому
. Поэтому  . Подставляя полученное в уравнение касательной (1), получаем
. Подставляя полученное в уравнение касательной (1), получаем  или
или  . Это и есть уравнение искомой касательной.
. Это и есть уравнение искомой касательной. в точке с заданной абсциссой
в точке с заданной абсциссой  .
.  . Тогда
. Тогда  . Итак,
. Итак,  . Находим производную от
. Находим производную от  :
: 
 . Итак,
. Итак,  , а потому
, а потому 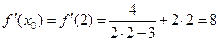 . Подставляя полученные числа
. Подставляя полученные числа  и
и  в уравнение касательной (1), получаем
в уравнение касательной (1), получаем 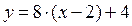 или
или 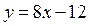 .
. в точке его пересечения с графиком функции
в точке его пересечения с графиком функции  .
. , но неизвестна точка
, но неизвестна точка 
 , тогда
, тогда  , а потому
, а потому  . Итак,
. Итак,  , а дальше можно действовать так же, как и в предыдущих примерах. Находим
, а дальше можно действовать так же, как и в предыдущих примерах. Находим  . Находим производную:
. Находим производную:  . Тогда
. Тогда  . Подставляя полученные данные в уравнение общее уравнение для касательной (1), получаем
. Подставляя полученные данные в уравнение общее уравнение для касательной (1), получаем 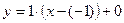 или
или  − уравнение искомой касательной.
− уравнение искомой касательной.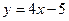 ?
? (т.е.
(т.е.  ) и найдем их. Поскольку искомая точка
) и найдем их. Поскольку искомая точка  . Поэтому искомая точка
. Поэтому искомая точка 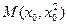 . Таким образом, для нахождения координат этой точки нам достаточно узнать только одно число
. Таким образом, для нахождения координат этой точки нам достаточно узнать только одно число  параболы была бы параллельна заданной прямой. Ранее (в аналитической геометрии) был приведен критерий параллельности двух прямых: прямые параллельны только в том случае, если их угловые коэффициенты совпадают. Угловой коэффициент прямой с уравнением
параболы была бы параллельна заданной прямой. Ранее (в аналитической геометрии) был приведен критерий параллельности двух прямых: прямые параллельны только в том случае, если их угловые коэффициенты совпадают. Угловой коэффициент прямой с уравнением  в уравнении прямой, записанной в форме
в уравнении прямой, записанной в форме  ). По геометрическому смыслу производной угловой коэффициент касательной к графику произвольной функции
). По геометрическому смыслу производной угловой коэффициент касательной к графику произвольной функции  в его точке с абсциссой
в его точке с абсциссой 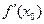 . Таким образом, для параллельности касательной и данной прямой должно выполняться условие:
. Таким образом, для параллельности касательной и данной прямой должно выполняться условие:  . Это и есть уравнение, для определения
. Это и есть уравнение, для определения  равно 4. Значение производной в любой точке
равно 4. Значение производной в любой точке  . Поэтому искомое
. Поэтому искомое  , т.е.
, т.е.  . Учитывая, что координаты искомой точки имеют вид
. Учитывая, что координаты искомой точки имеют вид  .
. есть тоже функция, определенная на интервале
есть тоже функция, определенная на интервале  , получим функцию, которая называется второй производной от исходной функции
, получим функцию, которая называется второй производной от исходной функции  и обозначается
и обозначается  . Итак, вторая производная функции
. Итак, вторая производная функции 
 . Аналогично определяется третья производная (как производная от второй производной)
. Аналогично определяется третья производная (как производная от второй производной)  и все остальные производные высших порядков.
и все остальные производные высших порядков. .
. ;
;  ;
;  ;
;  . Поскольку опять получилась исходная функция
. Поскольку опять получилась исходная функция 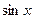 , то дальнейшие производные будут повторять те, что мы уже нашли.
, то дальнейшие производные будут повторять те, что мы уже нашли.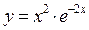 .
.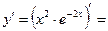

 .
. =
= уже была вычислена при нахождении
уже была вычислена при нахождении  .
.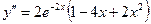 .
. , где, напомним,
, где, напомним,  есть приращение функции
есть приращение функции  . Предположим дополнительно, что
. Предположим дополнительно, что  . По теореме о бесконечно малых (см. параграф «Бесконечно малые и бесконечно большие функции», хотя интуитивно это и так понятно) соотношение
. По теореме о бесконечно малых (см. параграф «Бесконечно малые и бесконечно большие функции», хотя интуитивно это и так понятно) соотношение  стремится к 0 при
стремится к 0 при  (т.е. является бесконечно малой):
(т.е. является бесконечно малой):  . Обозначим эту разность
. Обозначим эту разность  :
:  . Выразив отсюда
. Выразив отсюда  , получим:
, получим: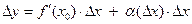 ,
, .
. и
и  . Выясним, какой относительный вклад вносит в
. Выясним, какой относительный вклад вносит в 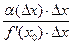 и вычислим предел его при
и вычислим предел его при  ,
, . Отсюда следует, что при маленьких значениях приращения
. Отсюда следует, что при маленьких значениях приращения  , которое (по этой причине) является главной частью приращения функции и носит название ее дифференциала.
, которое (по этой причине) является главной частью приращения функции и носит название ее дифференциала. ) называется главная часть приращения этой функции, т.е. выражение
) называется главная часть приращения этой функции, т.е. выражение  .
.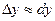 ,
, ) называется ее приращение
) называется ее приращение  . Поэтому дифференциал функции (4) в произвольной точке
. Поэтому дифференциал функции (4) в произвольной точке  .
. , а дифференциал функции
, а дифференциал функции  (это следует из рассмотрения прямоугольного треугольника
(это следует из рассмотрения прямоугольного треугольника  и геометрического смысла производной:
и геометрического смысла производной:  ). Таким образом, приращение ординаты (т.е. y -координаты) графика функции приближенно равно приращению ординаты касательной (прямая S на рисунке) к этому графику. Отсюда следует такой интересный факт, что из всех прямых, проведенных через данную точку графика, именно касательная примыкает к нему ближе всего.
). Таким образом, приращение ординаты (т.е. y -координаты) графика функции приближенно равно приращению ординаты касательной (прямая S на рисунке) к этому графику. Отсюда следует такой интересный факт, что из всех прямых, проведенных через данную точку графика, именно касательная примыкает к нему ближе всего. или
или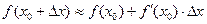 .
. .
. , положим
, положим  ,
,  . Тогда
. Тогда  ,
, 
 ,
,  , поэтому
, поэтому  . Тогда из формулы (7) получаем:
. Тогда из формулы (7) получаем: .
.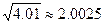 . Отметим, что точное значение
. Отметим, что точное значение  .
. .
. . Применить формулу (7), а затем
. Применить формулу (7), а затем  заменить более приятной буквой
заменить более приятной буквой 


