
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производные некоторых элементарных функции
C/=0, x/=1, (хn)/=nxn-1, (ax)/=axlna, (sinx)/=cosx, (ex)/=ex, (cosx)/= -sinx, (logax)/= Производная сложной функции. Сложная функция имеет вид: F(x)=f(g(x)), т.е. является функцией от функции. Например, y=sin2x, y=ln(x2+2x) и т.д. Если в точке х функция g(x) имеет производную g '(x), а в точке u=g(x) функция f(u) имеет производную f '(u), то производная сложной функции f(g(x)) в точке х существует и равна f '(u)g'(x) Практическая часть Пример 1. Вычислить производную функции: а) у=(5-x2+x3)(x4-3); б) Решение. а) Применим правило дифференцирования (2) ((5-x2+x3)(x4-3))/=(5-x2+x3)/(x4-3)+(5-x2+x3)(x4-3)/=(-2x+3x2)(x4-3)+(5-x2+x3)∙4x3=-2x5+6x+3x6-9x2+20x3-4x5+4x6=7x6-6x5+20x3-9x2+6x. б) Применим правило дифференцирования (3)
в) Применим правило нахождения производной сложной функции ((x4-5x3+7)5)/=5∙(x4-5x3+7)4∙(x4-5x3+7)/=5∙(x4-5x3+7)4(4x3-15x2)=(20x3-75x2)(x4-5x3+7). Пример 2. Вычислить производную функции Решение. Применим свойство (3) и правило нахождения сложной функции: Пример 3. Найти производную функции Решение.
Практические задания Найти производные функции:
Контрольные вопросы Дайте определение производной. Чему равна производная суммы, производная произведения, производная частного двух функции? Какая функция называется сложной? Чему равна производная сложной функции? Практическая работа № 3 «Раскрытие неопределенностей. Правило Лопиталя» Цель работы: Научится раскрывать неопределенности с помощью правила Лопиталя. Теоретическая часть (Лопиталь (1661-1704) – французский математик) К разряду неопределенностей принято относить следующие соотношения:
Теорема (правило Лопиталя). Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g¢(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при х®а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.
Аналогично можно применить правило Лопиталя при раскрытии неопределенности
Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат. Естественно, это возможно только в том случае, если вновь полученные функции в свою очередь удовлетворяют требованиям теоремы Лопиталя. Практическая часть Пример 1: Найти предел Решение. Как видно, при попытке непосредственного вычисления предела получается неопределенность вида f¢(x) = 2x +
Пример 2: Найти предел Решение. Числитель и знаменатель при х=0 равны нулю, т.е. имеем неопределенность
Пример 3: Найти предел Решение.
- получили неопределенность. Применяем правило Лопиталя еще раз.
Пример 4: Найти предел Решение. Здесь имеем неопределенность вида
Пример 5: Найти предел Решение. В данном примере имеется неопределенность вида
Практические задания Найдите пределы, используя правило Лопиталя.
Контрольные вопросы:
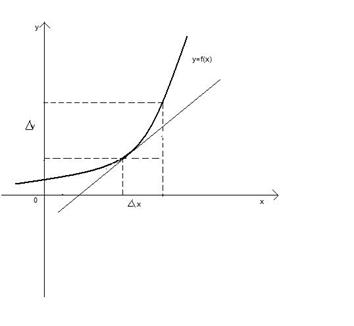
Практическая работа №4 «Дифференциал функции. Приближенные вычисления » Цель работы: Научится находить дифференциал функции. Находить приближенные значения функции с помощью дифференциала». Теоретическая часть Пусть функция y = f(x) имеет производную в точке х:
Тогда можно записать: Следовательно: Величина aDx- бесконечно малая более высокого порядка, чем f¢(x)Dx, т.е. f¢(x)Dx- главная часть приращения Dу. Определение. Дифференциалом функции f(x) в точке х называется главная линейная часть приращения функции. Обозначается dy или df(x). Из определения следует, что dy = f¢(x)Dx. Для функции х производная равна 1, и потому ее дифференциал равен ∆х, dy = f¢(x)dx. (1)
Можно также записать:
Свойства дифференциала. Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:
1) d(u ± v) = (u ± v)¢dx = u¢dx ± v¢dx = du ± dv 2) d(uv) = (uv)¢dx = (u¢v + v¢u)dx = vdu + udv 3) d(Cu) = Cdu 4) 5) С помощью дифференциала можно найти приближенные значения функции. Учитывая, что
Это означает, что приближенное значение функции вблизи точки х0 равно сумме ее значения в этой точке и дифференциала в этой же точке.
Практическая часть. Пример1. Найдите дифференциал функции: а) в) Решение. а) Воспользуемся формулой (1) dy = f¢(x)dx.
б) в) Пример2. Вычислить приближённо: а) 2,0025; б) Решение. а) Воспользуемся формулой (2): Положим 2,002=2+0,002, т.е.
Т.о. б) В данном случае
в) Рассмотрим функцию
Т.о.
Практические задания
Контрольные вопросы
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 482; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.32.230 (0.083 с.) |

 ,
, 


 , (ctgx)/= -
, (ctgx)/= -  ,
, 
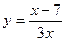 ; в) у=(x4-5x3+7)5
; в) у=(x4-5x3+7)5
 . В нашем случае u= x4-5x3+7
. В нашем случае u= x4-5x3+7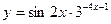 .
.
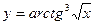 .
.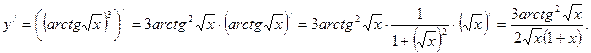
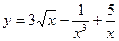 3) y=3x2∙43x.
4)
3) y=3x2∙43x.
4)  5)
5) 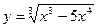 6) y= (x3-4x4+21x)5.
7)
6) y= (x3-4x4+21x)5.
7) 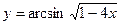 8)
8) 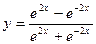
 3)
3)  4)
4) 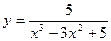 5)
5) 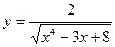 6) y= 2(3x2-x6+5)4.
7)
6) y= 2(3x2-x6+5)4.
7) 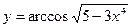 8)
8) 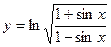
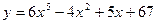 2)
2)  3)
3) 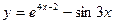 4)
4) 
 5)
5) 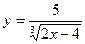 6)
6)  7)
7)  8)
8) 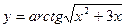
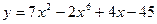 2)
2) 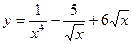 3)
3)  4)
4) 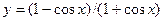 5)
5)  6)
6) 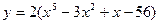 7)
7) 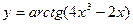 8)
8) 
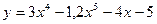 2)
2) 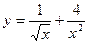 3)
3) 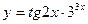 4)
4) 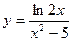 5)
5) 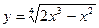 6)
6) 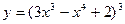 7)
7) 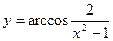 8)
8) 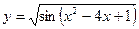
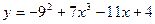 2)
2)  3)
3) 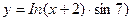 4)
4)  5) y=
5) y= 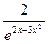 .
6)
.
6) 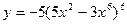 7)
7) 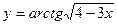 8)
8) 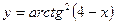 .
.
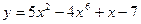 2)
2)  3)
3) 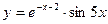 4)
4)  5)
5) 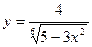 6)
6) 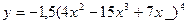 7)
7)  8)
8) 
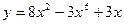 2)
2) 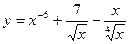 3)
3) 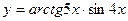 4)
4) 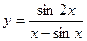 5)
5)  6)
6)  7)
7) 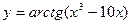 8)
8) 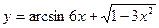
 2)
2) 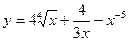 3)
3)  4)
4) 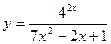 5)
5)  6)
6) 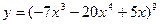
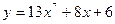 2)
2)  3)
3) 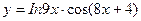 4)
4)  5)
5)  .
6)
.
6) 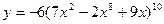
 8)
8) 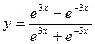 .
.
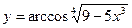 8)
8) 
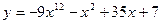 2)
2) 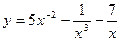 3)
3) 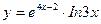 4)
4)  5)
5)  6)
6) 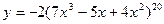 7)
7)  8)
8) 
 2)
2) 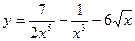 3)
3) 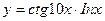 4)
4)  5)
5) 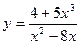 6)
6)  7)
7)  8)
8) 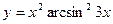
 2)
2) 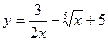 3)
3)  4)
4) 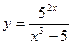 5)
5)  6)
6) 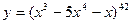 7)
7) 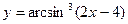 8)
8) 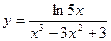
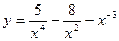 3) y=e5x∙sin(x-5).
4)
3) y=e5x∙sin(x-5).
4) 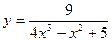 5)
5) 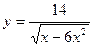 6) y= -5,5(9x2-7x6+1)14.
6) y= -5,5(9x2-7x6+1)14. 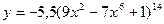 7)
7)  8)
8) 

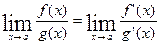
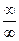 .
.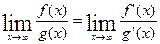
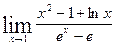
 . Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя.
. Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя. ; g¢(x) = ex;
; g¢(x) = ex;
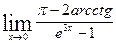
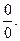
 ;
; 
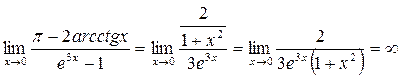

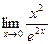
 ,
, 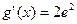 .
.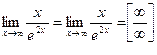
 ,
, 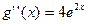 , тогда имеем:
, тогда имеем: 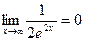
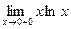
 . Для решения и таких пределов можно применить правило Лопиталя, предварительно сведя ее к неопределенности
. Для решения и таких пределов можно применить правило Лопиталя, предварительно сведя ее к неопределенности 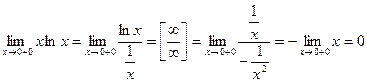
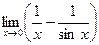
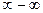 . И здесь можно применит правило Лопиталя, сведя ее к виду
. И здесь можно применит правило Лопиталя, сведя ее к виду 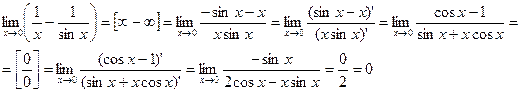
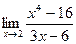 2.
2. 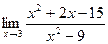 3.
3. 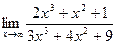 4.
4. 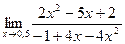
 5.
5.  6.
6. 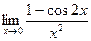 7.
7. 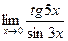 8.
8. 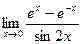 9.
9.  10.
10. 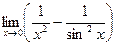
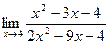 2.
2.  3.
3. 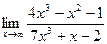 4.
4. 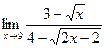 5.
5.  6.
6. 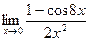 7.
7.  8.
8. 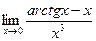 9.
9. 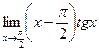 10.
10. 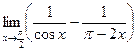
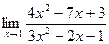 2.
2.  3.
3. 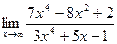 4.
4. 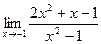 5.
5.  6.
6.  7.
7. 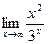 8.
8.  9.
9.  10.
10. 
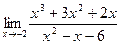 2.
2.  3.
3.  4.
4. 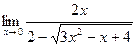 5.
5. 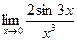 6.
6. 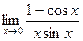 7.
7. 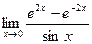 8.
8. 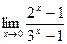 9.
9. 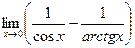 10.
10. 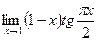
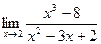 2.
2. 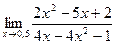 3.
3. 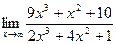 4.
4. 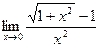 5.
5.  6.
6. 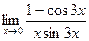 7.
7. 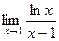 8.
8. 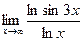 9.
9.  10.
10. 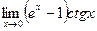
 2.
2. 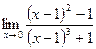 3.
3.  4.
4.  5.
5. 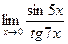 6.
6. 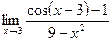 7.
7.  8.
8. 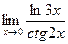 9.
9.  10.
10. 
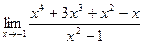 ;
2.
;
2. 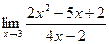 ;
3.
;
3. 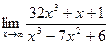 ;
4.
;
4.  5.
5. 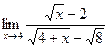 ;
6.
;
6.  ;
7.
;
7. 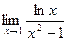 ;
8.
;
8. 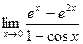 ;
9.
;
9. 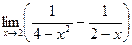 ;
10.
;
10. 
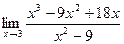 .
2.
.
2.  ;
3.
;
3. 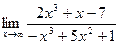 ;
4.
;
4.  ;
6.
;
6. 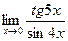 7.
7.  ;
8.
;
8. 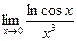 ;
9.
;
9.  ;
10.
;
10. 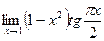
 .
2.
.
2. 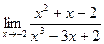 ;
3.
;
3.  ;
4.
;
4.  ;
5.
;
5.  ;
7.
;
7.  8.
8. 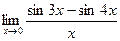 ;
9.
;
9. 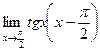 10.
10. 
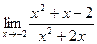 .
2.
.
2. 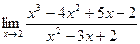 3.
3. 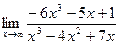 4.
4. 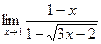 5.
5.  6.
6. 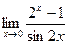 7.
7. 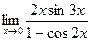 8.
8. 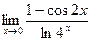 ;
9.
;
9. 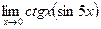 ;
10.
;
10. 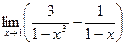
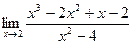 .
2.
.
2. 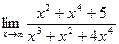 4.
4.  5.
5. 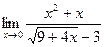 ;
6.
;
6. 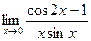 7.
7. 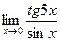 8.
8.  ;
9.
;
9. 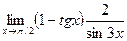 10.
10. 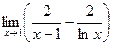
 .
2.
.
2. 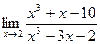 3.
3. 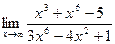 4.
4. 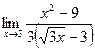 ;
5.
;
5. 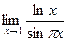 6.
6.  7.
7. 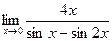 8.
8. 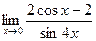 ;
9.
;
9. 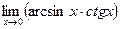 10.
10. 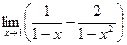
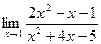 .
2.
.
2. 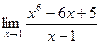 3.
3. 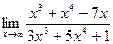 4.
4. 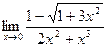 ;
5.
;
5. 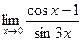 ;
6.
;
6. 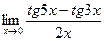 ;
7.
;
7. 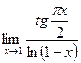 ;
8.
;
8. 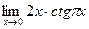 9.
9. 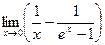 ;
10.
;
10. 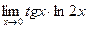
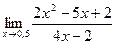 .
2.
.
2.  3.
3.  4.
4. 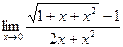 5.
5. 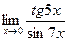 ;
6.
;
6. 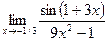 ;
7.
;
7. 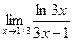 ;
8.
;
8. 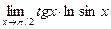 ;
9.
;
9.  ;
10.
;
10. 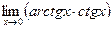

 , где a®0, при Dх®0.
, где a®0, при Dх®0. .
.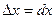 . Поэтому принято вместо
. Поэтому принято вместо 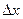 писать dx.. При этом формула дифференциала функции принимает вид:
писать dx.. При этом формула дифференциала функции принимает вид:


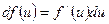 где
где 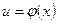 .
. , приращение функции
, приращение функции 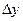 приближённо равно ее дифференциалу, т.е. ∆y»dy, откуда
приближённо равно ее дифференциалу, т.е. ∆y»dy, откуда
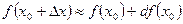 (2)
(2)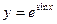 ; б)
; б) 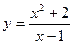 ;
;



 ; в)
; в)  .
.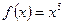 , где х=2,002.
, где х=2,002.



 .
.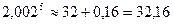 .
. ,
, 
 ;
;
 ;
;
 .
.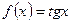 . Полагая х0=450,
. Полагая х0=450,  , имеем:
, имеем: ,
, 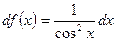 ,
,  .
. .
. в точке
в точке  б)
б)  в)
в) 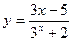 2. Найдите абсолютную и относительную погрешности при замене приращения функции у=2х2+3х ее дифференциалом в точке х=2 при ∆х=0,1.
3. Вычислить приближенно:
а)
2. Найдите абсолютную и относительную погрешности при замене приращения функции у=2х2+3х ее дифференциалом в точке х=2 при ∆х=0,1.
3. Вычислить приближенно:
а)  ;
б) sin440.
;
б) sin440.
 в точке
в точке  б)
б)  в)
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=х2-4х ее дифференциалом в точке х=1 при ∆х=0,1.
3. Вычислить приближенно:
а) 2,0035
2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=х2-4х ее дифференциалом в точке х=1 при ∆х=0,1.
3. Вычислить приближенно:
а) 2,0035  в точке
в точке  б)
б)  в)
в) 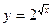 2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=-x3+3х ее дифференциалом в точке х=1 при ∆х=0,01.
3. Вычислить приближенно:
а)3,9923;
б) tg440.
2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=-x3+3х ее дифференциалом в точке х=1 при ∆х=0,01.
3. Вычислить приближенно:
а)3,9923;
б) tg440.
 в точке x=2
б)
в точке x=2
б)  в)
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=-х2-4х ее дифференциалом в точке х=3 при ∆х=0,02.
3. Вычислить приближенно:
а)
2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=-х2-4х ее дифференциалом в точке х=3 при ∆х=0,02.
3. Вычислить приближенно:
а)  ;
б) arctg1,005.
;
б) arctg1,005.
 в точке x=6
б)
в точке x=6
б)  в)
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции у=2х-х2 ее дифференциалом в точке х=3 при ∆х=0,02.
3. Вычислить приближенно:
а)4,953;
б) sin310.
2. Найдите абсолютную и относительную погрешности при замене приращения функции у=2х-х2 ее дифференциалом в точке х=3 при ∆х=0,02.
3. Вычислить приближенно:
а)4,953;
б) sin310.
 в точке x=2
б)
в точке x=2
б)  в)
в)  Найдите абсолютную и относительную погрешности при замене приращения функции у=4х+х2 ее дифференциалом в точке х=4 при ∆х=0,01.
2. Вычислить приближенно:
а)
Найдите абсолютную и относительную погрешности при замене приращения функции у=4х+х2 ее дифференциалом в точке х=4 при ∆х=0,01.
2. Вычислить приближенно:
а)  ;
б) arcctg1,030.
;
б) arcctg1,030.
 в точке
в точке 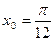 б)
б)  в)
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции у=х2+х-1 ее дифференциалом в точке х=3 при ∆х=0,01.
3. Вычислить приближенно:
4. а) 4,0033;
б) ln1,03.
2. Найдите абсолютную и относительную погрешности при замене приращения функции у=х2+х-1 ее дифференциалом в точке х=3 при ∆х=0,01.
3. Вычислить приближенно:
4. а) 4,0033;
б) ln1,03.
 в точке x=-10
б)
в точке x=-10
б)  в)
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции у=х3-x ее дифференциалом в точке х=2 при ∆х=0,03.
3. Вычислить приближенно:
а)
2. Найдите абсолютную и относительную погрешности при замене приращения функции у=х3-x ее дифференциалом в точке х=2 при ∆х=0,03.
3. Вычислить приближенно:
а)  ;
б) cos610.
;
б) cos610.
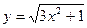 в точке x=4.
б)
в точке x=4.
б)  в)
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции у=х2+х-1 ее дифференциалом в точке х=3 при ∆х=0,04.
3. Вычислить приближенно:
а)
2. Найдите абсолютную и относительную погрешности при замене приращения функции у=х2+х-1 ее дифференциалом в точке х=3 при ∆х=0,04.
3. Вычислить приближенно:
а)  ;
б) sin620.
;
б) sin620.
 в точке x=3
б)
в точке x=3
б)  в)
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=5x-x ее дифференциалом в точке х=2 при ∆х=0,1.
3. Вычислить приближенно:
а)
2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=5x-x ее дифференциалом в точке х=2 при ∆х=0,1.
3. Вычислить приближенно:
а)  ;
б) arctg0,9930.
;
б) arctg0,9930.
 в точке x=4
б)
в точке x=4
б)  2. в)
2. в) 
 ;
б) sin470.
;
б) sin470.
 в точке x=4
б)
в точке x=4
б) 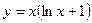 в)
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции у=х2+3х ее дифференциалом в точке х=3 при ∆х=0,03.
3. Вычислить приближенно:
а)
2. Найдите абсолютную и относительную погрешности при замене приращения функции у=х2+3х ее дифференциалом в точке х=3 при ∆х=0,03.
3. Вычислить приближенно:
а)  ;
б) ln1,060.
;
б) ln1,060.
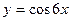 в точке
в точке 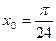 б)
б)  в)
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=-x+x3 ее дифференциалом в точке х=4 при ∆х=0,03.
3. Вычислить приближенно:
а)
2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=-x+x3 ее дифференциалом в точке х=4 при ∆х=0,03.
3. Вычислить приближенно:
а)  ;
б) sin870.
;
б) sin870.
 в точке x=3
б)
в точке x=3
б) 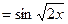 н
в)
н
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=-x3+2x ее дифференциалом в точке х=2 при ∆х=0,1.
3. Вычислить приближенно:
а)
2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=-x3+2x ее дифференциалом в точке х=2 при ∆х=0,1.
3. Вычислить приближенно:
а) 


