
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Роль производных в приближенных вычисленияхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Когда функцию f (x) и ее производную f' (x) легко вычислить при х=а, а для значений х, близких к а, вычисление функции затруднительно, при грубых вычислениях при малых D х пользуются формулой f(x0+ D x)~f(x0)+f' (x 0)D x, не заботясь о величине погрешности. Погрешность для этой формулы можно оценить с помощью значения второй производной (если она, конечно, существует).
Производная и скорость изменения функции. Скачок производной Численное значение производной характеризует скорость изменения функции. На участках, на которых функция меняется быстрее, значение производной больше, чем на тех участках, где функция меняется медленнее (рис. 12). Если аргументом является время, а функция означает пройденный за это время путь, то производная (скорость изменения функции) – это скорость движения.
На рисунке 13 показана функция, у которой в некоторой точке производная не существует. В качестве примера мы взяли функцию, состоящую из 2-х кусков прямых, имеющих разные углы наклона k1 и k2. Уравнение этой функции можно задать следующим образом:
Тогда в точке х=0 В архитектуре при сопряжении двух линий используются оба вида сопряжений – с изломом и без излома. Угол, который образуют друг с другом сопрягающиеся линии, - это угол между касательными к ним. Если правая и левая касательная совпадают, то получается сопряжение гладкое, без излома. Если касательные пересекаются под углом – сопряжение гладким не будет. Таким образом, дуга окружности имеет гладкое сопряжение с касательной, проведенной в конечной точке дуги (рис.15), и сопрягается с изломом с прямой, не являющейся касательной (рис. 16). На рисунке 17 арка из 2-х дуг окружностей имеет излом в верхней точке. При построении сопряжения 2-х дуг окружностей пользуются тем, что касательная к окружности перпендикулярна радиусу, проведенному из центра окружности в точку касания. Следовательно, центры обеих окружностей, дуги которых сопрягаются без излома, должны лежать на одном и том же перпендикуляре к общей касательной. На рисунке 18 приведен чертеж маковки, состоящей из 3-х дуг разных радиусов. Центры окружностей соприкасающихся дуг лежат на одной прямой – О1О2 и О2О3.
Знак производной и монотонность функции. Обращение производной в ноль На участках монотонности функции знак производной сохраняется. Если функция возрастает, то производная положительна (вернее неотрицательна, то есть f'(x)³0), если убывает, то отрицательна (f'(x)£0 - неположительна) - рисунки 19-21. Обращение производной в некоторой точке х=с в ноль может означать следующее.
Если f'(c)=0 и при переходе аргумента слева направо через точку х=с производная f'(x): а) меняет знак с плюса на минус, то точка х=с является точкой максимума (рис. 19), б) меняет знак с минуса на плюс, то точка х=с является точкой минимума (рис. 20), в) не меняет знака, то х=с не является точкой экстремума (максимума или минимума) (рис. 21). Примеры 1. у=х3, y'=3x2. Точка, в которой y '=0 только одна, х =0. Производная – парабола, в окрестности точки х=0 положительна, знака не меняет, следовательно, точка х =0 не является точкой экстремума (рис. 22). Так как производная положительна на всей прямой, функция у=х3 монотонно возрастает на всей прямой.
С помощью нахождения экстремума функции решаются многие задачи, имеющие важное значение на практике и, конечно, в архитектуре. В качестве примера рассмотрим решение некоторых задач по определению оптимальных размеров фигур в пространстве и на плоскости.
Задачи 1. Из всех прямоугольников данной площади S определить тот, периметр которого наименьший (то есть для заданной площади найти форму прямоугольника, требующую минимальных затрат на стены). Ответ. Наименьший периметр имеет квадрат. 2. Из круглого бревна диаметра d вытесывается балка с прямоугольным поперечным сечением, стороны которого равны b и h. При каких размерах балка будет иметь наибольшую прочность, если прочность пропорциональна bh2 (горизонтальная сторона равна b, вертикальная h)?
Ответ. Сечение балки – нормальный прямоугольник (это знали еще древние мастера). Для того чтобы сделать разметку на бревне, надо вырезать из доски "нормальный" прямоугольник, распилить его по диагонали и приложить получившийся треугольник к торцу бревна так, чтобы вершина острого угла лежала на окружности торца, а гипотенуза треугольника шла вдоль диагонали торца бревна. 3. Тело представляет собой прямой круговой цилиндр, завершенный сверху полушаром. При каких линейных размерах это тело будет иметь наименьшую полную поверхность, если объем его равен V? Ответ. Высота цилиндра h равна его радиусу r (такие пропорции имеет Римский Пантеон). 4. При каких линейных размерах закрытая цилиндрическая банка данной вместимости V будет иметь наименьшую полную поверхность (то есть для данного объема найти форму консервной банки, ведра с крышкой и т.д., для которых расход материала будет минимальным). Ответ. Оптимальные размеры имеет банка, у которой высота равна диаметру. Приведем решения этих задач. Задача 1 Обозначим длину прямоугольника через х, а ширину через у, периметр через Р. Тогда S = xy, P =2(x+y). Так как S задано, можно выразить у через х и S: y=S/x и Р=2(х+S/x)=Р(х). Таким образом, надо найти min P(x). Для этого вычислим производную Р(х) и найдем ее нули. P'(x)= 2(1- S/x2), 1- S/x2 =0, S/x2 =1, x2=S, Задача 2 Так как диаметр бревна является диагональю прямоугольного сечения балки, имеющего стороны b и h, согласно теореме Пифагора имеем: d2=b2+h2. Выразим h через b и d: h2=d2-b2. Подставим это выражение в функцию прочности Р и продифференцируем ее по b: P(b)=cb(d2-b2), P'(b)=cd2-3cb2, cd2-3cb2=0 в точке b2=d2/3. Знак производной меняется с плюса на минус, то есть в этой точке достигается абсолютный максимум. h2=d2-b2=d2- d2/3=d22/3 Таким образом, наибольшую прочность имеет балка со сторонами: b=d и оптимальное сечение балки – нормальный прямоугольник. Задача 3 S=2prh+pr2+2pr2=3pr2+2prh, V=pr2h+2/3×pr3 Представим переменную h в виде h=r+a и выразим переменную а через r и V и продифференцирум фунцию S по переменной r. V=5/3×pr3+×pr2a, S(r)=5pr2+2pra=5pr2+2/r×V-10/3×pr2=2V/r+5/3pr2 S'(r)=-2V/r2+2×5/3×pr=r(10/3∙π-2V/r3), S'(r)=0, если V=5/3×pr3, то есть Задача 4 Обозначим через r радиус банки, через h ее высоту, через S ее полную поверхность. Тогда: V=pr2h, S=2pr2+2prh Выразим h через V: h=V/pr2 и подставим в выражение для S: S=2pr2+2V/r=S(r) Вычислим производную S(r) по r и найдем ее нули: S'(r)=4pr-2V/r2=r(4π-2V/r3), 4p-2V/r3=0, r3=V/2p,
Производная в окрестности точки h=2r=d меняет знак с минуса на плюс, следовательно, когда высота цилиндра h равна его диаметру d, величина поверхности банки достигает минимума. Таким образом, оптимальные размеры имеет консервная банка или ведро с крышкой, у которых высота равна диаметру.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1548; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.90.193 (0.008 с.) |

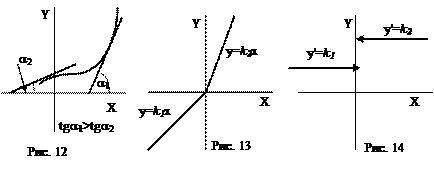

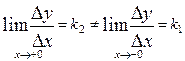 существуют так называемые правая и левая производные (определяемые, как предел отношения приращения функции к приращению аргумента справа и слева, соответственно), но они не равны друг другу и поэтому производная в этой точке не определена. На графике функции в таких точках виден "излом", а производная функция y' в этой точке имеет разрыв I рода (рис. 14).
существуют так называемые правая и левая производные (определяемые, как предел отношения приращения функции к приращению аргумента справа и слева, соответственно), но они не равны друг другу и поэтому производная в этой точке не определена. На графике функции в таких точках виден "излом", а производная функция y' в этой точке имеет разрыв I рода (рис. 14).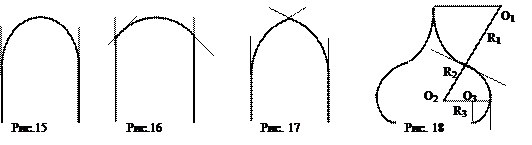

 2. y =cosx, y '=-sinx. Возможными точками экстремумов являются все точки, в которых sin x =0 (х =±kp, k=0, 1, 2, 3,…). И во всех таких точках производная меняет знак, то есть они все являются точками локальных экстремумов (рис. 23).
2. y =cosx, y '=-sinx. Возможными точками экстремумов являются все точки, в которых sin x =0 (х =±kp, k=0, 1, 2, 3,…). И во всех таких точках производная меняет знак, то есть они все являются точками локальных экстремумов (рис. 23).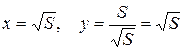 . Легко видеть, что знак производной в этой точке меняется с минуса на плюс, производная строго возрастает и в этой точке достигается абсолютный минимум. Тем самым, мы доказали, что наименьший периметр имеет квадрат.
. Легко видеть, что знак производной в этой точке меняется с минуса на плюс, производная строго возрастает и в этой точке достигается абсолютный минимум. Тем самым, мы доказали, что наименьший периметр имеет квадрат. , h=d
, h=d  =
=  b
b ,
, , a=0,производная в окрестности точки h=r меняет знак с минуса на плюс, и, следовательно, когда высота цилиндра h равна его радиусу r, величина поверхности достигает абсолютного минимума (такие пропорции имеет Римский Пантеон).
, a=0,производная в окрестности точки h=r меняет знак с минуса на плюс, и, следовательно, когда высота цилиндра h равна его радиусу r, величина поверхности достигает абсолютного минимума (такие пропорции имеет Римский Пантеон). ,
,



