
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эксцентриситет эллипса и параболыСодержание книги
Поиск на нашем сайте
Начертить эллипс очень просто и без циркуля и линейки. Для этого вам надо взять кусок картона, воткнуть в него две булавки на некотором расстоянии друг от друга. Точки, в которые воткнуты булавки, – это фокусы будущего эллипса. Затем надо взять нитку длины большей, чем расстояние между булавками, и привязать концы нитки к булавкам. Внутрь петли, образованной ниткой, вставьте карандаш, отведите его от булавок так, чтобы нитка натянулась, поставьте отточенный конец карандаша на картон, затем аккуратно обведите карандаш вокруг булавок. Когда рисуемый вами овал замкнется, эллипс готов (рис. 11). Способ, которым вы получили эту кривую, вам гарантирует, что сумма расстояний от любой ее точки до фокусов для всех точек одинакова – она равна длине нити. Выбирая разные фокусные расстояния и разную длину нитки, вы получите эллипсы большего или меньшего размера, вытянутые в длину или похожие на окружность (рис. 12). Рамка, имеющая форму эллипса Число называется эксцентриситетом эллипса. В силу того, что a>c, это отношение всегда меньше единицы (e<1). При с =0, когда эллипс вырождается в окружность, эксцентриситет равен нулю. Из формулы для b видно, что чем ближе эксцентриситет к единице, тем ближе к нулю отношение b/ а, и тем меньше эллипс напоминает окружность (рис. 12). Для орбиты Земли e=0,017.
Можно рассматривать параболу, как "предел эллипсов", когда один из фокусов стремится в бесконечность. А именно, если эллипс растягивать так, чтобы один из его фокусов оставался на месте, а другой стремился в бесконечность, то эллипс будет стремиться обратиться в параболу, а эксцентриситет эллипса будет стремиться к 1. Эксцентриситет параболы равен 1. Эллипс – фигура, часто встречающаяся в природе. Например, если наклонить стакан с водой, то очертание верхнего слоя воды будет эллипсом. (Рис 13а). Еще Кеплер обнаружил, что планеты движутся вокруг Солнца не по кругам, а по эллипсам. Солнце находится в фокусе каждого эллипса (рис 13б). Фокусы эллипса обладают замечательным свойством. Если изогнуть узкую полоску металла по дуге эллипса и поместить источник света в одном фокусе, то лучи света, отразившись от полоски, соберутся в другом фокусе (рис 14). В комнате с эллипсоидным потолком слова, сказанные шепотом человеком, стоящим в одном из фокусов, хорошо слышны человеку, стоящему в другом фокусе (так называемые комнаты "шепотов").
Примеры 1. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и большая ось равна 10. Решение. Из условия задачи 2 с =8, 2 а =10, следовательно: с =4, а =5, b 2= a2-c2 =25-16=9 и уравнение эллипса: 2. Определить фокусы и эксцентриситет эллипса: Решение. Из уравнения эллипса находим оси эллипса: а =5, b =13. Так как b>a, эллипс вытянут вдоль оси Y. И фокусы расположены на оси Y. Фокусное расстояние с связано с осями эллипса соотношениями: b2=a2-c2 для эллипса, вытянутого вдоль оси Х, и а2=b2 - c 2 для эллипса, вытянутого вдоль оси Y. Отсюда с2=b2-a2 =169-25=144, то есть
3. Выберите произвольную точку на эллипсе Решение. Пусть (х0, у0) - точка, лежащая на эллипсе. Симметричная ей точка относительно оси Y (- х0, у0), относительно оси Х (х0, -у0), относительно начала координат (- х0, -у0). Они тоже лежат на эллипсе, так как в уравнении эллипса содержатся только квадраты координат, а координаты симметричных точек отличаются только знаком. Чтобы подобрать координаты конкретной точки, лежащей на эллипсе, надо взять любое значение х <5, например, х =3, подставить это значение в уравнение эллипса и определить 2 значения у, соответствующих этому значению х:
Конические сечения
Если рассечь конус плоскостью так, чтобы разрез проходил через основание конуса, можно получить в сечении дугу параболы или дугу гиперболы. Окружность можно получить, рассекая круговой цилиндр или круговой конус горизонтальной плоскостью. Таким образом, все кривые – и эллипс, и гипербола, и парабола являются коническими сечениями. Пересечение плоскостью двустороннего конуса, простирающегося в бесконечность, дает бесконечную параболу и бесконечную гиперболу (рис. 15). На чертеже хорошо видно, как меняется сечение с изменением угла наклона секущей плоскости. Когда плоскость горизонтальна – это окружность. Начинаем вращать плоскость - окружность обращается во все более вытянутый эллипс. То есть эксцентриситет растет, и из нулевого становится все больше похожим на единицу. Когда плоскость становится параллельной касательной плоскости конуса, второй фокус эллипса улетает в бесконечность и эллипс обращается в параболу, эсцентриситет которой равен 1. Продолжаем плавно изменять угол наклона секущей плоскости. Она начинает рассекать еще и верхнюю часть конуса. Кривая обращается в гиперболу с двумя ветвями. Горизонтальная плоскость, проходящая через вершину конуса, пересекает конус по точке. Если пересечь конус вертикальной плоскостью, проходящей через вершину конуса, получатся две пересекающиеся прямые. Одна прямая получится, если секущая плоскость проходит через образующую (ребро) конуса. Две параллельные – если рассечь вертикальной плоскостью бесконечный цилиндр. Цилиндр можно представить себе, как конус с бесконечно удаленной вершиной. Коническим сечением станут параллельные прямые. Все рассуждения сохраняются и для не прямого (наклонного) кругового конуса. Вследствие всего сказанного эллипсы, гиперболы и параболы называются коническими сечениями (кониками), хотя, как мы видели, набор конических сечений много богаче. Кривые второго порядка Общее уравнение второго порядка относительно х и у содержит члены второй степени – х2, ху, у2, первой степени – х, у и нулевой степени (свободный член), а значит имеет вид: A х 2+B xy +C у 2+D x +E y +F=0. Здесь хотя бы один коэффициент А, В, С должен быть отличен от нуля. Представленное уравнение является уравнением второй степени, а линии, уравнения которых описываются таким уравнением, называются кривыми второго порядка. В аналитической геометрии доказывается, что уравнение второй степени самого общего вида задает или эллипс, или гиперболу, или параболу, или пару прямых, или одну точку, или вообще задает пустое множество, то есть является уравнением конического сечения. Доказательства проводятся средствами линейной алгебры. Кривые второго порядка отвечают высоким эстетическим требованиям. Их часто применяют как в технических формах, так и в архитектуре. Например, кривая контура части монумента Покорителям Космоса в Москве была прорисована архитекторами "от руки", затем для инженерных расчетов с помощью ЭВМ было найдено уравнение чертежа: 0,314х2-2×1,287xy-y2+2×30,259x+289,982y-6528,191=0 (мы оставили только 3 знака после запятой).
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 867; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.205.182 (0.009 с.) |

 , где а - большая полуось, а с – фокусное расстояние,
, где а - большая полуось, а с – фокусное расстояние,

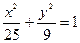

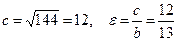 и координаты фокусов; F1(0,-12), F2(0,12).
и координаты фокусов; F1(0,-12), F2(0,12). и укажите симметричные ей точки относительно осей и начала координат. Принадлежат ли они эллипсу?
и укажите симметричные ей точки относительно осей и начала координат. Принадлежат ли они эллипсу?
 На примере стакана с водой мы видели, как просто получить эллипс. Вообще, если прямой цилиндр разрезать наискось так, чтобы не затронуть при этом оснований, то в разрезе получится эллипс. И если такую операцию проделать с конусом, то тоже получится эллипс.
На примере стакана с водой мы видели, как просто получить эллипс. Вообще, если прямой цилиндр разрезать наискось так, чтобы не затронуть при этом оснований, то в разрезе получится эллипс. И если такую операцию проделать с конусом, то тоже получится эллипс.


