
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выпуклые, вогнутые и кровли с перегибомСодержание книги
Поиск на нашем сайте
Рассмотрим различные формы кровель (куполов, маковок) с точки зрения выпуклости и вогнутости их силуэтов и их усложнение по мере развития архитектурных идей. Приведем схемы главных силуэтов. Самый простой купол - полусфера или ее часть, имеет выпуклую форму (рис. 25а).
В Японии, Китае были распространены вогнутые кровли (рис. 25б). На арабском Востоке приняты выпуклые купола (рис. 25в). На Руси первые маковки имели форму шлема, то есть полусферы (рис. 26а). Позднее "шишак" шлема начали вытягивать вверх, и в отличие от восточных куполов на русских куполах имеется перегиб – центр дуги окружности в точке перегиба "перекидывается" на другую сторону касательной. Самая простая модель для построения маковки циркулем и линейкой – перегиб на длине дуги в 60°, сопряжение дуг в точке перегиба гладкое, то есть сопрягающиеся дуги имеют общую касательную, и центры дуг лежат на одной прямой (рис. 26б). Для усовершенствования формы бока маковки в XVI веке начали раздвигать, центры дуг при этом не лежат на одной прямой и перегиб получается с изломом. На рисунке 26в приведен пример такой маковки (пример взят из журнала "Реставратор", 1999г., вып.10). В точке сопряжения проведены касательные, видно изменение угла наклона касательной при прохождении точки перегиба. На чертеже видны излюбленные мастерами пропорции - в основе построения лежат 4 квадрата со стороной а. Сечение маковки до перегиба вписано в золотой прямоугольник, малая сторона которого равна а. Расстояние от уровня перегиба до креста, венчающего маковку, равно диагонали квадрата со стороной а, сечение барабана – прямоугольник, меньшая сторона которого равна стороне квадрата, большая получается с помощью «золотого» сечения отрезка, равного двум сторонам квадрата, т. е. равна 2j а, где j=0,618 ("двойное золото" 2j»1,236).
В XVIII веке появились маковки очень сложной формы, состоящие из многих дуг и дополнительных крыш с перегибами. Появились даже маковки с целиком вогнутой верхней частью (рис. 26г).
Важным понятием является кривизна дуги. Точное определение кривизны K следующее. Возьмем на кривой две точки – M и N. Проведем касательные к кривой в этих точках и рассмотрим предел отношения угла смежности d между положительными направлениями касательных к длине дуги MN, когда дуга MN®0 (рис. 27). Абсолютную величину этого предела называют кривизной кривой в точке М.
Кривизна линии y=f(x) вычисляется по формуле: Заметим, что в отличие от первой и второй производной кривизна зависит только от формы графика и не зависит от системы координат. В силу этого кривизна является очень важным понятием при изучении формы кривой. Радиусом кривизны R в точке М называют величину, обратную кривизне: Понять, что такое кривизна, помогают следующие простые примеры. 1.Кривизна прямой равна 0. 2.Кривизна во всех точках окружности радиуса R одинаковая, она равна Таким образом, прямую можно рассматривать, как окружность бесконечного радиуса.
Чем больше искривлена кривая вблизи данной точки, тем больше кривизна K и меньше радиус кривизны R в этой точке. Окружность, описанная из центра кривизны С радиусом R=MC, называется соприкасающейся окружностью или кругом кривизны линии L для точки М (рис. 28а). Линия L может располагаться в окрестности точки М как внутри круга кривизны (рис. 28б), так и вне него (рис. 28в). Первый случай имеет место, например, для конца малой оси эллипса, второй – для конца большой его оси. Если при сопряжении двух линий, производные справа и слева в точке сопряжения неодинаковые, производная терпит разрыв, сопряжение получается, как мы уже говорили, негладкое и на графике виден излом. Если при сопряжении двух линий их первые производные в точке сопряжения совпадают, но не совпадают вторые производные, то будет иметь место разрыв кривизны. В ряде задач необходимо обеспечить непрерывность кривизны. Например. Если поворот железной дороги спроектирован как сопряжение прямой и окружности радиуса R (рис. 29), то центростремительное ускорение, равное v2/R, будет в точке сопряжения меняться скачком. Рельсы при этом будут расшатываться. Поэтому, вместо окружности лучше использовать параболу. Например, дорогу можно описать уравнением: y=0 при x<0, у=kx3 при х³0. Для параболы y=kx3 y''=6kx и кривизна при увеличении х сначала постепенно нарастает от нуля до величины, зависящей от коэффициента k, затем начинает убывать. Это позволяет сгладить поворот (на практике закругление железной дороги делают по так называемой клофоиде, по лемнискате Бернулии, из нескольких дуг и т.д.). Чем больше производных совпадает при сопряжении, тем выше уровень гладкости сопряжения.
В архитектуре при сопряжении дуги с прямой часто используют вспомогательные (переходные) дуги. Например, если сечение свода полуокружность, то переход вертикалей в дугу смягчают, создавая многоцентровой свод. На рисунке 30 приведен пример "византийского" многоцентрового свода, на рисунке 31 - применяемого на Руси так называемого "крутопятого" свода (примеры взяты из журнала "Реставратор", 2001г., №1). На рисунке 32 приведены графики величины радиуса кривизны, (сама линия дана сплошной чертой, график радиуса кривизны - штриховой). Второй чертеж демонстрирует метод сглаживания кривизны. Эволютой данной кривой называется кривая, состоящая из центров кривизны для всех точек данной кривой. Эволюта прямой состоит из одной бесконечно удаленной точки. Так что в первом примере эволюта состоит из бесконечно удаленной точки и центра дуги окружности О. Во втором примере, кроме бесконечно удаленной точки, центров кривизны уже 2 - О1 и О2. В последнем примере эволюта состоит из 2-х точек - О1 и О2. У кривых, обладающих гладкой кривизной, эволюта - это линия.
На рисунке 33 приведен график эволюты эллипса. Этот график позволяет понять, чем отличается овал, имитирующий эллипс, имеющий 4 центра кривизны (на рис. 33 они отмечены жирными точками – см. рис. 5 гл.9), от настоящего эллипса.
Задачи для самостоятельного решения 1. Каковы должны быть стороны прямоугольного участка, периметр которого равен 120м, чтобы площадь этого участка была наибольшей? 2. Прямоугольный участок земли площадью 4га огораживается забором. Каковы должны быть размеры сторон участка, чтобы забор имел наименьшую длину? 3. Построить из дуг окружностей разрез одноцентровой маковки с перегибом на шестидесятой параллели. Сопряжение дуг гладкое. 4. Начертите эскиз двуцентровой маковки. 5. Сравнить 2 способа проектирования поворота железной дороги - сопряжение прямой и параболы y=x3 и сопряжение прямой и окружности радиуса 1. Для этого на отрезке (0, 1) вычислить значения с интервалом 0,1 и построить по точкам графики параболы у1=х3 и окружности х2+(у-1)2=1 (
Какова максимальная разница значений, выраженная в процентах? Пусть радиус закругления железной дороги равен 1км. На сколько метров разойдутся рельсы, имеющие форму такой параболы и окружность радиуса 1км на отрезке длиной в 1км?
Глава 12 Интегральное исчисление Неопределенный интеграл В дифференциальном исчислении решается задача: по данной функции найти ее производную. В интегральном исчислении решается обратная задача: дана функция f(x), которая является производной функцией некоторой функции F(x), и по функции f(x) будем искать ее первообразную F(x). Первообразной функцией для данной функции f(x) называется функция F(x), производная которой равна f(x), или дифференциал которой равен f(x)dx, то есть F'(x)=f(x), или dF(x)=f(x)dx. Так, например, для функции f(x)=3x2 первообразной будет F(x)=x3, так как (x3)'=3x2 то есть F'(x)=f(x). Не всякая функция f(x) имеет первообразную, но если, например, функция f(x) – непрерывна на интервале, то она имеет на нем первообразную. Задача отыскания по данной функции ее первообразной решается неоднозначно. Например, функция F(x)=x3 есть первообразная для f(x)=3x2, но функция F1(x)=x3+5 также будет первообразной для 3x2, так как F'1(x)=(x3+5)'=3x2. Вообще любая функция x3+с, где с – произвольная постоянная, имеет производную 3x2 и потому будет первообразной для 3x2. Выражение: F(x)+c представляет собой общий вид первообразных для f(x). Совокупность всех первообразных называется неопределенным интегралом функции f(x) и обозначается:
Отыскание неопределенного интеграла называют интегрированием функции f(x). Если функцию f(x) проинтегрировать, а затем продифференцировать, то получим снова функцию f(x). Действительно, так как (F(x)+c)'=f(x), то Таким образом, дифференцирование и интегрирование являются взаимно обратными операциями. Перечислим основные свойства неопределенного интеграла. 1. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме неопределенных интегралов, то есть:
2. Постоянный множитель можно выносить за знак интеграла, то есть:
Чтобы проверить эти свойства, достаточно продифференцировать обе части равенства.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 593; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.210.35 (0.007 с.) |





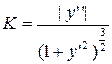
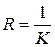 . Центр кривизны находится на нормали к кривой в направлении ее вогнутости на расстоянии R от точки М.
. Центр кривизны находится на нормали к кривой в направлении ее вогнутости на расстоянии R от точки М. . Центром кривизны окружности является центр окружности.
. Центром кривизны окружности является центр окружности.


 ), заполнив для этого таблицу:
), заполнив для этого таблицу:
 .
.




