
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Шары, эллипсоиды, конусы, цилиндры, параболоиды, гиперболоидыСодержание книги
Поиск на нашем сайте
Уравнение шара: x2+y2+z2=a2 - любая плоскость пересекает шар по окружности. Для плоскостей z=h h<a - это окружности x2+y2=а2-h2. Из соображений симметрии это верно и для любой другой плоскости, нормаль к которой можно рассматривать в качестве координатной оси) Уравнение эллипсоида: Уравнение конуса: Цилиндрическая поверхность – поверхность, направляющей которой является кривая второго порядка, например, эллипс или парабола, образующей – вертикальная прямая. То есть цилиндр строится следующим образом. На плоскости XOY рассмотрим кривую второго порядка с уравнением F(x,y)=0. Через каждую точку М(х,у,0) линии проведем прямую, параллельную оси Z. Все эти прямые составят поверхность, которая называется цилиндрической. Тип кривой определяет название цилиндра, например: эллиптический - параболический – y 2=2 px. Плоскость z=h пересекает цилиндр независимо от значения z по одной и той же кривой, уравнение которой от z не зависит. Эллиптический параболоид:
Гиперболоид однополостный:
Гиперболический параболоид: Более подробное описание и рисунки поверхностей второго порядка можно найти в справочниках.
Прямолинейные образующие Прямолинейной образующей называется прямая линия, целиком лежащая на данной поверхности. Поверхность называется линейчатой, если ее можно образовать движением прямой линии (образующей). Из таких образующих состоят конус, цилиндр, плоскости, однополостный гиперболоид и даже седло. Телевизионная башня, состоящая из прямолинейных металлических полос (образующих однополостного гиперболоида), дает нам наглядный пример применения на практике линейчатых свойств криволинейной поверхности. Полосы склепываются в местах пересечения двух систем образующих и при малой затрате материала конструкция обладает большой прочностью. Идея применения в строительной технике конструкции из металлических полос, расположенных так, как расположены прямолинейные образующие однополостного гиперболоида, принадлежала знаменитому русскому инженеру Шухову.
Задачи для самостоятельного решения 1. Постройте график гиперболы. 2. Построить на том чертеже, на котором нарисован график цепной линии (см. задачу 7 гл. 9), по вершине и точке параболу (вершины у обеих линий совпадают, вторая точка параболы лежит на цепной линии). 3. Нарисуйте висящую гирлянду, воспользовавшись для ее линии провиса графиком параболы, заменяющей цепную линию, подобрав масштаб и кусок графика так, чтобы прогиб соответствовал тому, что вы желаете. 4. Постройте эскиз из струй фонтана, имеющих форму парабол. 5. Выберите два произвольных отрезка а и b и постройте на одном чертеже эллипс и овал с выбранными вами полуосями. Отметьте точки фокусов. 6. Постройте изображение шара с экватором и полюсом. 7. Постройте линию, которая получится, если: а) ординаты точек окружности х2+у2 =16 уменьшить в 2 раза, не изменяя абсцисс; б) абсциссы точек окружности х2+у2 =9 уменьшить в 2 раза, не изменяя ординат. Каковы уравнения полученных линий? 8. Определите радиус окружности, сжатием которой к оси Х получен эллипс 9. Составить каноническое уравнение эллипса, если полуоси его соответственно равны 5 и 4. Каковы координаты его фокусов? 10. Определить полуоси эллипсов: а) 25х2+16у2= 1, б) х2+4у2=1 11. Постройте линию, определяемую уравнением: 4х2+9у2 =36 12. Поверхность задана уравнением 13. Поверхность задана уравнением
Глава 11 Непрерывность функции. Производная и кривизна Понятие предела Рассматривая вопрос о сумме бесконечно убывающей геометрической прогрессии, о вычислении длины окружности, площади круга и поверхностей и объемов круглых тел, мы уже пользовались понятием предела. Дадим точное определение предела. Пусть задана бесконечная последовательность чисел a1, a2, a3,…,an,… Если по мере возрастания номера n члены значения членов последовательности приближаются к некоторому числу а так, что абсолютная величина разности | an-a | становится меньше любого наперед заданного числа, то число а называют пределом числовой последовательности an при возрастании аргумента (номера) n. Это кратко записывают так:
Например, Величина an, стремящаяся к 0 при бесконечном возрастании n, называется бесконечно малой. Эти же рассуждения и понятия можно применить и в случае непрерывного аргумента. Примеры 1. Этот предел означает, что при достаточно малых х sin x и х эквивалентны друг другу (напомним, что х – это величина угла, выраженная в радианах) (рис. 1). Это записывают так: sinx~ х Смысл I-го замечательного предела состоит в том, что если центральный угол aрад окружности единичного радиуса мал, то длина а полухорды, стягивающей этот угол, и длина дуги s, на которую угол опирается (рис.2), - величины эквивалентные. Действительно, величина угла в радианах – это и есть длина дуги окружности единичного радиуса, на которую угол опирается. А длина полухорды a =sina). Длину окружности L и вычисляют, как предел периметров вписанных n-угольников, когда число сторон n стремится к бесконечности. Если n велико, то an мало и выполняется sinan/2~an/2 и an ~2Ran/2=Ran=s. Если Ln периметр многоугольника, то Ln=n an ®L.
Алгоритм предельного перехода применяется и для определения площади круга. Площадь круга S есть предел площадей n-угольников Sn. Sn складывается из площадей n треугольников равной площади s, вершиной которых является центр окружности, а основанием – сторона многоугольника (рис. 3). По формуле для вычисления площади треугольника получаем sn=1/2Ran. Sn=nsn=n×1/2R a n=1/2RLn®1/2RL=1/2R×2pR=pR2 Архимед за 2тыс. лет до трудов Лейбница и Ньютона об исчислении бесконечно малых, определивших последующее развитие методов математического анализа в Европе, для определения значения числа p применил идею предельного перехода. Он вычислил периметры вписанных в окружность и описанных около нее правильных многоугольников от 6-ти до 96-ти угольника и определил очень узкие пределы для числа p: 2. II замечательный предел. Этот предел мы уже рассматривали, когда делали оценки величины наращенного вклада, когда число периодов начисления процентов по вкладу велико.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 766; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.78.12 (0.007 с.) |

 - любая плоскость пересекает эллипсоид по эллипсу (на рис. 20 приведен чертеж эллипсоида и других обсуждаемых тел).
- любая плоскость пересекает эллипсоид по эллипсу (на рис. 20 приведен чертеж эллипсоида и других обсуждаемых тел). - вершина конуса в начале координат.
- вершина конуса в начале координат. ,
, - сечения, параллельные плоскости XOY (z=c) – эллипсы (их уравнения
- сечения, параллельные плоскости XOY (z=c) – эллипсы (их уравнения  ), сечения плоскостями XOZ (y=0) и YOZ (x=0) – параболы x2=a2z и y2=b2z и, вообще, сечения, параллельные оси Z – параболы.
), сечения плоскостями XOZ (y=0) и YOZ (x=0) – параболы x2=a2z и y2=b2z и, вообще, сечения, параллельные оси Z – параболы.
 - телевизионная башня Шухова, имеет два семейства прямолинейных образующих (см. ниже).
- телевизионная башня Шухова, имеет два семейства прямолинейных образующих (см. ниже).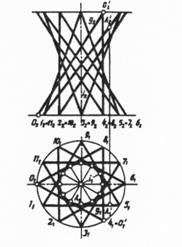

 Двуполостный гиперболоид:
Двуполостный гиперболоид: 
 (так называемое седло)
(так называемое седло) . Каковы координаты фокусов эллипса?
. Каковы координаты фокусов эллипса? . Что представляют собой линии ее пересечения с плоскостями z=0, х=0, у=0?
. Что представляют собой линии ее пересечения с плоскостями z=0, х=0, у=0? . Что представляют собой линии ее пересечения с плоскостями z=0, х=0, у=0?
. Что представляют собой линии ее пересечения с плоскостями z=0, х=0, у=0? или
или  или просто an®a
или просто an®a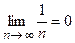 или
или 
 - I замечательный предел.
- I замечательный предел.
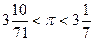 .
.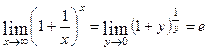 или
или 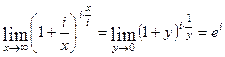 -
-


