
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический смысл производнойСодержание книги Поиск на нашем сайте
а) Геометрический смысл производной. Рассмотрим график функции y=f(x), дифференцируемой в точке x0 (рис. 13). Проведем через точки M0(x0,y0) и M(x0+▲x, y0+▲y) графика прямую l, и пусть B(угол Бэтта) - угол ее наклона к оси х. Тогда (1)▲y/(деленный)▲x=tg B(бэтта)
Рис. 13. Если ▲x стремится к нулю, то ▲y также стремится к нулю, и точка M приближается к точке M0, а прямая l - к касательной l0(эль нулевая), образующей с осью x угол α(альфа). При этом равенство (1) принимает вид: (2) f ’(x0)=tgα’ откуда следует, что производная функции в точке равна тангенсу угла наклона касательной к графику функции в этой точке. Понятие дифференцируемости ф-ии Df: Ф-ия
Dh: Для дифференцирования ф-ии в т. х0, необходимо и достаточно, чтобы в этой точке существовала производная. Доказательство: (необходимость)
(достаточность): Непрерывность и диф. Понятие дифференциала ф-ии. Геом.смысл приблеженных вычислений с помощью dy Опр. Дифференциалом ф-ии y=f(x) в точке х0 н-ся главная, линейная от-но ▲х, часть приращенная ф-ии в этой точке. Для обозначения дифференциала ф-ии используют символ dy. Из Df дифференцируемости следует, что приращение дифф. ф-ии Из равенства нулю предела следует, что Поскольку
Пусть
**************
Zm1: Zm1:
Правила диференц суммы,разн,произв,частн 1) 2) 3) 4) 5) если
где индексы указывают, по какому аргументу производится дифференцирование. 38.Вычислен производных элемент.ф-ий: x^n,nЄN,cos,sin,tg,ctg, loga(основание)Х(а>0,a≠1,x>0) Th о произв сложной ф-ии Пусть: 1. 2. 3. тогда сложная ф-ия
Доказательство: 1. 2.
3.
40.Производная ф-ий x^α, αЄR(прием логарифм. Диф) Th о производной обратной ф-ии Предложение: Если производная обратной функции g для ф-ции f существует в точке y0, то g’(y0)=1/f’(x0), где y0=f(x0) Доказательство: g(f(x))=x g’(f(x))=1 g’(f(x0))=g’(f(x0))*f’(x0)=1, g’(f(x0))=g(y0)=1/f’(x0) Теорема: Пусть ф-ция f строго монотонно и непрерывно отображает (a,b) в (а,b) тогда $ обратная ей ф-ция g, которая строго монотонно и непрерывно отображает (а,b) в (a,b). Если f диф-ма в точке x0Î(a,b) и f’(x0)¹0, то g диф-ма в точке y0=f(x0) и g’(y0)=1/f’(x0) Доказательство: Возьмем произвольную последовательность сходящуюся к y0: yN®y0, yN¹y0 => $ посл-ть xN: xN=g(yN), f(xN)=yN g(yN)-g(y0)/yN-yO = xN-xO/f(yN)-f(yO) = 1/f(yN)-f(yO)/xN-xO ® 1/f’(xo) при n®¥, получили при xN®xO g(yN)-g(yO)/yN-yO®1/f’(xO) => g’(уO)=1/f’(xO) 42.Произв ф-ии: arcsinx,arccosx,arctgx,acctgx,a^x(a>0,a≠1) 1) x®Arcsin x по теореме имеем Arcsin’x=1/Sin’y, где Sin y=x при условии, что Sin’y<0, получаем (используя производную синуса): Arcsin’x=1/Cos y, т.к. Arcsin: [-1,1]®[-П/2,П/2] и Cos:[-П/2,П/2]®[0,1], то Cos y³0 и, значит Arcsin’x = 1/Cos y = 1/(1-Sin2y)1/2 = 1/(1-x2)1/2 2) x®Arccos’x = -1/(1-x2)1/2 3) x®Arctg’x = 1/1+x2 4) x®Arcctg’x= -1/1+x2 5) y=a^x(в степени х) y ‘ =a^xlna Док-во:y=a^x является обратной для ф-ии x=loga(a-основание)y. Т.к. x’(y)=(1/y)loga(a-осн)e, то из соотношения loga(a-OCH)b=1/logb(b-OCH)a получим y’(x)=1/x’(y)=y/loga(a-OCH)e=a^x(в степени х)lna Производная высших порядков Определение: Если ф-ция f диф-ма в некоторой окрестности точки xO, то ф-ция f’(x):x®f’(x) в свою очередь может оказаться диф-мой в точке xO или даже в некоторой ее окрестности. Производная ф-ции f’(x) - называется второй производной (или производной порядка 2) ф-ции f в точке xO и обознача ется f”(x). Аналогично определяется третья и четвертая производная и так далее. Для единообразия обозначаем через fN(xO) - производную порядка n функции f в точке xO и при n=0 считаем f0(xO)=f(xO). Замечание: Cуществование производной порядка n требует того чтобы существовала производная пордка (n-1) уже в некоторой окрестности точки xO (следует из теоремы о связи диф-ти и непрерывности), в таком случае функция x®fN-1(x) непрерывна в точке xO, а при n³2 все производные порядка не выше (n-2) непрерывны в некоторой окрестности точки xO. Пусть функции у=f(х) и х=g(t) таковы, что из них можно составить сложную функцию у=f(g(t)). Если существуют производные у’(х) и х’(t) то cуществует производная у’(t)=у’(х)*х’(t). Пусть функции у=f(х) и х=g(t) таковы, что из них можно составить сложную функцию у=f(g(t)) Если существуют производные у’(х) и х’(t) то существует производная у’(t)=у’(х)*х’(t) +нужно док-во
|
|||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 344; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.242.20 (0.006 с.) |


 дифференцируема в точке х0, если приращение ф-ии в точке сможет быть представлено в виде:
дифференцируема в точке х0, если приращение ф-ии в точке сможет быть представлено в виде: , А – const.
, А – const.

 можно представить в виде
можно представить в виде 
 - б.м. более высшего порядка малости, чем
- б.м. более высшего порядка малости, чем  , и
, и 
 - б.м. одного порядка малости.
- б.м. одного порядка малости. - б.м. одного порядка малости
- б.м. одного порядка малости  - б.м. эквивылентные, т.е.
- б.м. эквивылентные, т.е. 


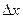 и х – независимые переменные, т.е.
и х – независимые переменные, т.е. 
 для независимых переменных.
для независимых переменных.
 ;
; , где
, где  - постоянная;
- постоянная; ;
; ;
; , а
, а  , то производная сложной функции
, то производная сложной функции  находится по формуле
находится по формуле ,
, - дифф. в точке y0.
- дифф. в точке y0. - дифф. в точке х0.
- дифф. в точке х0.
 - дифф. в точке х0 и справедлива формула:
- дифф. в точке х0 и справедлива формула:
 - дифф. в точке y0
- дифф. в точке y0 
 - дифф. в точке х0
- дифф. в точке х0 

 .
.





