Односторонние производные функции в точке
Похожие статьи вашей тематики
Определение. Правой (левой) производной функции f(x) в точке х = х 0 называется правое (левое) значение предела отношения  при условии, что это отношение существует. при условии, что это отношение существует.
 , ,  . .
Если функция f(x) имеет производную в некоторой точке х = х 0, то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во- первых функция может иметь разрыв в точке х 0, а во- вторых, даже если функция непрерывна в точке х 0, она может быть в ней не дифференцируема.
Пример: f(x) = ï x ï - имеет в точке х = 0 и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.
Теорема (необходимое условие существования производной) Если функция f(x) имеет производную в точке х0, то она непрерывна в этой точке.
Понятно, что это условие не является достаточным.
Основные правила дифференцирования
1. Производная константы равна нулю, т.е. 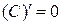 , где С - const. , где С - const.
2. Производная аргумента равна 1, т.е.  . .
3. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, т.е.

4. Производная произведения двух дифференцируемых функций:

Следствие. Постоянный множитель можно выносить за знак производной:  , где С - const. , где С - const.
5. Производная частного двух дифференцируемых функций:
 . .
при условии, что  . .
6. Производная сложной функции  , где , где  , где y и u – дифференцируемые функции своих аргументов, равна , где y и u – дифференцируемые функции своих аргументов, равна

Теорема. Для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной данной функции, т.е. 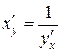 . .
Производные основных элементарных функций
Производная логарифмической функции:
 ; ;  . .
Производная показательной функции:
 ; ; 
Производная степенной функции:
 . .
Производные тригонометрических и обратных тригономнтрических функций:
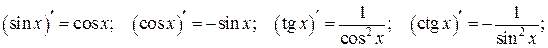

 Производная неявной функции Производная неявной функции  получается дифференцированием обеих частей уравнения, рассматривая y как функцию от x, а затем из полученного уравнения находится получается дифференцированием обеих частей уравнения, рассматривая y как функцию от x, а затем из полученного уравнения находится  : :
Примеры. Найти производные функций:
1) 
2) 

3) 
4)  . Преобразуем эту функцию, раскрывая скобки: . Преобразуем эту функцию, раскрывая скобки:  , ,  . .
5)  По формуле дифференцирования сложной функции имеем По формуле дифференцирования сложной функции имеем  , где , где 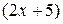 – производная аргумента – производная аргумента 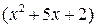 функции синус. функции синус.
6)  . Эта функция может быть представлена в виде . Эта функция может быть представлена в виде  . Отсюда . Отсюда 
7)  Эту функцию удобно преобразовать, пользуясь свойствами логарифмов: Эту функцию удобно преобразовать, пользуясь свойствами логарифмов:  . Тогда . Тогда 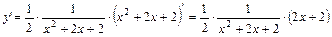 . .
8)  . .  . .
9)  . .
10.    . .
Производные высших порядков
Производная  называется производной 1-го порядка. Однако производная сама является функцией, которая также может иметь производную. называется производной 1-го порядка. Однако производная сама является функцией, которая также может иметь производную.
Производной n -го порядка называется производная от производной (n -1)-го порядка.
Обозначается:  и т.д. и т.д.
Механический смысл 2-й производной: 2-ая производная пути во времени  равна ускорению точки в момент равна ускорению точки в момент  . .
|