
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование функции и построение графика.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «МОСКОВСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ВЕТЕРИНАРНОЙ МЕДИЦИНЫ И БИОТЕХНОЛОГИИ ИМ. К.И. СКРЯБИНА» _______________________________________________________________
Джугели Т.П, Кишкинова О.А, Кутликова И.В, Федькина Т.В.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ФУНКЦИЯ ОДНОЙ ПЕРМЕННОЙ. ПРЕДЕЛ ФУНКЦИИ. ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА.
Москва 2011 УДК
Джугели, Т.П. Функция одной переменной. Предел функции. Исследование функции и построение графика: учеб.-метод. указ. / Т.П. Джугели,
В методических указаниях приведены необходимые теоретические сведения и формулы, даны решения типовых задач, приведены задания для расчетно-графической работы по разделу математики «Функция одной переменной. Предел функции. Исследование функции и построение графика».
Рекомендованы для студентов очной формы обучения по специальностям 111900.62 - «Ветсанэкспертиза», 111100 –«Зоотехния», 100800 – «Товароведение», 260200 – «Продукты питания животного происхождения», 260100 – «Продукты питания из растительного сырья», 020400 - «Биология»,
Рецензенты: профессор ФГБОУ ВПО МГАВМиБ им. К.И. Скрябина А.С. Белановский
Утверждены на заседании учебно-методической комиссии ветеринарно-биологического факультета ФГБОУ ВПО МГАВМиБ им. К.И. Скрябина
ВВЕДЕНИЕ Целью настоящих методических указаний по теме «Функция одной переменной. Предел функции. Исследование функции и построение графика» является познакомить студентов с теоретическим материалом, который необходим для подготовки высококвалифицированных специалистов в области сельского хозяйства и научной деятельности студентов в биологии и биотехнологии. В методических указаниях рассмотрены понятие функции, основные её свойства, понятие предела функции, непрерывности функции и приложения дифференциального исчисления к исследованию функции и построению её графика. Разобраны примеры нахождения предела функции, исследование функции и построение графиков, а также приведены варианты индивидуальной контрольной работы студентов и тестовые задания по данному разделу дисциплины. Одной из основных форм работы студента является самостоятельная работа над учебным материалом. Она состоит из непрерывной работы по изучению теоретического материала, по выполнению текущих заданий и контрольных работ. Результативность самостоятельной работы обеспечивается эффективной системой контроля, которая включает в себя опросы студентов по содержанию лекций, тестирование по отдельным разделам дисциплины, контрольные работы. При выполнении и оформлении домашней контрольной работы по теме «Исследование функции одной переменной» студент должен придерживаться следующих правил: а) в заголовке контрольной работы должны быть ясно выписаны фамилия студента, его инициалы, номер задания; б) контрольную работу следует выполнять в отдельной тетради, обязательно чернилами (не красными), с оставлением полей для замечаний преподавателя; в) решения контрольных задач следует располагать в порядке номеров, указанных в заданиях; перед решением каждой задачи надо выписывать полностью ее условие; г) графики функции должны быть выполнены на миллиметровой бумаге с указанием точек экстремума функции, точек перегиба, асимптот функции, единичных отрезков и осей координат. Контрольная работа, выполненная небрежно, без промежуточных вычислений, с пропуском задач и без соблюдения изложенных выше правил, возвращается обратно для переработки. Контрольная работа, выполненная не по своему варианту, не проверяется. Номер варианта соответствует номеру студента в списке группы.
I. ФУНКЦИЯ. СВОЙСТВА ФУНКЦИИ Понятие числовой функции Пусть задано числовое множество Х. Правило, сопоставляющее каждому числу х из множества Х единственное действительное число у, называют числовой функцией, заданной на множестве Х. х - независимая переменная (аргумент); у - зависимая переменная (функция). Символическая запись функции имеет вид у = f(х) Множество Х называется областью определения функции у и обозначается D(у). Е(у) - область (множество) значений функции у – множество всех значений переменной у, которые она принимает при всех допустимых значениях х. 1.2. Четность функции Функция у = f(х) называется четной, если для любого значения х, взятого из области определения функции, значение -х также принадлежит области определения и выполняется равенство f(х) = f(-х). Согласно определению, четная функция определена на множестве, симметричном относительно начала координат. График четной функции симметричен относительно оси ординат (рис. 1).
Рис. 1. График четной функции Примеры четных функций: Функция у = f(х) называется нечетной, если для любого значения х, взятого из области определения функции, значение -х также принадлежит области определения и выполняется равенство f(x)= -f(x). График нечетной функции симметричен относительно начала координат (рис. 2). Примеры нечетных функций:
Рис. 2. График нечетной функции
При построении графиков четных и нечетных функций достаточно построить только правую ветвь графика — для положительных значений аргумента. Левая ветвь достраивается симметрично относительно оси оy для четной функции и кососимметрично (т. е. симметрично относительно начала координат) для нечетной. Конечно, большинство функций не являются ни четными, ни нечетными. Таковы, например, функции: Периодичность Функция у=f(х) называется периодической с периодом Если Т – период функции, то при любом Наименьший положительный период функции называется её основным периодом. Сумма, разность, произведение и частное двух функций, имеющих период Т, обладает тем же периодом. Сумма n периодических функций с периодами Нули функции Нулем функции называется такое действительное значение х, при котором значение функции равно нулю. Для того чтобы найти нули функции, следует решить уравнение f(х)=0. Действительные корни этого уравнения являются нулями функции у=f(х),и обратно. Нули функции представляют собой абсциссы точек, в которых график этой функции либо пересекает ось абсцисс, либо касается ее. Например, функция у = х3- 3x имеет нули в точках х = 0, Функция может и не иметь нулей. Такова, например, функция Монотонность функции. Переменную величину называют монотонной, если она изменяется только в одном направлении, т.е. либо только возрастает, либо только убывает. Очевидно, что движение точки х в сторону положительного направления оси абсцисс является монотонно возрастающим, а в противоположную сторону - монотонно убывающим. Функция у = f(х) называется монотонно возрастающей на интервале (а, b), если для любых х1, и х2, принадлежащих этому интервалу, из неравенства х2 > х1, следует неравенство f (х 2 ) > f(x 1 ) (рис. 3а). Функция у = f(х) называется монотонно убывающей на интервале (а, b), если для любых х1 и х2, принадлежащих этому интервалу, из неравенства х2 > х1, следует неравенство f (x2 ) < f(x1) (рис. 3б).
Рис. 3. Графики монотонно возрастающей и монотонно убывающей функций.
Естественно, что интервал (а, b)предполагается взятым из области определения функции. Экстремумы функции Пусть функция у = f(х) определена на отрезке [а;b]. Говорят, что функция Под окрестностью точки х0 понимают интервал длины 2e с центром в точке х0, т.е. (х0-e, х0+e), где e - произвольное положительное число Говорят, что функция у = f(х) имеет локальный минимум в точке х0 є[а;b], если существует окрестность точки х0, целиком содержащаяся в [а;b] и такая, что для любого х, принадлежащего этой окрестности, выполняется неравенство f(х) > f(х0). Достаточный признак экстремума функции. Критическая точка (внутренняя точка области определения функции, в которой производная этой функции равна нулю или не существует) является точкой экстремума функции, если в окрестности этой точки производная меняет знак, причем точкой максимума, если производная меняет знак с «+» на «-», и точкой минимума, если производная меняет знак с «-» на «+». Наибольшее (наименьшее) значение непрерывной функции у = f(х) на отрезке [а;b] достигается либо в одной из критических точек, либо в одной из граничных точек данного отрезка. Выпуклость функции Говорят, что функция у = f(х) выпукла вверх в точке х0, если существует окрестность точки х0 такая, что для всех ее точек х касательная к графику функции в точке М0(х0, у0) лежит выше графика (рис. 4а). Говорят, что функция Если на некотором промежутке (а;b ) все касательные к графику функции
Рис. 4. Графики выпуклой функции Понятие предела функции Число А называется пределом функции в точке х0 (или при х Обозначают Теоремы о пределах 1. 2. 3. 4. 5. Первый замечательный предел Второй замечательный предел
Правило Лопиталя. Пусть функции
Односторонние пределы Бывают случаи, когда способ приближения аргумента х к х0 существенно влияет на значение предела функции. Поэтому вводят понятия односторонних пределов. Число А1 называется пределом функции y= f(x) слева в точке х0, если для любого числа Аналогично определяется предел функции справа. Число А2 называется пределом функции y= f(x) справа в точке х0, если для любого числа Пределы функции слева и справа называются односторонними пределами. Непрерывность функции Функция
А также говорят, функция
Существует теорема о непрерывности функции в точке. Функция y= f(x) непрерывна в точке x0, тогда и только тогда, когда функция имеет конечные пределы в точке x0 и предел функции в точке x0 равен значению функции в этой точке.
Все элементарные функции непрерывны в области своего определения. Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Для элементарных функций справедливы следующие положения: 1. область непрерывности элементарной функции совпадает с её областью определения, т.е. элементарная функция непрерывна во всей области определения 2. элементарная функция может иметь разрыв только в отдельных точках какого-либо промежутка, но не во всех его точках 3. элементарная функция может иметь разрыв только в той точке, в которой она не определена. Функция называется непрерывной в промежутке (замкнутом или открытом), если она непрерывна во всех точках этого промежутка. Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Точка разрыва х0 называется точкой разрыва первого рода функции При этом: если А1=А2, то точка х0 называется точкой устранимого разрыва (рис.6) если Величину
Рис. 6. График функции с устранимым разрывом
Рис. 7. График функции с конечным разрывом
Точка х0 называется точкой разрыва 2-го рода, если по крайней мере один из односторонних пределов не существует или равен ∞ (рис.8).
Рис. 8. График функции с точкой разрыва 2-го рода
Замена переменной Пример: Найти Решение: При непосредственной подстановке предельного значения x=1 числитель и знаменатель обращаются в нуль.
Имеем неопределённость вида Затем после преобразований сократим дробь на общий множитель.
Первый замечательный предел
Примеры: 1. Найти Решение: При
Имеем неопределённость вида
Ответ: 2. Найти Решение: При
Имеем неопределённость вида
Ответ: 3. Найти Решение: При
Имеем неопределённость вида
Ответ: Правило Лопиталя Найти Решение:
Ответ: 1 3.2. Неопределенность вида Замена переменной Пример: Найти Решение: Имеем неопределённость вида
3.4. Неопределенность вида IV. АСИМПТОТЫ КРИВОЙ
Прямая называется асимптотой кривой y=f(x), если расстояние от точки М(x;y) до этой прямой стремится к 0 при стремлении хотя бы одной из координат к ∞ Вертикальные асимптоты. График функции Горизонтальные асимптоты. График функции
Рис. 9. Графики функций, имеющие горизонтальные асимптоты
Наклонные асимптоты. Если существуют пределы
V. ПРИМЕРЫ ИССЛЕДОВАНИЯ ФУНКЦИЙ
Примеры: 1. 1) D(y)=R, E(y)=R (находим по графику) 2) Непрерывность. Асимптоты. Так как функция
Асимптот нет. 3) Четность. Так как область определения функции симметрична относительно нуля, выясним, имеют ли место следующие равенства:
Следовательно, функция является нечётной. Её график симметричен относительно начала координат. 4) Функция не является периодической. 5) Нули функции
или (0;0); 6) Монотонность функции. Экстремумы функции.
x=0,
max min 7) Выпуклость. Точки перегиба.
x=0 или
т. перегиба т. перегиба т. перегиба 8) График
2. 1) 2) Непрерывность. Асимптоты. Данная функция определена при всех значениях
Следовательно, функция Найдем наклонные асимптоты.
Итак, 3) Четность. Область определения не симметрична относительно нуля, поэтому функция не является ни четной, ни нечетной. 4) Функция не является периодической. 5) Нули функции. y=0, если x2-x=0; x(x-1)=0; x1=0 или x2=1 (0; 0), (1; 0) – точки пересечения графика с осями координат. 6) Монотонность. Точки экстремума.
2x2+2x-1=0 D=4+8=12
max min 7) Выпуклость. Точки перегиба.
Точек перегиба нет 8) График
3. 1) D(y)=R, E(y)= 2) Непрерывность. Асимптоты. Функция непрерывна на всей числовой прямой. Точек разрыва нет. Следовательно, вертикальных асимптот нет. Исследуем поведение функции на концах области определения.
При 3) Четность. Область определения не симметрична относительно нуля, поэтому функция не является ни четной, ни нечетной. 4) Функция не является периодической. 5) Нули функции. y=0, если x=-1 Если x=0, то
6) Монотонность. Экстремумы функции.
min 7) Выпуклость. Точки перегиба.
т. перегиба 8)
VI. ВОПРОСЫ И ЗАДАЧИ ДЛЯ САМОПРОВЕРКИ
1. Что такое функция? 2. Какая функция называется бесконечно малой, бесконечно большой? 3. Какова связь между бесконечно малой и бесконечно большой функциями? 4. Сформулируйте основные теоремы о пределах. 5. Дайте определение непрерывной функции в точке и на промежутке. 6. Сформулируйте необходимый и достаточный признаки убывания (возрастания) функции на интервале. 6. Что называется экстремумом функции на интервале? 7. Сформулируйте необходимое и достаточное условие существования экстремума. 8. Дайте определения выпуклости и вогнутости кривой на интервале. 9. Что называется точкой перегиба графика функции? Алгоритм нахождения точек перегиба. 10. Сформулируйте достаточный признак существования точки перегиба. 11. Изложите общую схему исследования функции и построения ее графика.
Найти пределы:
VII. ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ ПО ТЕМЕ: «ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ЕЕ ГРАФИКА»
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 538; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.249.76 (0.009 с.) |





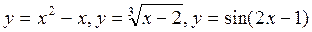
 , если при всех значениях х из области её определения выполняются равенства
, если при всех значениях х из области её определения выполняются равенства 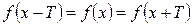 .
. \
\  число
число  также является периодом функции.
также является периодом функции. имеет период
имеет период  . Если функция у = f(х) имеет период Т, то функция
. Если функция у = f(х) имеет период Т, то функция  имеет период
имеет период  .
.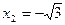 ,
,  , а функция
, а функция 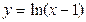 имеет нуль в точке х = 2.
имеет нуль в точке х = 2.


 х0), если для любого положительного числа
х0), если для любого положительного числа  найдется такое положительное число
найдется такое положительное число 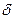 , что для всех х
, что для всех х  х0 , удовлетворяющих неравенству
х0 , удовлетворяющих неравенству 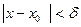 , выполняется неравенство
, выполняется неравенство 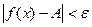 .
.


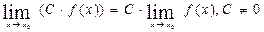






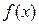 и
и  непрерывны и дифференцируемы в окрестности точки x0 и обращаются в нуль в этой точке:
непрерывны и дифференцируемы в окрестности точки x0 и обращаются в нуль в этой точке:  . Пусть
. Пусть  в окрестности точки x0. Если существует предел
в окрестности точки x0. Если существует предел  , то
, то  .
. существует число
существует число  такое, что при х
такое, что при х 
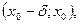 выполняется неравенство
выполняется неравенство  . Предел слева записывают так:
. Предел слева записывают так:  или коротко:
или коротко:  (обозначение Дирихле).
(обозначение Дирихле). выполняется неравенство
выполняется неравенство  . Предел справа записывают так:
. Предел справа записывают так:  . Коротко предел справа обозначают f(xo+0)=A2.
. Коротко предел справа обозначают f(xo+0)=A2. называется непрерывной в точке
называется непрерывной в точке  , если предел функции при
, если предел функции при  равен значению функции при
равен значению функции при  .
. называется непрерывной в точке
называется непрерывной в точке  .
.
 , если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е
, если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е  и
и 
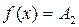 .
. , то точка х0 называется точкой конечного разрыва (рис.7).
, то точка х0 называется точкой конечного разрыва (рис.7). называют скачком функции
называют скачком функции





 . Для раскрытия неопределённости избавимся от иррациональности сделав замену
. Для раскрытия неопределённости избавимся от иррациональности сделав замену  (x=t3). Тогда при
(x=t3). Тогда при 
 .
. Ответ: 4
Ответ: 4
 числитель и знаменатель обращаются в нуль.
числитель и знаменатель обращаются в нуль.














 . Для раскрытия неопределённости сделаем замену x=−t (t=-x, t→+∞ при x→−∞), а затем разделим почленно числитель и знаменатель на наивысшую степень t, т.е. на t5.
. Для раскрытия неопределённости сделаем замену x=−t (t=-x, t→+∞ при x→−∞), а затем разделим почленно числитель и знаменатель на наивысшую степень t, т.е. на t5. Ответ:
Ответ: 

 или
или  ; при этом точка
; при этом точка  или при
или при 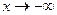 имеет горизонтальную асимптоту, если
имеет горизонтальную асимптоту, если  или
или 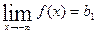 . Может оказаться, что либо только один из этих пределов конечный, либо ни одного. Тогда график имеет или одну горизонтальную асимптоту, или ни одной. Уравнение горизонтальной асимптоты имеет вид
. Может оказаться, что либо только один из этих пределов конечный, либо ни одного. Тогда график имеет или одну горизонтальную асимптоту, или ни одной. Уравнение горизонтальной асимптоты имеет вид  (рис. 9).
(рис. 9).
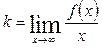 и
и  , то прямая y=kx+b является наклонной асимптотой кривой при указанном стремлении x. При x →
, то прямая y=kx+b является наклонной асимптотой кривой при указанном стремлении x. При x →  асимптоты могут быть различны.
асимптоты могут быть различны.



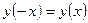 или
или  .
.



 - точки пересечения графика с осями.
- точки пересечения графика с осями.



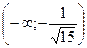















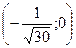

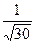



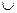


 , E(y)=
, E(y)=  (определяем в конце задания после построения графика функции).
(определяем в конце задания после построения графика функции). , кроме
, кроме  . Так как функция
. Так как функция 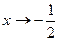 .
. .
. .
.

 и
и  . Следовательно, при
. Следовательно, при  .
.
 , если 2x2+2x-1=0
, если 2x2+2x-1=0



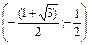















 (определяем в конце задания после построения графика функции).
(определяем в конце задания после построения графика функции).

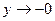 . Следовательно, при
. Следовательно, при 


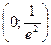 - точки пересечения с осями.
- точки пересечения с осями.






 , если x=-3
, если x=-3

















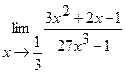







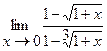




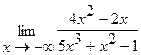


 2.
2. 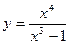 3.
3. 


