
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимый признак возрастания (убывания).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если дифференцируемая интервале Достаточный признак возрастания (убывания) функции. Если функция у =f(х) дифференцируема на интервале Экстремумы функции Пусть функция у = f(х) определена на отрезке [а;b]. Говорят, что функция Под окрестностью точки х0 понимают интервал длины 2e с центром в точке х0, т.е. (х0-e, х0+e), где e - произвольное положительное число Говорят, что функция у = f(х) имеет локальный минимум в точке х0 є[а;b], если существует окрестность точки х0, целиком содержащаяся в [а;b] и такая, что для любого х, принадлежащего этой окрестности, выполняется неравенство f(х) > f(х0). Достаточный признак экстремума функции. Критическая точка (внутренняя точка области определения функции, в которой производная этой функции равна нулю или не существует) является точкой экстремума функции, если в окрестности этой точки производная меняет знак, причем точкой максимума, если производная меняет знак с «+» на «-», и точкой минимума, если производная меняет знак с «-» на «+». Наибольшее (наименьшее) значение непрерывной функции у = f(х) на отрезке [а;b] достигается либо в одной из критических точек, либо в одной из граничных точек данного отрезка. Выпуклость функции Говорят, что функция у = f(х) выпукла вверх в точке х0, если существует окрестность точки х0 такая, что для всех ее точек х касательная к графику функции в точке М0(х0, у0) лежит выше графика (рис. 4а). Говорят, что функция Если на некотором промежутке (а;b ) все касательные к графику функции
Рис. 4. Графики выпуклой функции Отыскание интервалов выпуклости и точек перегиба Достаточное условие выпуклости функции на интервале. Если вторая производная f"(х) существует на интервале (а, b) и не меняет знак на этом интервале, то: 1) при f"(х) > 0 (знак +) функция f(х) выпукла вниз на интервале (а;b); 2) при f"(х) < 0 (знак -) функция f(х) выпукла вверх на интервале (а;b). Таким образом, для нахождения интервалов выпуклости вверх и выпуклости вниз функции нужно найти вторую производную и решить неравенства Точка М0 (х0; f(х0)) графика функции у = f(х) называется точкой перегиба этого графика, если существует такая окрестность точки х0, в пределах которой график функции у = f(х) слева и справа от т. М0 имеет разные направления выпуклости. На рис. 5 изображен график функции, имеющей перегиб в точке М0(х0; f (х0)).
Рис. 5. График функции, имеющей перегиб
Необходимый признак существования точки перегиба. Если функция в точке х0 имеет перегиб, то вторая производная в этой точке либо не существует, либо равна нулю. Точки, в которых вторая производная обращается в нуль или не существует, называют критическими точками II-го рода. В этих точках перегиб может быть, а может и не быть. Этот вопрос решается с помощью следующего признака. Достаточный признак существования точки перегиба. Пусть функция определена и непрерывна в некоторой окрестности точки х0, включая саму точку. Пусть, далее, вторая производная в этой точке равна нулю или не существует. Тогда, если f"(х) < 0 при х <х0 и f"(х) > 0 при х > х0 или f"(х) > 0 при х < х0 и f"(х) < 0 при х > х0, то М0(х0, (f(х0)) является точкой перегиба кривой у = f(х).
II. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ Понятие предела функции Число А называется пределом функции в точке х0 (или при х Обозначают
|
|||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1252; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.5.44 (0.01 с.) |

 функция f(х) возрастает (убывает), то
функция f(х) возрастает (убывает), то  (
( ) для всех
) для всех  .
. для всех
для всех  может быть равна 0 в отдельных точках промежутка
может быть равна 0 в отдельных точках промежутка 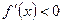 (или равна 0 в отдельных точках промежутка
(или равна 0 в отдельных точках промежутка  для всех
для всех 


 х0), если для любого положительного числа
х0), если для любого положительного числа  найдется такое положительное число
найдется такое положительное число 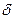 , что для всех х
, что для всех х  х0 , удовлетворяющих неравенству
х0 , удовлетворяющих неравенству 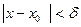 , выполняется неравенство
, выполняется неравенство 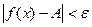 .
.



