
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
III. Методы раскрытия неопределенностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При решении заданий на вычисление предела функции одной переменной встречаются различные виды неопределенностей. А именно: неопределенность вида Различные виды неопределенностей имеют свои методы раскрытия. 3.1. Неопределенность вида Разложение числителя и знаменателя на множители с последующим сокращением Примеры: 1. Найти Решение: При непосредственной подстановке предельного значения x=1 числитель и знаменатель обращаются в нуль.
Имеем неопределённость вида Для квадратного трёхчлена Где Для 3x2+x-4 получим:
Для
Тогда
Ответ: -7 2. Найти Решение: При непосредственной подстановке предельного значения x=1 числитель и знаменатель обращаются в нуль.
Имеем неопределённость вида Для квадратного трёхчлена:
где Для
Числитель разложим на множители следующим образом: Тогда Ответ: 3. Найти Решение: При непосредственной подстановке предельного значения x=3 числитель и знаменатель обращаются в нуль
Имеем неопределённость вида Для квадратного трёхчлена
где Для
Знаменатель разложим по формуле
Для Тогда Ответ:
Деление многочлена на многочлен 1. Найти Решение:
2x²-2x 3x²-3 -(2x²-2x) -(3x²-3x)
0 3x-3 -(3x-3)
Разложим числитель и знаменатель на множители и сократим дробь:
Вычислим предел:
Ответ: Устранение иррациональных разностей домножением на сопряженное выражение Примеры: 1. Найти Решение: При непосредственной подстановке предельного значения x=0 числитель и знаменатель обращаются в нуль.
Имеем неопределённость вида А затем при наличии общего множителя сократим на него дробь.
2. Найти Решение: При непосредственной подстановке предельного значения x=1 числитель и знаменатель обращаются в нуль.
Имеем неопределённость вида
3. Найти Решение: При непосредственной подстановке предельного значения x=0 числитель и знаменатель обращаются в нуль.
Имеем неопределённость вида
Ответ: Замена переменной Пример: Найти Решение: При непосредственной подстановке предельного значения x=1 числитель и знаменатель обращаются в нуль.
Имеем неопределённость вида Затем после преобразований сократим дробь на общий множитель.
Первый замечательный предел
Примеры: 1. Найти Решение: При
Имеем неопределённость вида
Ответ: 2. Найти Решение: При
Имеем неопределённость вида
Ответ: 3. Найти Решение: При
Имеем неопределённость вида
Ответ: Правило Лопиталя Найти Решение:
Ответ: 1 3.2. Неопределенность вида
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.163.120 (0.006 с.) |

 ,
,  ,
,  ,
,  ,
,  .
.






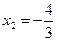


 получим:
получим: 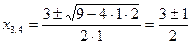








 получим:
получим: 









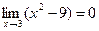
 получим:
получим: 


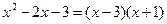

 получим:
получим: 




 =
=  -неопределенность, для раскрытия требуется дробь сократить.
-неопределенность, для раскрытия требуется дробь сократить. Так как x=1 – корень многочленов, то многочлены кратны одночлену (x – 1):
Так как x=1 – корень многочленов, то многочлены кратны одночлену (x – 1):
 -(x³-x²) x²+2x -(3x³-3x²) 3x²+3x+3
-(x³-x²) x²+2x -(3x³-3x²) 3x²+3x+3
 .
.


 для раскрытия неопределённости домножим числитель и знаменатель на сопряжённый двучлен
для раскрытия неопределённости домножим числитель и знаменатель на сопряжённый двучлен  ,
, Ответ:
Ответ: 


 и
и  , а затем при наличии общего множителя сократим на него дробь
, а затем при наличии общего множителя сократим на него дробь Ответ:
Ответ: 


 и
и 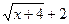 , а затем при наличии общего множителя сократим на него дробь.
, а затем при наличии общего множителя сократим на него дробь.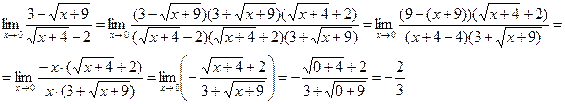




 (x=t3). Тогда при
(x=t3). Тогда при 
 .
. Ответ: 4
Ответ: 4

 числитель и знаменатель обращаются в нуль.
числитель и знаменатель обращаются в нуль.















