
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы исследования операцийСодержание книги
Поиск на нашем сайте
Под исследованием операций понимают совокупность принципов, методов и средств, позволяющих решать задачи выбора наилучших вариантов. Методология исследования операций оказалась эффективной при решении многих задач в различных областях техники [30], [33]. Выбор наилучшего варианта всегда связан с компромиссными решениями, которые принято называть оптимальными. При этом под оптимальным понимается решение, минимизирующее или максимизирующее некоторый критерий (целевую функцию), при заданной системе ограничений. Если оптимизация проводится по параметрам, то ее называют параметрической; если же оптимизируется последовательность технологических операций, состав оборудования, ее называют структурной. В методическом отношении исследование операций разделяется на этапы: разработка математической модели явления (операции); выбор критерия оценки качества; подготовка (систематизация) необходимой информации и исследование модели математическими методами. Отыскание оптимального решения называют математическим программированием. Охарактеризуем в краткой форме каждый из указанных этапов решения оптимизационных задач [5]. Модели функционирования технических объектов необходимы для нахождения оптимальных характеристик. Построение модели начинается с четкого уяснения и формулирования цели исследования. Далее необходимо выявить основные процессы, протекающие в объекте, и факторы, определяющие их протекание. С учетом указанного строится математическая модель, в которой получают отражение основные процессы и вызываемые ими изменения в исследуемом показателе. При этом возможны два подхода: Физический, когда в основе модели лежат закономерности физико-химических процессов (явлений), протекающих в объекте. Экспериментально-статистический, базирующийся на статистической обработке опытных данных. При параметрической оптимизации схема модели представляется в виде черного ящика (рис. 19). На входе управляемые переменные х, контролируемые, но не управляемые переменные г и случайные возмущения е. На выходе - оцениваемые переменные у (отклик).
Рис. 19. Представление объекта при параметрической оптимизации При этом оптимизация сводится к нахождению и реализации таких способов варьирования управляемыми процессами, при которых в рамках установленных ограничений обеспечивается получение экстремума (максимума или минимума) целевой функции, несмотря на изменение контролируемых переменных и влияние случайных возмущений. Критерий (целевая функция), будучи показателем операции, должен быть представительным (соответствующим цели исследования), чувствительным к исследуемым параметрам и по возможности простым. Желательно также, чтобы критерий был единственным; в случае необходимости оптимизации по нескольким параметрам из них обычно выбирают наиболее важный, а остальные переводят в ограничения. Общей формой критерия в этом случае будет математическое ожидание затрат (в различном выражении, например, через стоимость) при заданной эффективности (она выступает в виде ограничения), т.е.
Возможна и обратная постановка задачи. Оптимальным решением является такое, которое обеспечивает максимум эффективности при фиксированных затрат, т.е.
Соответственно этой общей форме критерии могут конкретизироваться с выражением затрат, например по массе, объему и т.п.; эффективность может выражаться также через количество произведенных изделий, полезное время работы и другие параметры. Могут быть и более частные ограничения, например по массе, габаритам, перегрузкам. В качестве характеристик исследуемых технических объектов используются производительность, надежность, стоимость, весовые параметры и габаритные размеры. Наибольшие практические трудности возникают при оценке стоимости, во-первых, потому, что ее определению до перехода к рыночной экономике не уделялось должного внимания и не накоплен в этом плане необходимые опыт и навыки, во-вторых, рыночные цены помимо производственных затрат и издержек определяются еще и конъюнктурой рынка (спросом). Вместе с тем это не является препятствием для рассмотрения (изучения) методологии оценки влияния стоимости при оптимизации, поскольку она не зависит от количественного выражения стоимости. В связи с этим при дальнейшем изложении будем оперировать ценами, имеющими условный характер. В целях облегчения формирования необходимой информации по стоимостям в будущем приведем некоторые практически важные рекомендации [33]. Существуют общие зависимости, связывающие стоимость С детали (узла) с точностью ее изготовления и надежностью
где А, В, h - коэффициенты; δ - допуск на изготовление;
где Для каждого типа технического устройства имея опытные данные с использованием методов аппроксимации можно получить зависимости вида
или
где ζi- - характеристика технического устройства; Напомним также, что стоимость эксплуатации исследуемого объекта применительно ко всем режимам определяется затратами на энергетику, текущий и капитальный ремонт, на содержание обслуживающего персонала. Математическое программирование - это план действия (программа) и методология решения оптимизационных задач. Главным вопросом здесь является выбор математического метода. Не существует одного метода, лучшего, чем все остальные, для решения всех типов задач [12]. Более того, одна и та же задача может быть решена разными методами. В связи с этим математическое программирование требует творческих усилий, умения учитывать специфику постановки задач. Задачи оптимизации по виду целевой функции и задаваемым ограничениям можно разделить на линейные и нелинейные [1]. Задачи линейного программирования обычно сводятся к распределению ограниченных ресурсов по нескольким взаимно связанным по цели и использованию ресурсов видам производственной деятельности. Соответствующие модели характеризуются линейными функциями с ограничениями. Напомним, что линейность означает наличие двух свойств - пропорциональности и аддитивности. В общем случае при решении задач линейного программирования требуется найти набор переменных, максимизирующих (минимизирующих) функцию вида
при ограничениях
В случае двух и трех переменных задача легко решается графически. Общим же методом решения таких задач является симплекс-метод. Симплексом называется k-мерный выпуклый многоугольник, имеющий Сущность симплекс-метода заключается в последовательном (упорядоченном) вычислении значений целевой функции, начиная с некоторой исходной допустимой точки до тех пор, пока не будет найдено оптимальное значение. При этом каждая последующая (угловая) точка должна быть смежной с предыдущей; переход осуществляется по границам (ребрам) многоугольника; процесс решения продолжается до получения оптимального плана [8]. Если все или некоторые переменные принимают целочисленные значения, то задача является целочисленной (полностью или частично). Решение целочисленных задач затрудняется появлением ошибок округления, что особенно важно при малых значениях переменных. Такие задачи решаются методом отсечения или комбинаторными методами. В первом случае путем введения дополнительных ограничений многогранник допустимых решений постепенно деформируется до тех пор, пока координаты оптимального решения не станут целочисленными. В основе второго метода лежит идея перебора всех допустимых целочисленных решений с разбиением пространства решений и отбрасыванием областей, не содержащих допустимых целочисленных решений. Задачи нелинейного программирования очень многообразны и отличаются большей сложностью; для них характерно наличие нелинейных функций [23]. Таким задачи могут быть без ограничений и с ограничениями в виде равенств и неравенств. Если модель характеризуется дифференцируемыми функциями без ограничений, решение основывается на отыскании корней уравнений: при одной переменной
при двух переменных
Если модель представлена сложными функциями - функционалами, в которых роль независимых переменных играют функции, применяют методы вариационного исчисления. Если модель представляется функциями, для которых вычисление производных методами анализа практически невозможно, следует переходить к численным методам. Самым простым и универсальным приемом отыскания экстремума при этом является полный перебор (пассивный поиск). Сущность этого приема заключается в вычислении значений функции при различных (всех) значениях аргумента с последующим сопоставлением результатов (метод сравнения). Такой перебор из-за большого объема вычислений приемлем лишь при сравнительно малом числе возможных вариантов; особенно он эффективен при дискретных значениях аргумента. Значительного сокращения объема вычислений можно достичь при применении направленного перебора. Особенно эффективным для функции с одной переменной является метод прямого поиска. При этом, прежде всего устанавливаются границы интервала, относительно которого точно известно, что он содержит точку экстремума. Затем этот интервал делится либо пополам, либо на какое-то другое число (с учетом ситуации на предыдущем шаге поиска). Теоретически длина оставшегося интервала может быть сделана сколь угодно малой. Надо, однако, иметь в виду, что отыскание экстремума гарантируется только применительно к унимодальной (одноэкстремальной) функции. Другим эффективным методом направленного перебора является градиентный метод, приемлемый для задач с дважды непрерывно дифференцируемыми целевыми функциями. Идея метода заключается в построении последовательности точек в направлении наискорейшего увеличения (уменьшения) значения функции. При этом поиск начинается с вычисления функции в точке, которая интуитивно представляется наиболее близкой к точке экстремума по соображениям общего характера (эвристическая точка). Затем берется вторая точка (шаг поиска Часто применяемым методом решения оптимизационных задач с ограничениями в виде равенств является метод Лагранжа. При этом исследуемую функцию представляют в виде функции Лагранжа
Условиями наличия экстремума в этом случае будут
Это означает, что задача оптимизации целевой функции Среди существующих методов решения оптимизационных задач особое место занимает динамическое программирование. Этот метод в известной мере универсален, с его помощью решаются многие из задач, как с нелинейными, так и линейными функциями. Динамическое программирование - это поэтапный метод оптимизации, приемлемый для решения задач, допускающих декомпозицию. При этом однократное решение сложной задачи заменяется многократным решением более простой; каждое последующее решение должно быть оптимальным относительно состояния в результате предыдущего решения (принцип оптимальности). Соответственно этому выстраивается и вычислительная процедура; задача решается в прямом или обратном направлении, причем в последнем случае, как правило, достигается более высокая эффективность. Решение задачи обычно начинается с построения сети (дерева), уяснения состояний с учетом связей между этапами, объема и характера необходимой информации. В общей постановке задачу динамического программирования и методологию ее решения можно сформулировать следующим образом. Из множества допустимых решений (управлений)
при Заметим, что функция достигаемого эффекта может быть как суммой, так и произведением, т. е.
или
где Наиболее типичными для динамического программирования являются задачи распределения, в которых какие-то ресурсы (капитальные вложения, масса, надежность и пр.) направляются на удовлетворение тех или иных потребностей (состояния - количество выделяемых ресурсов), замену изношенного и устаревшего оборудования (состояния - время работы объекта). Применение аналитических методов всегда предпочтительнее, так как при этом можно исследовать влияние разных факторов на искомое решение. Из численных методов наиболее общим и пригодным для решения задач оптимизации является динамическое программирование. В ряде случаев (при сравнительно малом числе вариантов) достаточно эффективен и самый простой метод полного перебора. Наконец, если задачу можно сформулировать в линейной постановке, то ее можно считать решенной. Если же приходится пользоваться методами поиска, предпочтение следует отдавать направленному поиску. Иногда возникает необходимость оптимизации при нескольких выходных параметрах, каждый из которых имеет свой физический смысл и свою размерность. В качестве обобщенного критерия при этом в принципе можно использовать функции желательности. При переходе к ним натуральные значения частных откликов преобразуются в безразмерные шкалы желательности; нижняя граница нуль - абсолютно неприемлемое значение; верхняя граница единица - наилучшее значение функции [22]. Построение шкалы желательности - это способ формализации представлений заинтересованных лиц о важности частных значений откликов, что естественно не лишено субъективности. При решении таких задач, во всяком случае, связанных с выбором материалов и упрочняющих технологий, представляется более целесообразным находить искомый компромисс сопоставлением значений (диаграмм) частных критериев по возможным вариантам с учетом мнений разработчиков и заказчиков (потребителей).
Лекция 12
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.76 (0.009 с.) |


 .
. при
при  .
.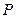 :
: , (17)
, (17)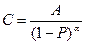 , (18)
, (18) и α – коэффициенты.
и α – коэффициенты. , (19)
, (19) , (20)
, (20) - коэффициенты.
- коэффициенты. (21)
(21)
 для
для 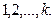
 вершин (симплекс нулевой размерности - точка, одномерный симплекс - отрезок прямой, двумерный - треугольник и т. д.).
вершин (симплекс нулевой размерности - точка, одномерный симплекс - отрезок прямой, двумерный - треугольник и т. д.).


 ) и находится приращение
) и находится приращение  ; в зависимости от знака приращения поиск продолжается вправе или влево с вычислением следующего значения
; в зависимости от знака приращения поиск продолжается вправе или влево с вычислением следующего значения  и т. д. до момента, когда приращение обращается в ноль (при непрерывном изменении аргумента будет остаточный интервал неопределенности L<
и т. д. до момента, когда приращение обращается в ноль (при непрерывном изменении аргумента будет остаточный интервал неопределенности L<  , где
, где  . (22)
. (22)

 при наличии ограничений g(xi) = 0 сводится к нахождению безусловного экстремума функции Лагранжа L(xi; λi). Методом множителей Лагранжа можно решать и задачи с ограничениями в виде неравенств, преобразуя их к виду равенств путем введения соответствующих дополнительных переменных.
при наличии ограничений g(xi) = 0 сводится к нахождению безусловного экстремума функции Лагранжа L(xi; λi). Методом множителей Лагранжа можно решать и задачи с ограничениями в виде неравенств, преобразуя их к виду равенств путем введения соответствующих дополнительных переменных. найти такие, которые приводят систему из начального состояния
найти такие, которые приводят систему из начального состояния  в конечное
в конечное  таким образом, что некоторый критерий Е достигает экстремального значения, т. е.
таким образом, что некоторый критерий Е достигает экстремального значения, т. е.

 (23)
(23) , (24)
, (24) - ресурс; Kj - варианты (переменные).
- ресурс; Kj - варианты (переменные).


