
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимизация выбора материалов,Содержание книги
Поиск на нашем сайте Технологий и оборудования
Применительно к оценке материалов - это заключительный этап выбора материала из предварительно подготовленного перечня марок, удовлетворяющих заданным требованиям, при соответствующей упрочняющей обработке. На этом этапе нередко приходится проводить испытания физических моделей или натуральных элементов (изделий), по результатам которых и принимается окончательное решение о выборе материала (опытная отработка). Однако проведение таких испытаний сопряжено с большими затратами и удлиняет сроки отработки изделия, особенно если ставится дополнительная задача оценки надежности по опытным данным. Решение оптимизационных задач в этом случае позволяет значительно уменьшить объем испытаний и сократить сроки их проведения. В общем случае под оптимизацией понимается комплекс мероприятий, направленных на достижение экстремального уровня некоторого обобщенного показателя качества. Под мероприятиями при этом понимаются математические приемы поиска экстремальных значений. Что касается обобщенных показателей, то из технических показателей такими являются характеристики надежности, а из нетехнических - экономическая эффективность, непосредственно связанная со стоимостью материала и технологическими затратами. В связи с этим, прежде чем рассматривать вопросы оптимизации выбора материалов, напомним некоторые положения из теории надежности [31] и исследования операций [30], необходимые для решения поставленной задачи.
Элементы теории надежности Технические изделия могут находиться либо в исправном, либо неисправном состояниях; в первом случае они соответствуют всем требованиям нормативно-технической документации, во втором - не соответствуют хотя бы одному из указанных требований. Исправные изделия всегда являются работоспособными и, следовательно, могут выполнять заданные функции, т.е. сохранять технические параметры в установленных пределах, обеспечивающих успешное использование по назначению. Неисправные же изделия будут работоспособными лишь тогда, когда они выполняют указанные выше функции. Неработоспособные изделия всегда являются неисправными. Событие, заключающееся в нарушении исправности изделия, называется повреждением (неисправностью), а в потере работоспособности - отказом. Надежность как техническое понятие связывается с работоспособностью изделий, с появлением отказов, с количественной оценкой наиболее важных аспектов качества технических изделий. Под надежностью понимается комплексное свойство изделия сохранять работоспособность в течение заданного времени или требуемой наработки. Надежность изделия в зависимости от назначения и условий эксплуатации может включить безотказность, долговечность, сохраняемость и ремонтопригодность (ГОСТ 27.002-89). С позиций выбора материалов наибольший интерес представляют первые три свойства. При этом под безотказностью понимается свойство изделия непрерывно сохранять работоспособность в течение установленного времени или заданной наработки. Долговечность же - свойство изделия непрерывно сохранять работоспособность до наступления предельного состояния при установленной системе технического обслуживания и ремонта. А сохраняемость - свойство изделия сохранять работоспособность (значения параметров в установлены пределах) в течение и после хранения и (или) транспортирования. Надежность изделия на всех стадиях разработки и этапах испытания проверяется (прогнозируется) применительно к условиям эксплуатации изделия и в этом смысле считается эксплуатационной (в дальнейшем - надежность). Количественно надежность оценивается с помощью показателей (критериев). Наиболее важным в плане решения задач выбора материалов является вероятность безотказной работы (безотказность), т.е. вероятность того, что в пределах установленного времени или заданной наработки отказ не возникает. В теории надежности разработаны методы ее проверки (определения и оценки) по результатам испытания применительно к имеющимся в наличии изделиям, а также прогнозирования в ходе разработки изделия [31]. Поскольку в данном случае надежность рассматривается с материаловедческих позиций, наибольший интерес представляют методы прогнозирования надежности, связанные с учетом свойств материалов, которые базируются на совокупности физических параметров, определяющих функционирование конструкции в условиях случайных возмущений при исключении внезапных отказов; применительно к материалу это обеспечивается определенным уровнем пластичности и вязкости, гарантирующим отсутствие хрупкого разрушения. Соответствующие методы основываются на математическом моделировании функционирования оцениваемых объектов (деталей) в предполагаемых условиях эксплуатации. Такая оценка производится путем сопоставления несущей способности детали (разрушающие нагрузки) с действующими эксплуатационными нагрузками. При этом нагрузка оценивается в широком смысле слова; под ней можно понимать не только механические, но и любые другие виды воздействия, например тепловые, электрические. Соответственно этому должна оцениваться и несущая способность; при механических воздействиях она будет отражать сопротивление разрушению или деформации. При таком подходе изделие будет работоспособным, если эксплуатационная нагрузка не будет превосходить несущей способности, соответствующей разрушающей нагрузке или ее предельно допустимому значению. Следовательно, применительно к одному условию оценки работоспособности, безотказность изделия будет
где Поскольку несущая способность вследствие неоднородности материалов носит случайный характер, как в большинстве случаев и эксплуатационная нагрузка, безотказность можно записать
или
В случае же нескольких условий работоспособности выражение (4) трансформируется:
где Несущая способность и действующие нагрузки при этом могут быть выражены и как функции случайных величин, которыми характеризуются, например, свойства материалов в процессе эксплуатации изделий. При решении практических задач соответствующие аналитические расчеты (моделирование) проводятся с помощью ранее указывавшихся и использовавшихся при решении статистических задач таблиц. Наиболее просто это делается при нормальном распределении нагрузок. Вот почему на практике обычно стремятся обрабатываемые данные привести к нормальному распределению. В связи с этим иногда представляется целесообразным вместо зависимости (2) для расчета безотказности пользоваться другими функциями работоспособности:
В случае нормального распределения вероятность безотказной работы при одном условии работоспособности по разности (2) определяется
Эту же величину можно выразить и через коэффициент запаса прочности:
В простейшем случае, когда разрушающая и действующая нагрузки не коррелированны Аналогичные зависимости применительно к другим условия работоспособности можно получить, определив средние квадратические отклонения функций работоспособности методом линеаризации; при некоррелированности нагрузок они соответственно зависимостям (6- 8) будут:
При этом принимается, что функция работоспособности мало отличается от линейной в области практически возможных значений действующих и разрушающих факторов. В случае необходимости полученные зависимости можно уточнить, основываясь на сохранении в разложении функций, кроме линейных составляющих, также членов более высокого порядка. Пример. Определить безотказность трубы толщиной 6,5 мм и диаметром 600 мм, изготовленной из стеклопластика типа ВФТС и нагруженной внутренним давлением, распределенным по нормальному закону со средним значением 4,19 МПа и средним квардатическим отклонением 1,25 МПа. Распределение оказалось нормальным, среднее значение предела прочности 372,7 МПа, а среднее квадратическое отклонение 40,2 МПа. Несущая способность трубы будет: среднее значение:
среднее квадратическое отклонение:
В соответствии с зависимостью (9), принимая во внимание независимость разрушающей и действующей нагрузок, определяем вероятность безотказной работы
Из таблиц Р= 0,995. Предположим, что для изделия установлен срок службы 5 лет. Прочность стеклотесктолита при этом понижается в соответствии с зависимостью до 331,6 МПа. Расчет, аналогичный предыдущему, дает снижение безотказности до Несколько сложнее задача решается в случае двух условий работоспособности одновременно. При нормальных распределениях нагрузок вероятность безотказности, как уже указывалось, определяется с помощью табличных функций по зависимостям: при
при
где
Необходимые для расчёта параметры при этом определяются:
Коэффициент корреляции рассчитывается по зависимости:
При независимости функций работоспособности показатель безотказности определяется: при последовательном соединении элементов
при параллельном соединении элементов
а при одинаковых (по надежности) элементах
где Пример. Определить надежность оболочки летательного аппарата, подвергающейся изгибающему моменту (поперечные перегрузки) и воздействию осевых сил (деформационная устойчивость), при исходных данных, представленных в табл. 3. В рассматриваемом случае нагрузки, обусловливающие предельное состояние оболочки, действуют в разные моменты времени и поэтому являются независимыми; соответствующие же несущие способности будут зависимыми, поскольку связаны с толщиной стенки. Они определяются: - разрушающим моментом
- разрушающей нагрузкой
где Условия работоспособности можно записать:
Таблица 3. Характеристика конструкции и материала оболочки
Определяем средние значения:
Находим средние квадратические отклонения
Корреляционный момент в соответствии с выражением (14) после преобразования с учётом вышеуказанных зависимостей будет:
а коэффициент корреляции
Далее определяем необходимые входные данные для вычисления надежности:
С помощью таблиц из работы [4] находим:
И наконец, в соответствии с выражением (12) рассчитываем:
В предположении независимости
Различие, как и следовало ожидать, незначительное, поскольку корреляция слабая, о чем свидетельствует сравнительно низкий коэффициент корреляции.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 432; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.85.59 (0.012 с.) |

 или (1)
или (1) , (2)
, (2) - несущая способность (разрушающая нагрузка или предельно допустимое значение нагрузки);
- несущая способность (разрушающая нагрузка или предельно допустимое значение нагрузки);  - эксплуатационная (действующая) нагрузка;
- эксплуатационная (действующая) нагрузка; 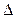 - функция работоспособности;
- функция работоспособности;  - условие работоспособности.
- условие работоспособности. (3)
(3) . (4)
. (4) , (5)
, (5) и
и 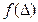 - плотность распределения несущей способности, действующей нагрузки и функции работоспособности соответственно.
- плотность распределения несущей способности, действующей нагрузки и функции работоспособности соответственно.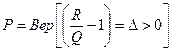 ; (6)
; (6) ; (7)
; (7) ; (8)
; (8) . (9)
. (9) , (10)
, (10) где
где  - значения соответствующих нагрузок;
- значения соответствующих нагрузок;  - их
- их  средние значения;
средние значения; 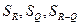 - средние квадратические отклонения;
- средние квадратические отклонения;  - коэффициент корреляции
- коэффициент корреляции  и
и  - коэффициенты вариации; - коэффициент запаса прочности (условный, по средним значениям);
- коэффициенты вариации; - коэффициент запаса прочности (условный, по средним значениям);  - параметр надежности (вероятности);
- параметр надежности (вероятности);  - нормированная функция нормального распределения.
- нормированная функция нормального распределения. , в формулах (9) и (10) последний член подкоренного выражения опускается.
, в формулах (9) и (10) последний член подкоренного выражения опускается. ; (11)
; (11) ; (11´)
; (11´) . (11´´)
. (11´´) ;
; .
. .
. . Аналогичным образом можно учесть изменение прочности материала при нагреве трубы, например, в рабочем режиме.
. Аналогичным образом можно учесть изменение прочности материала при нагреве трубы, например, в рабочем режиме. и
и  или
или  и
и  :
: (12)
(12) или
или  (13)
(13) и
и  - табулированные функции (см. табл. В и А в работе [4]); для последней справедливо соотношение:
- табулированные функции (см. табл. В и А в работе [4]); для последней справедливо соотношение: .
. ;
; ;
; ;
;
 . (14)
. (14) ; (15)
; (15) , (16)
, (16) , (16´)
, (16´) - показатель безотказности элементов, соответствующих условий работоспособности;
- показатель безотказности элементов, соответствующих условий работоспособности;  - число элементов.
- число элементов. ;
; ,
, – опытный коэффициент, зависящий от соотношения длины, радиуса и толщины оболочки (в данном случае
– опытный коэффициент, зависящий от соотношения длины, радиуса и толщины оболочки (в данном случае  ;
; .
.







 ;
; ;
;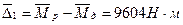 ;
; .
. ;
; .
. ,
, .
.

 ;
; 
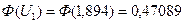 ;
; ;
;


 и
и  безотказность в соответствии с формулой (15) будет
безотказность в соответствии с формулой (15) будет



