
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы (основы) теории расписанийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Качество функционирования современного производства во многом определяется решениями, принимаемыми на этапах календарного планирования и оперативного управления. Особенно это актуально в связи с созданием современных автоматизированных производств – гибких производственных систем (ГПС). Системы оперативно – календарного планирования современных производств строятся в том числе и на достижениях так называемой «теории расписаний» [29]. Теория расписаний – это наука, занимающаяся исследованиями детерминированных обслуживающих систем на предмет оптимизации расписаний их функционирования. Примеры таких систем: · цех, участок, на станках которых осуществляется обработка деталей; · ВУЗ, где преподаватели обучают студентов и т.д. В любом случае имеется конечное множество требований (деталей, преподавателей и т.д.) Предполагается, что i – е требование на каждой стадии его обслуживания q (например, на каждой операции технологического процесса) может быть обслужено любым из приборов В теории расписаний рассматриваются различные системы обслуживания: · системы поточного типа, в которых каждое требование · системы с различными порядками (маршрутами) прохождения приборов требованиями и т.д. В частности, в последних системах с последовательными приборами для каждого требования В любом случае, если требование i на стадии q должно или может быть обслужено прибором Наряду с величинами Процесс функционирования обслуживающей системы может быть описан путем задания расписания (календарного плана, временного графика и т.п.). Расписание – некоторая совокупность указаний относительно того, какие именно требования какими именно приборами обслуживаются в каждый момент времени. Расписание рассматривается как совокупность Если При задании расписания должны соблюдаться все условия и ограничение, вытекающие из постановки рассматриваемой задачи, т.е. расписание должно быть допустимым [32]. Пример. На рис. 28 приведен график расписания
Рис. 28. График расписания обслуживания требований N = {1, 2, 3, 4} приборами M = {1, 2, 3} Здесь Прибор 1 во временном интервале Если существует несколько допустимых расписаний, то естественно необходимо выбрать лучшее из них. В теории расписаний качество расписания во многих случаях оценивают следующим образом. Каждое (допустимое) расписание S однозначно определяет вектор В частности, при построении оптимального по быстродействию расписания При построении расписания с наименьшим суммарным временем обслуживания При построении расписания с наименьшим временем смещения моментов завершения обслуживания требований i относительно сроков Оптимальное расписание может быть найдено в результате перебора конечного множества возможных вариантов. Основная трудность при этом состоит в том, что число таких вариантов очень велико и растет, по меньшей мере, экспоненциально с ростом размерности задачи. Известны так называемые эвристические алгоритмы формирования расписаний, алгоритмы на основе методов линейного и динамического программирования. Задачи составления расписаний для некоторых сложных систем обслуживания до сих пор не решены (NP – трудные задачи).
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 685; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.54.190 (0.006 с.) |

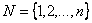 и конечное множество приборов (станков, групп студентов и т.д.)
и конечное множество приборов (станков, групп студентов и т.д.) 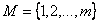 .
.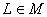 (но не более, чем одним одновременно). Предполагается также, что каждый прибор одновременно может обслуживать не более одного требования.
(но не более, чем одним одновременно). Предполагается также, что каждый прибор одновременно может обслуживать не более одного требования.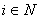 сначала обслуживается приборами первой группы, затем второй группы и т.д. пока не будет обслужено приборами последней r – ой группы;
сначала обслуживается приборами первой группы, затем второй группы и т.д. пока не будет обслужено приборами последней r – ой группы;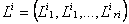 его обслуживания приборами. Требование i сначала обслуживается прибором
его обслуживания приборами. Требование i сначала обслуживается прибором 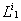 , затем
, затем 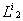 и т.д. пока не будет обслужено прибором
и т.д. пока не будет обслужено прибором 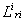 . Последовательности обслуживания могут быть различными для разных требований и могут содержать повторение приборов [32].
. Последовательности обслуживания могут быть различными для разных требований и могут содержать повторение приборов [32].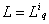 , то предполагается заданной длительность
, то предполагается заданной длительность 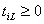 его обслуживания прибором. Запись
его обслуживания прибором. Запись  , как привило, означает, что по условию задачи требование i на стадии q прибором L не обслуживается.
, как привило, означает, что по условию задачи требование i на стадии q прибором L не обслуживается.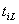 могут быть заданы также: момент
могут быть заданы также: момент 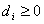 поступления требования i в систему; директивный срок
поступления требования i в систему; директивный срок 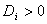 , к которому необходимо завершить обслуживание требования.
, к которому необходимо завершить обслуживание требования.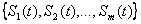 кусочно–постоянных непрерывных слева функций, каждая из которых задана на интервале
кусочно–постоянных непрерывных слева функций, каждая из которых задана на интервале 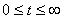 и принимает значения 0, 1, …, n.
и принимает значения 0, 1, …, n.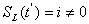 (здесь i – номер требования), то в момент времени
(здесь i – номер требования), то в момент времени 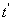 прибор
прибор 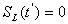 , то в момент времени
, то в момент времени 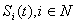 обслуживания требований
обслуживания требований 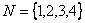 приборами
приборами  при различных маршрутах обслуживания требований. Все длительности обслуживания равны «1».
при различных маршрутах обслуживания требований. Все длительности обслуживания равны «1».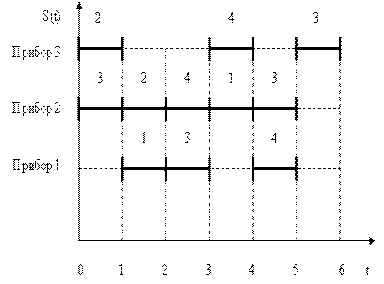
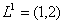 , т.е. первое требование обслуживается первым и вторым приборами,
, т.е. первое требование обслуживается первым и вторым приборами, 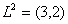 – второе требование обслуживается третьим и вторым приборами,
– второе требование обслуживается третьим и вторым приборами, 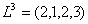 – третье требование обслуживается вторым, первым, снова вторым и третьим приборами,
– третье требование обслуживается вторым, первым, снова вторым и третьим приборами, 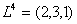 - четвертое требование обслуживается вторым, третьим и первым приборами.
- четвертое требование обслуживается вторым, третьим и первым приборами. 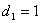 – момент поступления требования 1 в систему,
– момент поступления требования 1 в систему, 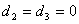 – моменты поступления требований 2 и 3 в систему,
– моменты поступления требований 2 и 3 в систему, 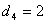 – момент поступления требования 4 в систему.
– момент поступления требования 4 в систему. 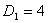 – директивный срок завершения обслуживания требования 1,
– директивный срок завершения обслуживания требования 1, 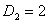 – директивный срок завершения обслуживания требования 2,
– директивный срок завершения обслуживания требования 2, 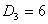 – директивный срок завершения обслуживания требования 3,
– директивный срок завершения обслуживания требования 3, 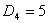 – директивный срок завершения обслуживания требования 4.
– директивный срок завершения обслуживания требования 4.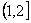 обслуживает требование 1, в интервале
обслуживает требование 1, в интервале 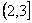 - требование 3, в интервале
- требование 3, в интервале 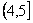 - требование 4. Прибор 2 в интервале
- требование 4. Прибор 2 в интервале 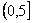 без простоев обслуживает требования 3, 2, 4, 1, 3 и т.д. Это расписание допустимо, т.е. каждый прибор одновременно обслуживает не более одного требования и i – е требование обслуживается одновременно не более, чем одним прибором.
без простоев обслуживает требования 3, 2, 4, 1, 3 и т.д. Это расписание допустимо, т.е. каждый прибор одновременно обслуживает не более одного требования и i – е требование обслуживается одновременно не более, чем одним прибором.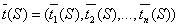 моментов завершения обслуживания требований. Задается некоторая действительная неубывающая по каждой из переменных функция
моментов завершения обслуживания требований. Задается некоторая действительная неубывающая по каждой из переменных функция 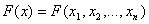 . Качество расписания S оценивается значением этой функции при
. Качество расписания S оценивается значением этой функции при 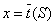 . Из двух расписаний лучшим считается то, которому соответствует меньшее значение
. Из двух расписаний лучшим считается то, которому соответствует меньшее значение 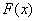 . Расписание, которому соответствует наименьшее значение
. Расписание, которому соответствует наименьшее значение 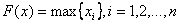 . В этом случае
. В этом случае 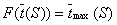 , где
, где 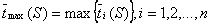 .
.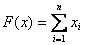 , при этом
, при этом 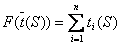 .
.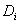 функция
функция 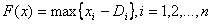 . При этом
. При этом 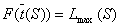 , где
, где 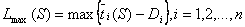 .
.


