
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производительность и надежность сблокированных автоматических линийСодержание книги
Поиск на нашем сайте
Математические модели, описывающие производительность и надежность автоматических линий (АЛ), рассмотрим на примере математических моделей сблокированных АЛ. В сблокированных АЛ все элементы соединены последовательно в смысле надежности, и отказ любого элемента приводит к отказу всей системы [19]. Прежде, чем разрабатывать математические модели АЛ, нужно выяснить, по какому закону распределены потоки отказов и потоки восстановлений (см. лекции по «теории массового обслуживания») механизмов и инструментов линии, т.к. это будет определять, какие теоретические положения будут заложены в основу модели. Впервые изучение вероятностных характеристик АЛ было начато в ЭНИМСе. При этом исходили из предположения, что потоки отказов и потоки восстановлений являются пуассоновскими, а периоды времени безотказной работы Позднее были проведены исследования этих потоков. Причем, в отличие от ранее выполненных работ потоки отказов и восстановлений оборудования и инструментов исследовали отдельно, т.к. природа этих потоков различна. Были получены следующие основные результаты. Среднестатистически для всех исследованных объектов экспоненциальный закон достаточно точно характеризует распределение случайных периодов восстановления оборудования. А для отдельных станков и инструментов экспериментальные законы распределения времени На этом рисунке: Для точной оценки функционирования конкретных станков и линий следует использовать математические модели с применением тех законов распределения, которые будут соответствовать реальным условиям эксплуатации оборудования. Мы рассмотрим первый вид математических моделей для простейших (пуассоновских) потоков, тем более, что нам известны соответствующие положения теории массового обслуживания, построенные на основе Марковских процессов [15].
Рис.17. Кривые распределения времени безотказной работы оборудования АЛ
Пусть сблокированная станочная система состоит из m – узлов и n – инструментов. Т.к. при такой компоновке все ее элементы соединены последовательно в смысле надежности и отказ любого элемента приводит к отказу всей системы, то вероятность отказа линии определится
где
Рис.18. Граф состояний сблокированной АЛ
На этом рисунке приняты следующие обозначения: S 0 - все элементы работоспособны; S 1 - отказ по вине инструментов; S 2 - отказ по вине механизмов (оборудования); В соответствие с положениями теории массового обслуживания вероятность того, что АЛ находится в состоянии
Вероятность пребывания линии в исправном состоянии характеризуется коэффициентом готовности -
Следует иметь в виду, что коэффициент готовности не равен коэффициенту технического использования АЛ. Коэффициент технического использования по сравнению с коэффициентом готовности дополнительно учитывает плановые простои (ремонты) АЛ. Если известны интенсивности
Для расчета коэффициента готовности АЛ Это дает возможность при проектировании АЛ выбирать такие технические средства (механизмы) и инструменты, которые обеспечат требуемый уровень надежности линии ( Таблица 1
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.10.139 (0.009 с.) |

 и восстановления
и восстановления  АЛ распределены по экспоненциальному закону. Вспомним, что для простейшего (пуассоновского) потока с интенсивностью
АЛ распределены по экспоненциальному закону. Вспомним, что для простейшего (пуассоновского) потока с интенсивностью 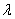 интервал
интервал  между соседними событиями имеет показательное (экспоненциальное) распределение с плотностью
между соседними событиями имеет показательное (экспоненциальное) распределение с плотностью  , где
, где  (ремонта),
(ремонта),  (смены инструментов) отличаются от теоретического экспоненциального – рис. 17.
(смены инструментов) отличаются от теоретического экспоненциального – рис. 17. - частота; X - относительные единицы; 1 – теоретическая кривая; 2 – экспериментальные кривые; 3 – среднестатистическая кривая. Расхождение между кривыми (1) и (3) – 7 – 10 %, а для отдельных станков расхождение между экспериментальными и теоретическими кривыми еще более значительное. Поэтому, показательный закон применяют в математических моделях, используемых для первоначальной оценки надежности станочных систем на ранней стадии их проектирования, когда не известны еще конструкции узлов и инструментов.
- частота; X - относительные единицы; 1 – теоретическая кривая; 2 – экспериментальные кривые; 3 – среднестатистическая кривая. Расхождение между кривыми (1) и (3) – 7 – 10 %, а для отдельных станков расхождение между экспериментальными и теоретическими кривыми еще более значительное. Поэтому, показательный закон применяют в математических моделях, используемых для первоначальной оценки надежности станочных систем на ранней стадии их проектирования, когда не известны еще конструкции узлов и инструментов.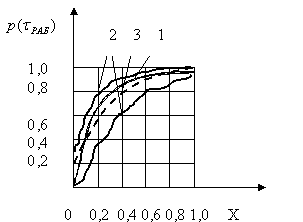
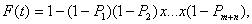
 - вероятность того, что 1, 2, …, (m + n) – й элемент АЛ находится в работоспособном состоянии. Выделим три состояния сблокированной системы (АЛ) – рис.18.
- вероятность того, что 1, 2, …, (m + n) – й элемент АЛ находится в работоспособном состоянии. Выделим три состояния сблокированной системы (АЛ) – рис.18.
 – интенсивности потоков отказов инструментов и оборудования;
– интенсивности потоков отказов инструментов и оборудования;  - интенсивности потоков восстановлений инструментов и оборудования.
- интенсивности потоков восстановлений инструментов и оборудования. определится:
определится:


 . Отношение
. Отношение  - это удельная длительность настройки элемента или группы элементов. Таким образом
- это удельная длительность настройки элемента или группы элементов. Таким образом


 для каждого инструмента и узла, то
для каждого инструмента и узла, то

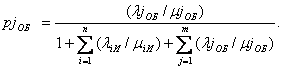
 путем длительных статистических исследований в производственных условиях были получены значения
путем длительных статистических исследований в производственных условиях были получены значения  и
и  для различных элементов АЛ. Примеры их значений приведены в таблице 1.
для различных элементов АЛ. Примеры их значений приведены в таблице 1. ) и цикловую производительность, можно рассчитать потенциальную производительность (
) и цикловую производительность, можно рассчитать потенциальную производительность ( ) и далее фактическую производительность
) и далее фактическую производительность  .
.



