
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитическая обработка экспериментальных данных методом наименьших квадратовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для понимания сути данного метода рассмотрим сначала рис. 5. На нем в обычных и логарифмических координатах изображены опытные значения (точки) и, соответственно, аппроксимирующая кривая и аппроксимирующая прямая.
Рис.5. Иллюстрация реализации метода наименьших квадратов
На данном рисунке y 1, y 2, …, y n – экспериментальные значения, f (x 1), f (x 2), …, f (x n) – расчетные значения аппроксимирующей функции. Аналогичные значения, но только в логарифмическом измерении, приведены на правой части рисунка. В основе метода наименьших квадратов лежит следующее положение: наилучшее приближение аппроксимирующей функции y = f (x) к экспериментальным данным будет в том случае, когда сумма квадратов отклонений расчетных значений f (x 1), f (x 2), …, f (x n) от экспериментальных данных y 1, y 2 … y n, является минимальной, т.е.
или
Разность Сумма S’ будет минимальной, если ее частные производные по параметрам C и k равны нулю. Произведя дифференцирование и соответствующие преобразования, получают систему нормальных уравнений, которая затем решается для нахождения искомой постоянной C и показателя степени k. Существуют компьютерные программы для обработки экспериментальных данных с целью получения аппроксимирующих функций, реализующие метод наименьших квадратов. Выражение После получения частных зависимостей их объединяют в общую зависимость. Пример объединения двух частных зависимостей. Пусть в результате проведения двух серий экспериментов получены следующие зависимости:
Обе серии экспериментов проводились при неизменных обрабатываемом и инструментальном материалах, скорости резания, СОТС и т.д [10]. Кроме этого первая серия экспериментов была выполнена при постоянной подаче s = s const, а вторая при постоянной глубине резания t = t const. Общая формула, выражающая одновременно влияние t и s на силу PZ, имеет вид:
Здесь неизвестна постоянная
Используя данные первой и второй серии опытов, получим:
Вследствие неизбежных погрешностей экспериментов величины
Подобным же образом объединяют три и более частных зависимости. Полученные формулы не являются физическими законами. Они получены на основе обработки вполне реальных экспериментальных данных, поэтому имеют определенную область адекватности. Т.е. за пределами этой области их использовать нельзя. Например, если силовая зависимость была получена для подач от 0,1мм/об до 0,5 мм/об, то при подачах меньше 0,1 или больше 0,5 мм/об эту формулу использовать нельзя. Всякая экстраполяция за пределами области адекватности может привести к существенным ошибкам в расчетах. Лекция 4-5 Математическое моделирование упругих деформаций в Технологической системе
При обработке деталей на металлорежущих станках сам станок, приспособление, инструмент и элементы его крепления, обрабатываемая заготовка представляют собой упругую систему, которая называется упругой системой СПИД. При обработке сила резания изменяется под действием переменных условий обработки, а именно неравномерности глубины резания, колебания твердости обрабатываемого материала и т.д. Колебания силы резания приводят к упругим деформациям деталей системы СПИД и смещению этих деталей по отношению друг к другу за счет наличия зазоров в соединениях. Кроме этого упругая система СПИД обладает не бесконечной жесткостью, причем эта жесткость также является случайной величиной, т.е. может изменять свое значение от наименьшего до наибольшего. Все это вместе взятое оказывает влияние на формирование точности обработки. Формирование упругих перемещений и смещения элементов в технологической системе и влияния их на точность обработки могут быть представлены следующей схемой – см. рис. 6.
Рис.6. Схема формирования упругих перемещений и смещения элементов в технологической системе и влияния их на точность обработки Жесткость упругой системы СПИД – это отношение составляющей силы резания, направленной по нормали к обрабатываемой поверхности, к смещению лезвия инструмента, установленного на размер в данном направлении. Таким образом, жесткость системы
где
Аналогично выражается жесткость отдельных элементов технологической системы: для суппорта – j суп, для передней бабки – j ПБ и т.д. Жесткость может быть выражена также отношением приращения силы резания
В практических расчетах иногда используют величину, обратную жесткости – податливость
Величина деформации упругой системы равна:
Для определения статической жесткости узла станка производят ряд нагружений, возрастающих от нуля до некоторого предельного значения, которое определяется размерами станка. Для каждого значения нагрузки измеряют смещение узла в направлении действия силы. Затем производят разгружение этого узла, постепенно уменьшая нагрузку и фиксируя остаточные
Рис. 7. Зависимости y = f(Py) при определении статической жесткости узла станка
отжатия. При нагружении и разгружении строятся зависимости При этом нагрузочная и разгрузочная ветви характеристики жесткости обычно не совпадают, т.е. имеет место гистерезис. Площадь петли гистерезиса – работа, затраченная на преодоление сил трения, контактных деформаций и т.д. При повторных циклах нагрузки площадь петли гистерезиса уменьшается вследствие выборки зазоров в стыках деталей при первом нагружении и уменьшения пластического деформирования. Для оценки жесткости в любой точке (например, в точке А) кривой
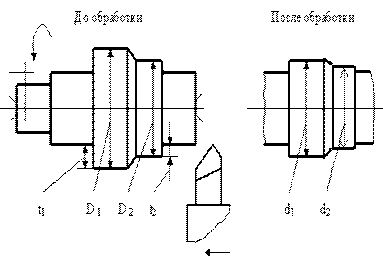
Численно производная равна тангенсу угла наклона касательной к кривой в точке А. Жесткость станка зависит от его конструкции и от качества сборки. Для многих станков жесткость и податливость регламентированы ГОСТами. Как показывает практика, статическая жесткость станков в 1,2 – 1,4 раза выше, чем жесткость работающих станков. Поэтому более объективной величиной является динамическая жесткость станков, которая определяется с помощью произвольного метода, который основан на обработке заготовок с переменным припуском и последующих расчетах [25]. Пример. Определение динамической жесткости токарного станка (рис.8). Пояски диаметрами D 1 и D 2 обрабатываются за один рабочий ход при неизменных условиях (подаче, скорости резания и т.д.). Уступ
Рис. 8. Схема испытания токарного станка для определения его динамической жесткости
Отношение
где Жесткость станка зависит и от степени его нагрева. Так, например, по наблюдениям профессора А.В.Худобина жесткость шпиндельной бабки круглошлифовального неработающего станка составляет 15100 Н/мм. После 30 мин его работы на холостом ходу жесткость достигла 22400 Н/мм, т.е. увеличилась на 44%. Жесткость узлов станков с вращающимися деталями не одинакова в радиальном направлении. Например, по данным Г. Б. Фикс – Марголина для токарных станков характерны следующие круглограммы жесткости шпиндельной группы (j) и упругих перемещений шпинделей (y), подобные приведенным на рис.9.
Рис.9. Круглограммы жесткости шпиндельной группы (j) и упругих перемещений шпинделей (y) токарных станков
Учитывая, что жесткость технологической системы переменна, и ее значение зависит от многих факторов, проявление которых невозможно предвидеть заранее, ее характеристику следует отнести к разряду случайных величин. Вследствие рассеяния значений припусков и характеристик свойств материалов заготовок, например, твердости, значения силы резания будут также рассеиваться от PНМ до РНБ. Если при этом учесть, что значения жесткости технологической системы случайны и подлежат рассеянию от j НМ до j НБ, то даже при стабильном рассеянии значений силы резания, значения поля рассеяния
Рис.10. Иллюстрация формирования полей рассеяния упругих перемещений в технологической системе Лекция 6
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 562; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.211.135 (0.008 с.) |




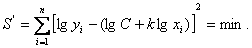
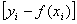 в выражении для S есть отклонение по ординате i – ой экспериментальной точки от заменяющей (аппроксимирующей) кривой. Квадраты отклонений берутся, чтобы компенсировать знаки «-» отклонений.
в выражении для S есть отклонение по ординате i – ой экспериментальной точки от заменяющей (аппроксимирующей) кривой. Квадраты отклонений берутся, чтобы компенсировать знаки «-» отклонений. является математической моделью объекта исследования (здесь процесса резания). Поэтому после получения численных значений C и k необходимо проверить степень соответствия (адекватность) принятой математической модели описываемому объекту. Проверку адекватности производят, например, по F-критерию Фишера. Если принятая аппроксимирующая функция не удовлетворяет критерию Фишера, то она должна быть заменена другой.
является математической моделью объекта исследования (здесь процесса резания). Поэтому после получения численных значений C и k необходимо проверить степень соответствия (адекватность) принятой математической модели описываемому объекту. Проверку адекватности производят, например, по F-критерию Фишера. Если принятая аппроксимирующая функция не удовлетворяет критерию Фишера, то она должна быть заменена другой.


 , которая описывает влияние на силу PZ всех факторов процесса резания, остававшихся постоянными при проведении обеих серий экспериментов, т.е. всех факторов, кроме подачи и глубины резания. Общая формула превращается в частные, если в нее подставить соответственно или
, которая описывает влияние на силу PZ всех факторов процесса резания, остававшихся постоянными при проведении обеих серий экспериментов, т.е. всех факторов, кроме подачи и глубины резания. Общая формула превращается в частные, если в нее подставить соответственно или  , при которой проводилась первая серия экспериментов, или
, при которой проводилась первая серия экспериментов, или  , при которой проводилась вторая серия экспериментов:
, при которой проводилась вторая серия экспериментов:
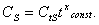

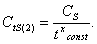


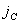 равна:
равна:
 – радиальная составляющая силы резания;
– радиальная составляющая силы резания; - смещение режущей кромки инструмента (деформация упругой системы).
- смещение режущей кромки инструмента (деформация упругой системы). к приращению перемещения
к приращению перемещения  :
:
 .
.


 – рис. 7.
– рис. 7. необходимо найти производную в данной точке
необходимо найти производную в данной точке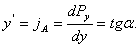
 , образовавшийся вследствие разных глубин резания и, следовательно, разных отжатий в технологической системе, будет меньше
, образовавшийся вследствие разных глубин резания и, следовательно, разных отжатий в технологической системе, будет меньше 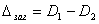 (т.е.
(т.е. 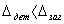 ).
).
 называется уточнением. Оно показывает, во сколько раз в результате обработки уменьшилась погрешность заготовки. Уточнение характеризует жесткость технологической системы:
называется уточнением. Оно показывает, во сколько раз в результате обработки уменьшилась погрешность заготовки. Уточнение характеризует жесткость технологической системы:
 - константа (постоянная силы резания).
- константа (постоянная силы резания).  – подача.
– подача.
 и координаты его середины
и координаты его середины  не будут оставаться постоянными – рис.10. Участок диаграммы между кривыми j НМ и j НБ на этом рисунке представляет собой поле
не будут оставаться постоянными – рис.10. Участок диаграммы между кривыми j НМ и j НБ на этом рисунке представляет собой поле  рассеяния значений жесткости технологической системы.
рассеяния значений жесткости технологической системы.



