
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Участка при достижении максимальной загрузки технологического оборудованияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Постановка задачи. Имеется m – станков (m – групп станков), на которых могут быть изготовлены n – типов деталей. Трудоемкость обработки j - ой детали на i – м станке составляет
Таблица 14 Требуется определить количество деталей каждого наименования Математическая модель для решения задачи: Ограничения:
...
Управляемые параметры:
Целевая функция:
Задача решается методом линейного программирования. При этом следует иметь в виду следующее. Количество ограничений вида (39) - (41) в математической модели должно строго равняться количеству станков (групп станков) участка. При решении задачи с помощью компьютера количество станков (групп станков), а также типов деталей практически не ограничено и определяется только возможностями компьютера и соответствующей программы. При решении задачи вручную с применением графо-аналитического метода количество типов станков (групп станков) также не ограничено, но их увеличение естественным образом приведет к увеличению времени расчетов. Количество же типов деталей не должно превышать двух, т.к. в противном случае невозможно будет на плоскости выполнить необходимые графические построения. Пример. Исходные данные для примера в таблице 15.
Таблица 15
Обозначим через Математическая модель для решения данной задачи запишется следующим образом: Ограничения (по фонду времени работы оборудования):
Целевая функция (суммарное время работы всех групп оборудования):
Требуется найти значения Решим задачу графо – аналитическим методом. Графическая иллюстрация решения задачи приведена на рис. 27.
Рис.27. Графическая иллюстрация решения задачи Вычисления для построения ограничений (44) – (46):
Направления допустимости ограничений (44) – (46) – «вниз – влево». Ограничения (47) и (48) – это оси координат. Направления их допустимости – «вправо» и «вверх». Для нахождения точки касания границы ОДР прямой линией, определяющей целевую функцию, построим сначала произвольную прямую для целевой функции, приравняв ее выражение к произвольному числу в пределах масштаба построений, например к 1500:
Проведя прямую линию, параллельную данной, находим точку касания ее границы ОДР – это точка А. Для нахождения ее координат (точки пересечения ограничений 45 и 46) решаем следующую систему уравнений:
Т.е. окончательно Максимальное значение целевой функции (максимальная загрузка оборудования участка) при оптимальных значениях искомых параметров составит:
Задача о минимальной загрузке оборудования Эта и последующие задачи в данной лекции приводятся на уровне постановки задачи и формирования математической модели для ее решения. Все они решаются методами линейного программирования [1]. Имеется m станков, на которых могут быть изготовлены n типов деталей. Производительность i - го станка при изготовлении детали j - го типа составляет Cij. Величины плановых заданий Aj на изготовление j - ой детали и ресурс времени Bi работы i - го станка приведены в таблице 16.
Таблица 16
Требуется, учитывая ресурсы времени работы каждого станка распределить задания между станками таким образом, чтобы общее время работы всех станков было минимальным. Пусть tij - время изготовления j - ой детали i - м станком. Составим ограничения по ресурсу времени для каждого станка:
Условия выполнения плановых заданий имеют вид:
Решение поставленной задачи состоит в минимизации линейной целевой функции (суммарного времени)
при ограничениях (49), (50) и условии, что все переменные
Задача об оптимальном распределении деталей По станкам Пусть некоторая машина состоит из
Пусть
Общее количество деталей
Общее количество комплектов деталей, необходимых для сборки машины, равно общему количеству какой-либо одной детали, имеющей, например, номер 1. Поэтому решение задачи заключается в максимизации линейной функции
при ограничениях (52), (53) с дополнительным условием, что все переменные Найденные оптимальные значения
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 839; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.234.110 (0.012 с.) |

 , час. Известны фонды времени работы каждого станка (группы станков) – B i. Исходные данные для решения задачи представлены в таблице 14.
, час. Известны фонды времени работы каждого станка (группы станков) – B i. Исходные данные для решения задачи представлены в таблице 14.
 , при обработке которых достигается максимальная загрузка оборудования участка.
, при обработке которых достигается максимальная загрузка оборудования участка.



 .
.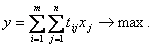

 количество деталей типа D1, через
количество деталей типа D1, через  количество деталей типа D2.
количество деталей типа D2.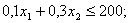









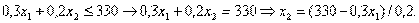










 .
. различных видов деталей, которые мы пронумеруем числами
различных видов деталей, которые мы пронумеруем числами  . Имеется
. Имеется 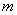 типов различных станков, причем количество станков
типов различных станков, причем количество станков 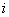 - го типа равно
- го типа равно  . Детали могут быть изготовлены на станках разного типа. Производительность станка
. Детали могут быть изготовлены на станках разного типа. Производительность станка  - ой детали составляет
- ой детали составляет  . После изготовления детали поступают на сборку. Требуется закрепить станки за деталями так, чтобы в единицу времени получать максимальное количество машин.
. После изготовления детали поступают на сборку. Требуется закрепить станки за деталями так, чтобы в единицу времени получать максимальное количество машин. - количество станков
- количество станков  :
:
 . В каждой машине имеется ровно одна деталь с номером
. В каждой машине имеется ровно одна деталь с номером  . Поэтому, для того чтобы не было изготовлено лишних и не было дефицитных деталей, должны выполняться условия комплектности:
. Поэтому, для того чтобы не было изготовлено лишних и не было дефицитных деталей, должны выполняться условия комплектности:

 .
. этой задачи не обязательно целые числа. Например,
этой задачи не обязательно целые числа. Например,  означает, что на двух станках первого типа в течение единицы времени будут изготовлять деталь с номером 1, тогда как третий станок того же типа будет работать лишь половину указанного времени.
означает, что на двух станках первого типа в течение единицы времени будут изготовлять деталь с номером 1, тогда как третий станок того же типа будет работать лишь половину указанного времени.


