Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
На основе динамических характеристик станковСодержание книги
Поиск на нашем сайте
Материалы этой части лекции взяты из работ к.т.н., доцента кафедры «Технология автоматизированного машиностроения» ИГЭУ Минеева А.С. и его дипломника Таланова П.В. Рассмотрим эти вопросы на примере исследования точности плоскошлифовального станка. Сначала разрабатывается расчетная схема упругой системы станка, которая представляет собой многомассовую модель. Для этого станок разбивается на ряд узлов, каждый из которых представляет собой отдельную массу. Кроме этого какая-либо деталь станка принимается как деталь условно бесконечной массы, к которой «привязываются» все остальные массы. Расчетная схема упругой системы плоскошлифовального станка представляет собой четырехмассовую модель. В качестве детали условно бесконечной массы принята станина, к которой «привязаны» все остальные массы (рис. 11) [4]. На данном рисунке приняты следующие обозначения: 1. шпиндель; 2. шпиндельная бабка; 3. продольный стол; 4. поперечный стол; 5. станина; М1, М2, М3, М4 – приведенные массы шпинделя, шпиндельной бабки, продольного стола, поперечного стола; С1, С2, С3, С4 – жесткости; Н1, Н2, Н3, Н4 – коэффициенты демпфирования;
VЗ – скорость продольного перемещения заготовки.
Рис. 11. Расчетная схема упругой системы плоскошлифовального станка
Взаимодействие между отдельными массами описывается, как правило, двумя видами связей: 1. упругими связями, которые характеризуются жесткостью; 2. демпфирующими связями, которые характеризуются коэффициентами демпфирования. Чтобы лучше понять характер взаимодействия масс, можно привести пример работы подвески автомобиля. В ней пружина осуществляет упругую связь, а амортизатор является демпфером. Иногда, рассматривая взаимодействие масс, учитывают третью связь, которая называется инерционной, которая как и две предыдущие также зависит от массы узлов. Все три вида связей зависят и от величины перемещения узла, от его скорости и ускорения. Инерционные связи в данной модели мы рассматривать не будем [20]. Здесь исследуется механизм образования непрямолинейности, поэтому считают, что данная четырехмассовая упругая система имеет свободу перемещения вдоль оси Y. Следовательно, в качестве возбуждающей силы будет рассматриваться только радиальная составляющая сила резания. Т.к. смещение упругой системы необходимо рассматривать только вдоль оси Y, приведению выше на рис. 11 расчетную схему нужно заменять эквивалентной схемой. Динамическая модель эквивалентной упругой системы плоскошлифовального станка приведена на рис. 12. На данном рисунке приняты следующие обозначения: СY1, CY2, CY3, CY4 – жесткости в направлении оси Y; HY1, HY2, HY3, HY4 – коэффициенты демпфирования в направлении оси Y. Основой построения математической динамической модели является уравнение колебаний одномассовой упругой системы (рис.13). Это уравнение представляет собой дифференциальное уравнение второго порядка:
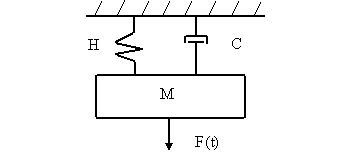
На рис.12. и в данном уравнении приняты следующие обозначения: M – масса, H – коэффициент демпфирования, C – жесткость,
Рис.12. Динамическая модель эквивалентной упругой системы плоскошлифовального станка
Рис.13. Динамическая одномассовая модель
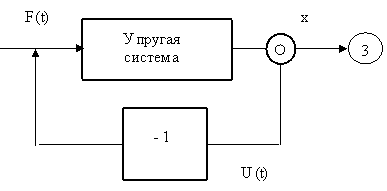
Смысл понятия «обратная сила» заключается в следующем – рис. 14 (на нем буквой «З» обозначена заготовка).
Рис.14. Иллюстрация понятия «обратная сила»
Под действием силы F (t) возникает смещение x упругой системы станка и, как следствие, уменьшение глубины резания, отсюда сила F (t) уменьшается на величину U (t) [34]. Итак, необходимо определить геометрическую сумму смещений
Имея данные об упругих перемещениях несущей системы (шпинделя относительно детали) за n – е количество оборотов шпинделя можно определить величину непрямолинейности поверхности детали, получаемую после шлифования. При шлифовании поверхностей на плоскошлифовальных станках образуется погрешность профиля плоской поверхности в продольном сечении (непрямолинейность), которая имеет следующую природу – см. рис. 15.
Рис.15. Механизм образования непрямолинейности шлифуемой поверхности
На рис.15: 1 – траектория упругих приведенных перемещений оси вращения шпинделя, 2 – профиль продольного сечения плоской поверхности. Деталь рассматривается как неподвижная, а все упругие перемещения узлов станка приводятся к шпинделю. В системе координат шпинделя XшпO1Yшп траектория перемещения торца шлифовального круга имеет форму идеальной окружности радиусом R, центр которой лежит на оси вращения шпинделя. Однако, траектория перемещения оси шпинделя в координатах детали имеет форму сложной кривой 1. Это вызвано неравномерной жесткостью узлов, наличием упругих люфтов в стыках и т.д. Таким образом, траектория движения торца шлифовального круга, полученная при его вращении, образуется при сложении двух движений: 1. Вращательного движения круга вокруг оси шпинделя. 2. Перемещения оси шпинделя по траектории 1 (смещение систем координат XшпO1Yшп и XoOYo). Поэтому траектория движения торца шлифовального круга будет отличаться от идеальной. И это, в свою очередь, определит образование непрямолинейности шлифуемой поверхности. Шлифовальному кругу сообщается круговое движение Vк, детали - продольное движение Vз. В процессе резания возникает сила резания, составляющая P Y которой вызовет деформацию замкнутой технологической системы станка на величину y1, поэтому t ф = t – y 1. Кроме этого на глубину шлифования оказывает влияние и перемещение заготовки вдоль оси X. Оно имеет скачкообразный характер. В момент выхода шлифовального круга из контакта с заготовкой упругая система станка «выбирает» деформацию технологической системы y1. В момент врезания круга в заготовку глубина резания t ф’ = t. Все это вместе взятое определяет характер образования непрямолинейности шлифуемой поверхности. Для реализации имитационного моделирования процесса шлифования был применен программно – методический комплекс МИК (моделирования и конструирования), разработанный в ИГЭУ. При его применении модель динамического процесса представляется в виде структурной модели. Затем с помощью специального языка вводятся параметры модели и осуществляется компьютерный эксперимент. Лекция 7-8
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 427; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.67.237 (0.006 с.) |

 - вектор радиальной составляющей силы резания;
- вектор радиальной составляющей силы резания;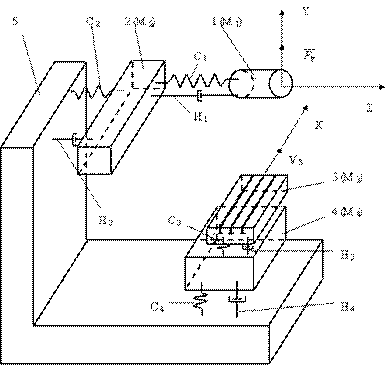
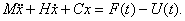
 – возбуждающая сила, действующая в данном направлении, t – время, x - перемещение,
– возбуждающая сила, действующая в данном направлении, t – время, x - перемещение, 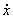 - скорость,
- скорость,  - ускорение,
- ускорение,  - «обратная сила».
- «обратная сила».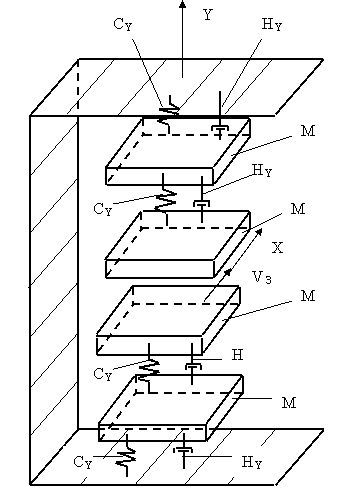
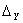 эквивалентной упругой системы вдоль оси Y, которое определяет суммарное смещение оси вращения шпинделя от прямолинейного движения
эквивалентной упругой системы вдоль оси Y, которое определяет суммарное смещение оси вращения шпинделя от прямолинейного движения