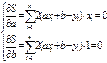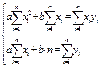Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел функции и его свойства
Предел функции и его свойства Определение Коши используется для обоснования существования предела, а опред-ие Гейна – для обоснования отсутствия предела. Свойства предела: предел единственен и фун-ия в некоторой окрестности предельной точки ограничена. Определение пределов по Гейне. Число А назывется пределом функции f(x) в т x0, если для для любой сходящейся к x0 последовательности (1) значений x, отличных от x0 соответствует последовательность (2), сходящаяся к числу А. lim x→x0 f(x) = A (1) f(x)=c; любое x0 x1, x2, x3…→x0 c, c, c,c…→c limx→x0c=c (2) f(x)=x; любое x0 x1; x2; x3…→x0 x1; x2; x3…→x0 limx→x0x=x0 Определение пределов по Коши. Число А называется пределом функции f(x) в т x0, если для любого ε>0 δ=δ(ε), что ля всех x, удовлетворяющих условию или приним. δ – окрестности х0 |x-x0|<δ x≠x0 |f(x)-A|<ε -δ<x-x0<δ -δ+x0<x<δ+x0
1) Предел постоянной величины Предел постоянной величины равен самой постоянной величине:
2)Предел суммы Предел суммы двух функций равен сумме пределов этих функций:
3) Предел произведения функции на постоянную величину Постоянный коэффициент можно выносить за знак предела:
4)Предел произведения Предел произведения двух функций равен произведению пределов этих функций:
5)Предел частногоПредел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
если Односторонние пределы. Существование предела в точке Число А называется правым(левым) пределом функции f(x), если для любого ε>0 существует δ=δ(ε), что для всех x, отвеч неравенству x0<x<x0+δ (x0-δ<x<x0) => |f(x)- A|<ε f(x) всегда имеет предел в т х0 тогда и только тогда, когда в этой точке существует как правый так и левый пределы, при этом они равны. Сущ-ие предела в точке. Число А назыв. пределом фун-ии f(x) при х, стремящемся к х0 (или точке х0), если для любого, даже сколь угодно малого положительного числа ε>0, найдётся такое положительное число δ>0 (зависящее от ε, δ=δ(ε)), что для всех х, не равных х0 и удовлетворяющее условию Обозначается
Теоремы о пределах функций *пусть f(x) g(x) имеют в точке х0 пределы, соотв В и С lim x→x0f(x)=B lim x→x0g(x)=C f(x)±g(x)=B+C
f(x)*g(x)=B*C f(x)/g(x) (если g(x)≠0)=B/C Следствие Постоянный множитель можно выносить за знак предела *пусть функции f(x) g(x) k(x) оперделены в некоторой окрестности т х0 за искл самой х0 *пусть функции f(x) и k(x) имеет в точке х0 предел А и пусть имеет место неравенство f(x)≤g(x)≤k(x), тогда limg(x)x→x0=A *будем говорить, что f(x)/g(x) есть неопределенность вида 0/0 или бесконечность/бесконечность если числитель и знаменатель одновременно стремятся к 0 или бесконечности limx→бесконечностиPn(x)/Qm(x)= 1)если m=n отношение коэф при х в макс степени 2)Если n>m –бесконечность 3)если n<m 0 * фун-ия не может иметь более одного предела
Сравнение бесконечно больших и бесконечно малых функций Функция αn называется бесконечно малой функцией при x→x0, если ее предел равен 0. Если α(x) и β(x) – бесконечно малые функции и limx→x0 β(x)/α(x)=0, то функция β(x) называется бесконечно малой функцией высшего порядка малости относительно α(x), что записывается в виде β=o(α). Если limx→x0 β(x)/αk(x)=A (отличное от 0 конечное число), то β(x) называется бесконечно малой функцией k-го порядка малости относительно α(x). Если limx→x0 β(x)/α(x)=1, то β(x) и α(x) называются эквивалентными бесконечно малыми функциями: β(x)~α(x).
Первый и второй замечательные пределы Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, называется первым замечательным пределом. Этот предел равен единице. Предел последовательности называется вторым замечательным пределом. Этот предел равен числу e: Понятие производной. геометрический и физический смысл. Производной фун-ии
Нахождении производ. фун-ии назыв. дифференцированием этой фун-ии. Геометрич. смысл произв-ой: производная Физич. смысл производной: производная пути по времени
Теоремы о производных Сформулируем некоторые теоремы о производных. Теорема. Если существуют производные
Следствие. Теорема. Если функция в точке Обратное неверно. На рис. 30 изображена непрерывная функция, у которой в точке Теорема о производной сложной функции. Пусть функция Короче:
Теорема Ролля Пусть функция y=f(x) определена и непрерывна на отрезке [a,b], дифференцируема ∀x ∈(a,b) и f(a)=f(b), тогда существует точка x=c ∈(a,b), в которой f'(c)=0.
Теорема Лагранжа Пусть функция y=f(x) определена и непрерывна на отрезке [a,b], дифференцируема ∀x ∈(a,b), тогда существует точка x=c∈(a,b), такая, что выполняется условие f(b)-f(a)=f’(c)(b-a).
Теорема Коши Пусть функции y=f(x) и y=g(x) непрерывны, определены на отрезке [a,b] и дифференцируемы ∀x ∈(a,b). Пусть также g'(x)≠0, тогда существует точка x=c∈(a,b), такая, что для нее выполняется условие f(b)-f(a)/g(b)-g(a)=f’(c)/g’(c).
20. Правила Лопиталя раскрытия неопределенностей: 1) Если limxàx0f(x)=limxàx0φ(x)=0, то limxàx0f(x)/φ(x)=(0/0)=limxàx0f’(x)/φ’(x) при условии, что предел в правой части выражения существует; аналогично, если limxàx0f'(x)=limxàx0φ’(x)=0, то limxàx0f’(x)/φ’(x)=(0/0)=limxàx0f’’(x)/φ’’(x) при условии, что предел в правой части существует и т.д. 2) Если limxàx0f(x)=limxàx0φ(x)=∞, то limxàx0f(x)/φ(x)=(∞/∞)=limxàx0f’(x)/φ’(x) при условии, что предел в правой части выражения существует; аналогично, если limxàx0f(x)=limxàx0φ(x)=∞, то limxàx0f(x)/φ(x)=(∞/∞)=limxàx0f’(x)/φ’(x) при условии, что предел в правой части существует, и т.д.
21. Формула тейлора где
Точки перегиба Если в точке M(x0, f(x0)) графика функции y=f(x) выпуклость вверх меняется на выпуклость вниз или наоборот, то точка M(x0, f(x0)) называется точкой перегиба. Теорема (необходимое условие точки перегиба). Если в точке M(x0, f(x0)) график функции y=f(x) имеет точку перегиба, а сама функция имеет непрерывную вторую производную, тогда f''(x) в точке x0 обращается в 0, т.е. f’’(x0)=0. Точки графика функции, в которых вторая производная равна 0 или не существует, называются критическими точками II рода. Теорема (достаточное условие точки перегиба). Пусть функция y=f(x) имеет вторую производную в окрестности точки x0 и пусть в самой точке f''(x0)=0 или f’’(x0) не существует. Тогда, если в указанной окрестности f''(x) имеет разные знаки слева и справа от точки x0, график функции имеет перегиб в точке M(x0, f(x0)).
Асимптоты Прямая линия L называется асимптотой графика функции y=f(x), если расстояние от точки M(x,y), лежащей на кривой, до прямой L стремиться к нулю при неограниченном удалении этой точки от начала координат (т.е. при стремлении хотя бы одной из координат точки к бесконечности). Существуют вертикальные, горизонтальные и наклонные асимптоты. Если limxàaf(x)=+∞ или limxàaf(x)= - ∞, то прямая x=a является вертикальной асимптотой графика функции y=f(x). Если limxà+∞f(x)=b или limxà-∞f(x)=b, то прямая y=b является горизонтальной асимптотой графика функции y=f(x). Прямая y=kx+b является наклонной асимптотой графика функции y=f(x), если существуют одновременно пределы:
k=limxà+∞f(x)/x, b=limxà+∞(f(x)-kx) или k=limxà-∞f(x)/x, b=limxà-∞(f(x)-kx).
Производная неявной функции Если функция y=y(x) задана неявно уравнением F(x,y)=0, F(x,y) — дифференцируемая функция и F 'y(x, y) не равен 0, то производная y'(x) вычисляется по формуле y'(t) = - F'x(x, y) / F'y(x, y) (с тремя переменными еще)
Производная по направлению Пусть z=f(x, y) определена в некоторой окрестности точки M(x, y), пусть l0=(cosα, cosβ) – единичный вектор, задающий направление прямой L, проходящей через точку M(x, y). Выберем на прямой L точку M1(x1, y1)= M(x, y)+τ*l0. Рассмотрим приращение функции ∆z=z(M1)-z(M)=f(x+ τ cosα, y+τ cosβ)-f(x, y) в точке M(x, y). Предел отношения limτ→0 f(x+ τ cosα, y+τ cosβ)-f(x, y)/τ, если он существует, называется производной функции z=f(x, y) в точке M(x, y) по направлению l0=(cosα, cosβ) и обозначается ∂z/∂l. Если функция z=f(x, y) имеет в точке M(x, y) непрерывные частные производные, то в этой точке существует и производная по любому направлению, исходящему из точки M(x, y); вычисляется эта производная по формуле ∂z/∂l=∂z/∂x* cosα+∂z/∂y* cosβ, где cosα и cosβ – направляющие косинусы вектора l0.
36. Градиентом функции z=f(x, y) в точке M(x, y) называется вектор с началом в точке M0, координаты которого равны соответствующим частным производным ∂z/∂x и ∂z/∂y, вычисленным в точке M(x, y). Градиент обозначается grad z=(∂z/∂x, ∂z/∂y). Аналогично определяются производная по направлению и градиент для функции трех переменных u=f(x,y,z) в точке M(x, y, z): ∂u/∂l=∂u/∂x*cosα+∂u/∂y*cosβ+∂u/∂z*cosγ; grad u(M)=(∂u/∂x, ∂u/∂y, ∂u/∂z), где cosα, cosβ, cosγ – направляющие косинусы единичного вектора l0. Градиент есть вектор, указывающий направление наибольшего возрастания функции u=f(M).
Условный экстремум 1) Усл-ый экстремум (метод множ-ей Лагранжа): Постановка задачи: Найти экстремумы ф-ии Z=f(x,y) при усл, что φ(x,y)=0. Составляют ф-ию Лагранжа: L=f(x,y) + η φ(x,y); η – множ-ль Лагранжа. Для того, чтобы найти т экстремума, находят стац-е точки ф-ии Лагранжа, т.е. решают систему:
Достат-ое усл экстремума: Если опред-ль ∆>0, то экстр-м есть и при том max; Если ∆<0 => экст-м есть – min
вычисленный в точке (x0, y0, λ 0) (стац т). Метод наименьших квадратов. (x1; y1) (x2; y2) (xn; yn)
Подобрать теоретич. прямую вида y=ax+b "наилучшим образом" согласующуюся с этими данными. δi=yi теор – yi эмпирич; МНК:∑(δi)2→min
Предел функции и его свойства Определение Коши используется для обоснования существования предела, а опред-ие Гейна – для обоснования отсутствия предела.
Свойства предела: предел единственен и фун-ия в некоторой окрестности предельной точки ограничена. Определение пределов по Гейне. Число А назывется пределом функции f(x) в т x0, если для для любой сходящейся к x0 последовательности (1) значений x, отличных от x0 соответствует последовательность (2), сходящаяся к числу А. lim x→x0 f(x) = A (1) f(x)=c; любое x0 x1, x2, x3…→x0 c, c, c,c…→c limx→x0c=c (2) f(x)=x; любое x0 x1; x2; x3…→x0 x1; x2; x3…→x0 limx→x0x=x0 Определение пределов по Коши. Число А называется пределом функции f(x) в т x0, если для любого ε>0 δ=δ(ε), что ля всех x, удовлетворяющих условию или приним. δ – окрестности х0 |x-x0|<δ x≠x0 |f(x)-A|<ε -δ<x-x0<δ -δ+x0<x<δ+x0
1) Предел постоянной величины Предел постоянной величины равен самой постоянной величине:
2)Предел суммы Предел суммы двух функций равен сумме пределов этих функций:
3) Предел произведения функции на постоянную величину Постоянный коэффициент можно выносить за знак предела:
4)Предел произведения Предел произведения двух функций равен произведению пределов этих функций:
5)Предел частногоПредел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
если
|
||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 2289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.149.148 (0.012 с.) |
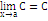


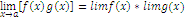

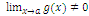
 , выполняется неравенство
, выполняется неравенство 
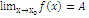 или
или 
 , то это бесконечно малые фун-ии одного порядка
, то это бесконечно малые фун-ии одного порядка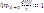


 назыв. предел отношения приращения фун-ии к приращению независимой переменной при стремлении последнего к нулю (если этот предел сущ-ет):
назыв. предел отношения приращения фун-ии к приращению независимой переменной при стремлении последнего к нулю (если этот предел сущ-ет):

 есть угловой коэффициент (тангенс угла наклона) касательной, проведённой к кривой
есть угловой коэффициент (тангенс угла наклона) касательной, проведённой к кривой 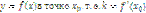
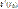 есть скорость точки в момент
есть скорость точки в момент 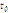 :
: 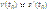
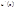 и
и  функций
функций 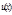 и
и  , то существует
, то существует 
 ;
;
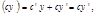 так как
так как  (т.е. постоянный множитель выносится за знак производной.
(т.е. постоянный множитель выносится за знак производной.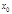 имеет производную, то она в этой точке непрерывна.
имеет производную, то она в этой точке непрерывна. нет производной.
нет производной.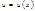 имеет производную в точке
имеет производную в точке 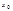 , а функция
, а функция 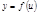 имеет производную в точке
имеет производную в точке 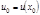 . Тогда сложная функция
. Тогда сложная функция  имеет производную в точке
имеет производную в точке 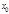 , причем
, причем  .
.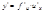 в произвольной точке
в произвольной точке  .
. ,
, - остаточный член формулы Тейлора:
- остаточный член формулы Тейлора: