Тема 23 Методы приближения функций. Основные приложения теории интерполирования
Лекция 23.1 «Методы приближения функций. Основные приложения теории интерполирования»
Учебные вопросы:
1. Интерполяция функций
2. Численное интегрирование
3. Численное дифференцирование
Интерполяция функций
Постановка задачи. В вычислительной практике часто приходится иметь дело с функциями  , заданными в виде таблицы: , заданными в виде таблицы:
В процессе же решения вычислительной задачи могут быть необходимы значения  не только для данного конечного множества значений аргумента не только для данного конечного множества значений аргумента  на отрезке на отрезке  (которые называют узлами интерполирования), но и для его промежуточных значений. В этих случаях можно построить в аналитическом виде (в виде формулы) некоторую непрерывную на (которые называют узлами интерполирования), но и для его промежуточных значений. В этих случаях можно построить в аналитическом виде (в виде формулы) некоторую непрерывную на  функцию функцию 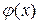 , которая совпадала бы со значениями , которая совпадала бы со значениями 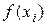 в узлах таблицы и была бы достаточно простой и удобной для вычисления. Построение такой функции в узлах таблицы и была бы достаточно простой и удобной для вычисления. Построение такой функции 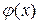 и называется интерполированием функции и называется интерполированием функции  . .
К интерполированию прибегают и в том случае, когда функция  задана в виде формулы, но ее использование сопряжено с большим объемом вычислений и/или их сложностью (например, при вычислении ее значений, численном дифференцировании и интегрировании, решении дифференциальных уравнений и т. д.). задана в виде формулы, но ее использование сопряжено с большим объемом вычислений и/или их сложностью (например, при вычислении ее значений, численном дифференцировании и интегрировании, решении дифференциальных уравнений и т. д.).
Чаще всего в качестве интерполирующей функции 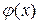 выбираются полиномы выбираются полиномы 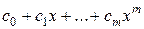 . Это объясняется тем, что они достаточно легко вычисляются и теория интерполяции многочленами хорошо разработана. Доказано, что интерполяционный многочлен для функции . Это объясняется тем, что они достаточно легко вычисляются и теория интерполяции многочленами хорошо разработана. Доказано, что интерполяционный многочлен для функции  , заданной таблично в , заданной таблично в  узлах, существует и единственен, и его степень равна узлах, существует и единственен, и его степень равна  . .
Интерполяционный многочлен Лагранжа. Интерполяционный многочлен в форме
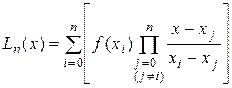 (4.1) (4.1)
называется интерполяционным многочленом Лагранжа. В частности формулы линейной и квадратичной интерполяции по Лагранжу имеют вид:
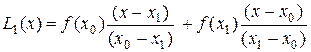 , (4.2) , (4.2)
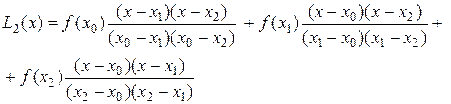 . (4.3) . (4.3)
П р и м е р 1. Построить интерполяционный многочлен Лагранжа по следующим табличным данным:
• В этом случае
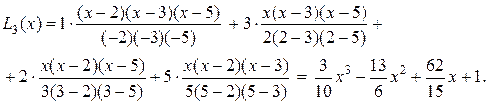 • •
П р и м е р 2. Построить интерполяционный многочлен Лагранжа по следующим данным:
• В этом случае
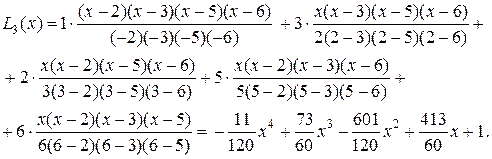 • •
Как видно из приведенных примеров, получение интерполяционных многочленов Лагранжа связано с большой вычислительной работой даже при небольшом числе узлов интерполяции. Кроме того, при добавлении к табличным значениям функции даже одного узла вызывает необходимость проведения всех вычислений заново. Последний недостаток отсутствует у интерполяционного многочлена Ньютона. Он также более удобен для вычислений.
|