
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 21 Итерационные методы решения нелинейных уравнений и их системСодержание книги
Поиск на нашем сайте
Лекция 21.1 «Итерационные методы решения нелинейных уравнений и их систем» Учебные вопросы: 1. Введение. Отделение корней 2. Итерационные методы вычисления корней 3. Непрерывные схемы решения нелинейных уравнений 4. Итерационные методы решения систем нелинейных уравнений
Введение. Отделение корней Введение. Если алгебраические уравнения второй степени (квадратные) решали уже древние греки, то способы решения алгебраических уравнений третьей и четвертой степени были найдены лишь в XVI в. Эти классические способы дают точные формулы решений этих уравнений через их коэффициенты при помощи корней различных степеней (радикалов). Однако эти формулы уже для уравнений третьей степени в общем случае достаточно сложны для вычислений, а для уравнений четвертого порядка требуют настолько громоздких вычислений, что теряют всякую практическую ценность. В отношении алгебраических уравнений пятой и более высоких степеней доказано, что в общем случае их решения не выражаются через коэффициенты при помощи радикалов. Не выражаются в радикалах, например, корни уже такого простого по виду уравнения, как
Сказанное, однако, не означает, что эти уравнения не могут быть решены. В настоящее время в вычислительной математике разработано достаточно много методов численного решения уравнений – алгебраических и неалгебраических (или, как их называют, трансцендентных), позволяющих находить их корни с любой, наперед заданной точностью, что, собственно, и требуется для практических целей. Более того, иногда бывает целесообразнее применить один из этих методов даже в том случае, если корни уравнения выражаются точной формулой, но вычисления по этой формуле трудоемки и/или оценка погрешности этих вычислений затруднена. В этом параграфе будут приведены сведения о некоторых методах численного нахождения действительных корней уравнений
где
где все его коэффициенты При отыскании приближенных значений корней уравнения приходится решать две задачи: 1. отделение корней, т. е. отыскание достаточно малых промежутков, в каждом из которых заключен один и только один корень уравнения; 2. вычисление корней с заданной точностью. 3.2. Отделение корней. В общем случае процесс отделения корней уравнения не может быть алгоритмизирован. Для некоторых типов уравнений (в частности, алгебраических) разработаны специальные приемы отделения корней, позволяющие автоматизировать этот процесс. Нередко отделение корней уравнений выполняется «вручную» с использованием всей возможной информации о функции
Для выделения интервалов, в которых находятся корни уравнения · Если на концах некоторого отрезка · Если при этом · Если на концах отрезка Для алгебраических уравнений (3.2) разработаны специальные методы и приемы отделения корней. Как известно, алгебраическое уравнение степени Найти границы области, в которой расположены все корни Т е о р е м а 1. Все корни уравнения (2) удовлетворяют неравенствам
где Т е о р е м а 2. Пусть в действительном алгебраическом уравнении коэффициент
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 437; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.1.23 (0.007 с.) |


 (3.1)
(3.1) – заданная функция действительного аргумента
– заданная функция действительного аргумента  . В частности, для действительных алгебраических уравнений
. В частности, для действительных алгебраических уравнений  :
: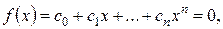 (3.2)
(3.2) – действительные числа.
– действительные числа. отыскания грубых значений корней можно построить график функции
отыскания грубых значений корней можно построить график функции  и найти абсциссы точек пересечения графика с осью
и найти абсциссы точек пересечения графика с осью 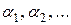 (рис. 3). При отделении корней графическим способом иногда бывает полезным представить сначала уравнение (1) в эквивалентном виде
(рис. 3). При отделении корней графическим способом иногда бывает полезным представить сначала уравнение (1) в эквивалентном виде  и искать точки пересечения графиков функций
и искать точки пересечения графиков функций  и
и  . Например, для уравнения
. Например, для уравнения  вместо построения графика функции
вместо построения графика функции  проще построить графики функций
проще построить графики функций  и
и  (рис. 4).
(рис. 4).
 непрерывная функция
непрерывная функция 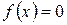 имеет хотя бы один корень.
имеет хотя бы один корень.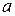 и
и 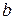 имеется нечетное число корней уравнения
имеется нечетное число корней уравнения  считать
считать  (в том числе и комплексные) алгебраического уравнения (3.2), можно при помощи следующих теорем:
(в том числе и комплексные) алгебраического уравнения (3.2), можно при помощи следующих теорем: , (3.3)
, (3.3) , а
, а  .
.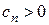 (это всегда можно сделать). Обозначим через
(это всегда можно сделать). Обозначим через 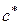 максимум абсолютных величин отрицательных коэффициентов уравнения и пусть первый отрицательный коэффициент в ряду
максимум абсолютных величин отрицательных коэффициентов уравнения и пусть первый отрицательный коэффициент в ряду  есть
есть 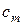 . Тогда все положительные корни уравнения меньше
. Тогда все положительные корни уравнения меньше  , где
, где  (если же отрицательных коэффициентов нет, то нет и положительных корней). Применяя эту теорему к уравнению, в котором произведена замена
(если же отрицательных коэффициентов нет, то нет и положительных корней). Применяя эту теорему к уравнению, в котором произведена замена 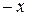 , можно таким же образом получить нижнюю границу отрицательных корней.
, можно таким же образом получить нижнюю границу отрицательных корней.


