Основные характеристики графов

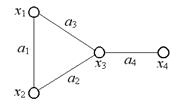
Первая работа по теории графов принадлежащая Эйлеру, появилась в 1736 году. Вначале эта теория была связана с математическими головоломками и играми. Однако впоследствии теория графов стала использоваться в топологии, алгебре, теории чисел. В наше время теория графов находит применение в самых разнообразных областях науки, техники и практической деятельности. Она используется при проектировании электрических сетей, планировании транспортных перевозок, построении молекулярных схем. Применяется теория графов также в экономике, психологии, социологии, биологии.

ГрафG - это математический объект, состоящий из множества вершинX = { x ₁, x ₂,..., x_n } и множества реберA = { a ₁, a ₂,..., a_n }. Таким образом, граф полностью определяется совокупностью множеств X, A: G = (X, A).

Для многих задач несущественно, являются ли ребра отрезками пря­мых или криволинейными дугами; важно лишь то, какие вершины соединяет каждое ребро.

Если ребрам графа приданы направления от одной вершины к другой, то такой граф называется ориентированным. Ребра ориентированного графа называются дугами. Соответствующие вершины ориентированного графа называют началом и концом. Если направления ребер не указываются, то граф называется неориентированным (или просто графом).

Пример 3.1.

На рис. 3.1 изображен неориентированный граф G = (X, A).

X = { x ₁, x ₂, x ₃, x ₄},

A = { a ₁ = (x ₁, x ₂), a ₂ = (x ₂, x ₃), a ₃ = (x ₁, x ₃), a ₄ = (x ₃, x ₄)}.

Рис. 3.1.

Пример 3.2.

На рис. 3.2. изображен ориентированный граф G = (X, A).

X = { x ₁, x ₂, x ₃, x ₄},

A = { a ₁= (x ₁, x ₂), a ₂= (x ₁, x ₃), a ₃= (x ₃, x ₄), a ₄= (x ₃, x ₂)}.

Рис. 3.2.

Граф, имеющий как ориентированные, так и неориентированные ребра, называется смешанным.

Различные ребра могут соединять одну и ту же пару вершин. Такие ребра называют кратными. Граф, содержащий кратные ребра, называется мультиграфом.

Неориентированное ребро графа эквивалентно двум противоположно направленным дугам, соединяющим те же самые вершины.

Ребро может соединять вершину саму с собой. Такое ребро называется петлей. Граф с кратными ребрами и петлями называется псевдографом.

Множество ребер графа может быть пустым. Множество вершин графа не может быть пустым.

Пример 3.3.

На рис. 3.3. изображен ориентированный граф G = (X, A).

X = { x ₁, x ₂, x ₃, x ₄},

A = .

Ри c. 3.3.

Как в случае ориентированного, так и в случае неориентированного ребра говорят, что вершины x и yинцидентны ребру a, если эти вершины соединены a.

Две вершины называются смежными, если они инцидентны одному и тому же ребру. Два ребра называются смежными, если они имеют общую вершину.

Степенью вершины графа называется число ребер, инцидентных этой вершине. Вершина, имеющая степень 0, называется изолированной, а сте­пень 1 – висячей.

Для ориентированного графа множество вершин, в которые ведут дуги, исходящие из вершины х, обозначают G (х), то есть G (х) = { y: (x y) G }. Множество G (x) называют образом вершины x. Соответс­твенно G^{- 1}(у)– множество вершин, из которых исходят дуги, ведущие в вершину у, G^{- 1}(y)= { x: (x, y) G }. Множество G^{- 1}(у)называют прообразом вершины y.

Пример 3.4.

В графе, изображенном на рис. 3.1, концами ребра a ₁являются вер­шины x ₁, x ₂; вершина x ₂инцидентна ребрам a ₁, a ₂; степень вершины x ₃равна3; вершины x ₁и x ₃смежные; ребра a ₁и a ₂смежные; вершина x ₄висячая. В ориентированном графе, изображен­ном на рис. 3.2, началом дуги a ₁является вершина x ₁, а ее концом - вершина x ₂; вершина x ₁инцидентна дугам a ₁и a ₂; G (x ₁) = { x ₂, x ₃}, G (x ₂) = Æ, G^{- 1}(x ₃) = { x ₁}, G^{- 1}(x ₁) = Æ.

Подграфом неориентированного графа G называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G. Аналогично определяется подграф ориентированного графа. Подграф называется собственным, если он отличен от самого графа,

Граф G = (X, A)- полный, если для любой пары вершин x_i и x_j су­ществует ребро (x_i, x_j).

Граф G = (X, A)- симметрический, если для любой дуги (x_i, x_j) существует противоположно ориентированная дуга(x_j, x_i).

Граф G = (X, A) - планарный, если он может быть изображен на плоскости так, что не будет пересекающихся дуг.

Неориентированный граф G = (X, A)– двудольный, если множество его вершин X можно разбить на два такие подмножества X ₁и X ₂, что каж­дое ребро имеет один конец в X ₁, а другой в X ₂.

 

2. Матричные способы задания графов

Для алгебраического задания графов используются матри­цы смежности и инцидентности.

Матрица смежностиA = ( a_ij)определяется одинаково для ориентиро­ванного и неориентированного графов. Это квадратная матрица порядка n, где n - число вершин, у которой

 

a_ij =

Пример 3.5.

Матрица смежности графа, изображенного на рис. 3.1, имеет вид:

A =

Пример 3.6.

Матрица смежности ориентированного графа, изображенного на рис. 3.2, имеет вид:

A =

Матрица смежности полностью задает граф.

Матрицей инцидентностиB = (b_ij) ориентированного графа называет­ся прямоугольная матрица (n ´ m), где n – число вершин, m – число ребер, у которой

b_i =

Для неориентированного графа матрица инцидентности B задается следующим образом:

b_i =

Пример 3.7.

Матрица инцидентности графа, изображенного на рис. 3.1, имеет вид:

B =

Пример 3.8.

Матрица инцидентности ориентированного графа, изображенного на рис. 3.2, имеет вид:

B =

Матрица инцидентности, также, как и матрица смежности, полностью задает граф.

Матрицы смежности и инцидентности удобны для задания графов на ЭВМ.

 

Основные свойства матриц смежности и инцидентности

1. Матрица смежности неориентированного графа является симметрич­ной. Для ориентированного графа это, вообще говоря, неверно.

2. Сумма элементов i - ой строки или i -го столбца матрицы смежности неориентиро­ванного графа равна степени вершины x_i.

3. Сумма элементов i - ой строки матрицы смежности ориентиро­ванного графа равна числу дуг, исходящих из x_i.

4. Сумма элементов i - го столбца матрицы смежности ориентиро­ванного графа равна числу дуг, входящих в вершину x_i.

5. Сумма строк матрицы инцидентности ориентированного графа явля­ется нулевой строкой.

 

Итак, возможны следующие различные способы задания графа:

а) посредством графического изображения;

б) указанием множества вершин и множества ребер (дуг);

в) матрицей смежности;

г) матрицей инцидентности.

 

Изоморфизм графов

Графы G ₁= (X ₁, A ₁)и G ₂= (X ₂, A ₂) изоморфны, если существует взаимно однозначное соответствие между множествами вершин X ₁и X ₂, та­кое, что любые две вершины одного графа соединены тогда и только тог­да, когда соответствующие вершины соединены в другом графе.

Пример 3.9

Графы, изображенные на рис. 3.4 являются изоморфными.

 

Рис. 3.4

 

Изоморфные графы отличаются только нумерацией вершин. Матрицы смежности двух изоморфных графов могут быть получены одна из другой перестановкой строк и столбцов. Чтобы узнать, являются ли два графа изоморфными, нужно произвести все возможные перестановки строк и столбцов матрицы смежности одного из графов. Если после какой-нибудь перестановки получится матрица смежности второго графа, то эти графы изоморфны. Чтобы убедиться, что графы неизоморфны, надо выполнить все n! возможных перестановок строк и столбцов.

 

Лекция 18.2 «Маршруты, циклы, пути в графах»

Учебные вопросы:

1. Маршруты, циклы, пути, контуры в графах

2. Экстремальные пути в графах

3. Деревья