

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
П р и м е р 1. Найти верные и сомнительные цифры в записи приближенного числа 21,327, если абсолютная погрешность составляет 0,032.
• Вычисляем 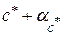 =21,327+0,032=21,359 и =21,327+0,032=21,359 и 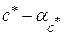 =21,327 –0.032=21,295. Сравнивая полученные числа, устанавливаем, что цифры 2 и 1 – верные, а цифры 3, 2 и 7 – сомнительные. • =21,327 –0.032=21,295. Сравнивая полученные числа, устанавливаем, что цифры 2 и 1 – верные, а цифры 3, 2 и 7 – сомнительные. •
П р и м е р 2. В приближенном числе 26,48 сохранить только верные цифры, если его абсолютная погрешность составляет 0,04.
• Аналогично примеру 1 устанавливаем, что цифры 2 и 6 – верные, а 4 и 8 – сомнительные. Округляя число, получим 26,5, в котором все цифры верные (такая запись числа будет указывать на его предельную абсолютную погрешность равную 0,05, что больше 0,04). • ругляя число, получим 26,5, котором все цифры верные (при такой записи числа его предельная абсолютная пкущая (хорда) (рис.
В вычислительной практике используют также термин число верных (значащих) десятичных знаков (цифр) числа. Под этим понимают число верных цифр после десятичной запятой, не считая нули, стоящие впереди. Так, например, если в числе 0,000304 все цифры верны, то говорят, что оно имеет три верных знака (нули, стоящие слева, не считаются).
Запись приближенных чисел, при которой все цифры должны быть верными, нужно использовать лишь в тех случаях, когда затруднительно указывать наряду с самими числами их погрешности.
Погрешности результатов арифметических операций. Пусть  и и 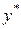 – две приближенные величины, – две приближенные величины, 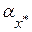 и и  – их абсолютные, а – их абсолютные, а 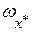 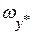 – относительные погрешности, соответственно. Тогда строгий учет погрешностей результатов вычислений может быть произведен при помощи следующих формул: – относительные погрешности, соответственно. Тогда строгий учет погрешностей результатов вычислений может быть произведен при помощи следующих формул:
· 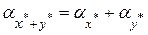 , ,
т. е. при сложении приближенных величин их абсолютные погрешности складываются;
 . .
При сложении приближенных величин относительная погрешность суммы будет заключена между наибольшей и наименьшей относительными погрешностями слагаемых.
· 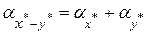 , ,
т. е., как и при сложении, абсолютные погрешности при вычитании приближенных величин складываются;
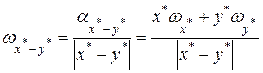 . .
Из последней формулы следует, что если уменьшаемое значительно больше вычитаемого, то знаменатель последней дроби будет близок к  , а сама дробь близка к , а сама дробь близка к 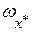 . В этом случае ситуация будет мало отличаться от той, которая имела бы место при сложении этих приближенных величин. Совершенно другая картина получается, если уменьшаемое и вычитаемое имеют близкие значения. В этом случае знаменатель дроби будет очень мал и, следовательно, дробь будет очень велика, что может привести к большой потере верных знаков. Поэтому там, где это возможно, надо стараться избегать вычитания близких по абсолютной величине чисел (например, за счет некоторого преобразования расчетных формул). . В этом случае ситуация будет мало отличаться от той, которая имела бы место при сложении этих приближенных величин. Совершенно другая картина получается, если уменьшаемое и вычитаемое имеют близкие значения. В этом случае знаменатель дроби будет очень мал и, следовательно, дробь будет очень велика, что может привести к большой потере верных знаков. Поэтому там, где это возможно, надо стараться избегать вычитания близких по абсолютной величине чисел (например, за счет некоторого преобразования расчетных формул).
· 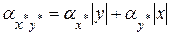 , ,
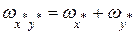 , ,
Т. е. при умножении приближенных величин их относительные погрешности складываются.
· 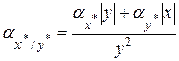 , ,
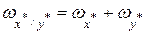 , ,
|