Геометрическое представление комплексных чисел. Тригонометрическая и показательная формы комплексных чисел
Похожие статьи вашей тематики
Комплексное число  удобно изображать точкой на плоскости с удобно изображать точкой на плоскости с
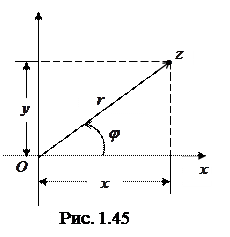 координатами координатами  в прямоугольной декартовой системе координат (рис. 1.45). При этом действительные числа будут изображаться точками оси в прямоугольной декартовой системе координат (рис. 1.45). При этом действительные числа будут изображаться точками оси  , а чисто мнимые – точками оси , а чисто мнимые – точками оси  . Такая плоскость называется комплексной плоскостью, оси . Такая плоскость называется комплексной плоскостью, оси  и и  – соответственно действительной и мнимой осью. Обратно, каждой точке комплексной плоскости с координатами – соответственно действительной и мнимой осью. Обратно, каждой точке комплексной плоскости с координатами  сопоставляется в соответствие вполне определенное комплексное число сопоставляется в соответствие вполне определенное комплексное число  . Это соответствие между множеством всех комплексных чисел и всех точек плоскости взаимно однозначно. . Это соответствие между множеством всех комплексных чисел и всех точек плоскости взаимно однозначно.
Каждой точке  плоскости соответствует вполне определенный вектор – радиус-вектор этой точки, а каждому радиус-вектору, лежащему в плоскости – его конец (рис. 1.45). Поэтому комплексные числа можно представлять также в виде радиус-векторов на плоскости. плоскости соответствует вполне определенный вектор – радиус-вектор этой точки, а каждому радиус-вектору, лежащему в плоскости – его конец (рис. 1.45). Поэтому комплексные числа можно представлять также в виде радиус-векторов на плоскости.
Наряду с представлением комплексных чисел в декартовых координатах часто также используется их представление в полярных координатах. Для этого совместим полярную ось с положительной полуосью  , а полюс – с началом координат; тогда, если обозначить через , а полюс – с началом координат; тогда, если обозначить через  полярный радиус и через полярный радиус и через  полярный угол точки (комплексного числа) полярный угол точки (комплексного числа)  (рис. 1.45), будем иметь: (рис. 1.45), будем иметь:
 , ,  , ,
 (тригонометрическая форма) (1.4.7) (тригонометрическая форма) (1.4.7)
Полярные координаты  и и  точки точки  называются соответственно модулем и аргументом комплексного числа называются соответственно модулем и аргументом комплексного числа  : :
 , (1.4.8) , (1.4.8)
 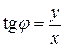 ( (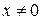 ). (1.4.9) ). (1.4.9)
Если  – действительное число, то его модуль – действительное число, то его модуль  равен его абсолютной величине. равен его абсолютной величине.
Аргумент комплексного числа  определен неоднозначно: определен неоднозначно:  , где , где  – любое целое число, – любое целое число,  – главное значение – главное значение  , в качестве которого обычно выбирают значение, определенное неравенствами , в качестве которого обычно выбирают значение, определенное неравенствами
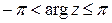 . (1.4.10) . (1.4.10)
С помощью формулы Эйлера
 (1.4.11) (1.4.11)
любое комплексное число  с модулем с модулем  и аргументом и аргументом  можно записать в следующей показательной форме: можно записать в следующей показательной форме:
 . (1.4.12) . (1.4.12)
При условии (1.4.10) для главного значения аргумента числа  будет выполняться будет выполняться  = =  , т. е. , т. е.

Пример. Комплексные числа  и и  записать в тригонометрической и показательной формах. записать в тригонометрической и показательной формах.
 ◄ Находим модули данных комплексных чисел: ◄ Находим модули данных комплексных чисел:  , , 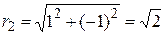 . Главные значения аргументов чисел найдем по абсолютным величинам и знакам . Главные значения аргументов чисел найдем по абсолютным величинам и знакам  и и  : : 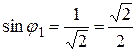 , ,    (число во II –ом квадранте), (число во II –ом квадранте),  , , 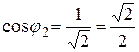   (число в IV –ом квадранте; для выполнения условия (1.4.10) угол отсчитываем от полярной оси по часовой стрелке, т. е. берем его со знаком минус). Геометрическое представление данных чисел приведено на рис. 1.46. Имеем (число в IV –ом квадранте; для выполнения условия (1.4.10) угол отсчитываем от полярной оси по часовой стрелке, т. е. берем его со знаком минус). Геометрическое представление данных чисел приведено на рис. 1.46. Имеем  = = = =   , ,
 = = 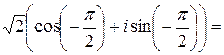
=   ► ►
Если даны 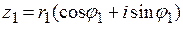 и и 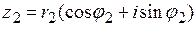 , то , то
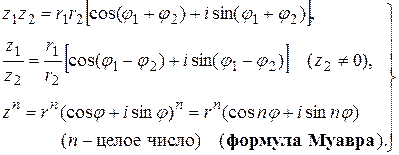 (1.4.13) (1.4.13)
Если комплексные числа заданы в показательной форме:  , ,  , то , то
 (1.4.14) (1.4.14)
Если  – натуральное число и – натуральное число и 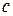 – комплексное число, то – комплексное число, то  (корень (корень  -й степени из -й степени из 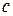 ) есть решение уравнения ) есть решение уравнения  . При . При  существует ровно существует ровно  различных значений корня различных значений корня  -й степени из -й степени из 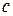 . Они определяются формулами . Они определяются формулами
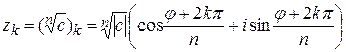 , (1.4.15) , (1.4.15)
где 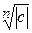 – арифметический корень из положительного числа – арифметический корень из положительного числа 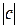 , , 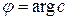 и и  = 0, 1, 2, …, = 0, 1, 2, …,  . Эти значения . Эти значения  располагаются в вершинах правильного располагаются в вершинах правильного  -угольника, вписанного в окружность радиуса -угольника, вписанного в окружность радиуса 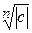 с центром в начале координат. с центром в начале координат.
Пример. Найти все значения  . .
 ◄ Имеем ◄ Имеем 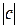 = =  , ,  (рис. 1.47). Так как (рис. 1.47). Так как  , будем иметь три различных значения корня , будем иметь три различных значения корня  , которыми согласно (1.4.15) будут , которыми согласно (1.4.15) будут
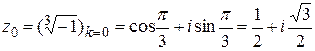 , ,
 , ,
 
 . Эти значения располагаются в вершинах правильного треуугольника, вписанного в окружность радиуса . Эти значения располагаются в вершинах правильного треуугольника, вписанного в окружность радиуса 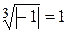 с центром в начале координат (рис. 1.47). Отметим, что корни с центром в начале координат (рис. 1.47). Отметим, что корни  и и  представляют пару комплексно сопряженных чисел, т. е. представляют пару комплексно сопряженных чисел, т. е.  . ► . ►
|