
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контрольная работа № 3. Комплексные числа.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
3.1. Даны комплексные числа 3.2. Даны числа: 3.3. Даны числа 3.4. Решить уравнение
Краткие теоретические сведения для выполнения контрольной работы № 3 и решение типовых задач
Действия над комплексными числами В алгебраической форме
Выражение вида
где х и у – произвольные действительные числа, i – мнимая единица, удовлетворяющая условию Число х называется действительной частью комплексного числа z и обозначается При Два комплексных числа называются равными, если у них равны соответственно действительные и мнимые части:
Комплексные числа называются сопряженными, если у них равны действительные части, а мнимые противоположны по знаку; сопряженные числа обозначают
Определим основные действия над комплексными числами Суммой двух комплексных чисел Разностью комплексных чисел Произведением комплексных чисел Частным от деления
Чтобы разделить число z 1 на z 2 Возведение комплексного числа z в степень n – это нахождение произведения n сомножителей, каждый из которых равен z, т.е.
Пример Даны комплексные числа Вычислить Решение
Тригонометрическая и показательная формы комплексного числа
Комплексное число
r j
0 х= Re z Рис. 1
Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, ось Ох – действительной осью, ось Оу – мнимой осью. Число r – длина радиус-вектора точки
Угол j, который образован вектором Аргумент комплексного числа
где
Аргумент числа Если вектор Если вектор Если Существует несколько подходов к определению аргумента. Один из них состоит в следующем. Если
где Учитывая, что
тригонометрической форма записи комплексного числа.
Используя формулу Эйлера
где Пример Даны комплексные числа:
у
5,5 z 3 z 6 2
-6 z 4
Рис. 2.
1. Найдем модуль и аргумент для комплексного числа
2. Для Следовательно:
3. Для
Следовательно:
4. Для
Следовательно:
5. Для
Следовательно:
6. Для
Следовательно:
7. Для
Следовательно:
8. Для
Следовательно:
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1009; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.5.164 (0.011 с.) |

 и
и  . Вычислить
. Вычислить  .
. ,
,  . Изобразить числа на комплексной плоскости, найти модуль и аргумент, записать в тригонометрической и показательной форме.
. Изобразить числа на комплексной плоскости, найти модуль и аргумент, записать в тригонометрической и показательной форме. . Вычислить
. Вычислить  .
. .
. (1)
(1) , называется алгебраической формой записи комплексного числа.
, называется алгебраической формой записи комплексного числа. , число у называется мнимой частью комплексного числа z и обозначается
, число у называется мнимой частью комплексного числа z и обозначается  .
.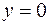 число
число  совпадает с вещественным числом х, если
совпадает с вещественным числом х, если  число
число  называется чисто мнимым.
называется чисто мнимым. .
. .
. и
и 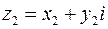 , заданными в алгебраической форме.
, заданными в алгебраической форме. называется комплексное число
называется комплексное число  , т.е. при сложении комплексных чисел складываются действительные и мнимые части соответственно.
, т.е. при сложении комплексных чисел складываются действительные и мнимые части соответственно.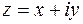 , которое удовлетворяет равенству
, которое удовлетворяет равенству  . Очевидно:
. Очевидно:  . При нахождении разности
. При нахождении разности  из действительной и мнимой частей уменьшаемого z 1 вычитаются соответственно действительная и мнимая части вычитаемого z 2.
из действительной и мнимой частей уменьшаемого z 1 вычитаются соответственно действительная и мнимая части вычитаемого z 2. . Комплексные числа перемножаются как двучлены, при этом учитывается, что
. Комплексные числа перемножаются как двучлены, при этом учитывается, что  .
. называется такое комплексное число z, которое удовлетворяет уравнению
называется такое комплексное число z, которое удовлетворяет уравнению  . Для частного имеет место формула:
. Для частного имеет место формула:
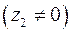 , следует числитель и знаменатель дроби
, следует числитель и знаменатель дроби  умножить на число
умножить на число  , сопряженное знаменателю.
, сопряженное знаменателю.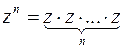 . При возведении в степень n используется правило возведения в степень двучлена
. При возведении в степень n используется правило возведения в степень двучлена 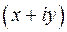 , в общем случае применяется формула бинома Ньютона.
, в общем случае применяется формула бинома Ньютона. .
.
 .
. ,
, ,
, ,
, ,
,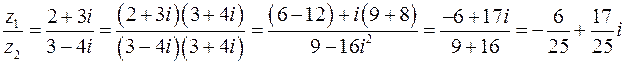 ,
,
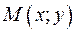 (рис. 1).
(рис. 1). у= Im z
у= Im z

 М (х, у)
М (х, у)

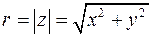 . (2)
. (2) с осью Ох и отсчитываемый от положительного направления оси Ох, называется аргументом комплексного числа и обозначается Arg z.
с осью Ох и отсчитываемый от положительного направления оси Ох, называется аргументом комплексного числа и обозначается Arg z. определен с точностью до слагаемого, кратного
определен с точностью до слагаемого, кратного  :
:
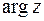 – главное значение аргумента, определяемое условием
– главное значение аргумента, определяемое условием .
. неопределен.
неопределен. .
. .
. , то будем считать, что
, то будем считать, что 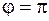 .
. ,
, , получим
, получим - (3)
- (3) , получим показательную форму комплексного числа:
, получим показательную форму комплексного числа: , (4)
, (4) – модуль,
– модуль,  – аргумент комплексного числа.
– аргумент комплексного числа. ,
,  . Изобразить числа на комплексной плоскости, найти модуль и аргумент, записать в тригонометрической и показательной форме.
. Изобразить числа на комплексной плоскости, найти модуль и аргумент, записать в тригонометрической и показательной форме. Решение (рис. 2)
Решение (рис. 2)
 7 z 5
7 z 5

 z 2 z 1
z 2 z 1






 -7 -5,5 -3,5 0 2 6 12,1 х
-7 -5,5 -3,5 0 2 6 12,1 х -2 z 8
-2 z 8 z 7 -12,1
z 7 -12,1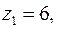
 . Подставляя модуль и аргумент в формулы (3) и (4), получим
. Подставляя модуль и аргумент в формулы (3) и (4), получим .
. имеем:
имеем: 
 .
. имеем:
имеем: 
 .
. имеем:
имеем: 
 .
. имеем:
имеем:

 .
. имеем:
имеем:

 .
. имеем:
имеем: ,
,
 .
. имеем:
имеем:
 .
.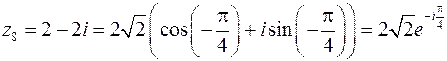 .
.


