
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контрольная работа № 1. Элементы линейной алгебры.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1.1. Найти значение матричного многочлена 1.2. Вычислить определитель двумя способами, по правилу треугольника и разложением по строке (или столбцу): 1.3. Найти матрицу обратную к матрице 1.4. Решить систему линейных алгебраических уравнений тремя способами: по формулам Крамера, с помощью обратной матрицы, методом Гаусса: Краткие теоретические сведения для выполнения контрольной работы № 1 и решение типовых задач
Матрицы и действия над ними Прямоугольная таблица чисел вида
называется матрицей размера m ´ n; здесь m – число строк, n – число столбцов. Числа Если число строк и столбцов матрицы одинаковое Квадратная матрица, в которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной, а диагональная матрица, у которой все элементы, стоящие на главной диагонали равны единице, называется единичной:
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю. Например:
Матрица, все элементы которой равны нулю, называется нулевой и обозначается символом О, например Прямоугольная матрица, в которой каждая строка заменена столбцом с тем же номером, называется транспонированной по отношению к данной матрице, обозначается Очевидно, что Действия над матрицами
Две матрицы одинакового размера называются равными, если их соответствующие элементы равны. А = В, если Суммой двух матриц одинакового размера называется матрица того же размера, все элементы которой равны суммам соответствующих элементов слагаемых матриц. А + В = С, если
Пример 1
Произведением матрицы А на число α называется матрица αА или А α, все элементы которой равны соответствующим элементам матрицы А, умноженным на α.
Пример 2
Матрица
Умножение матриц.
Пусть дана матрица А размера m ´ n и матрица В размера n ´ p.
Для двух матриц А и В, у которых число столбцов первой матрицы равно числу строк второй матрицы, определено понятие произведения матрицы А на В следующим образом: С = А · В, где С есть матрица размера m ´ p,
если
Из определения вытекает следующее правило умножения матриц: чтобы получить элемент, стоящий в i -той строке и j -том столбце произведения двух матриц, нужно элементы i -той строки первой матрицы умножить на соответствующие элементы j –го столбца второй и полученные произведения сложить. Таким образом, чтобы составить первую строку матрицы С нужно перемножить первую строку матрицы А поочередно на все столбцы В; чтобы получить вторую строку произведения С, нужно вторую строку А перемножить последовательно на все столбцы В и т.д. Пример 3
Произведение двух матриц НЕ подчиняется переместительному (коммутативному) закону
в чем можно убедиться на примерах. Кроме того, если произведение АВ определено, то ВА может не иметь смысла. В частных случаях, когда Легко доказать, что единичная матрица Е перестановочна с любой квадратной матрицей А того же порядка, причем А Е = Е А = А. Таким образом, единичная матрица играет роль единицы при умножении. Пример 4 Найти значение матричного многочлена Решение
Определители 2-го и 3-го порядков
Рассмотрим квадратную матрицу 2-го порядка:
Определение. Определителем 2-го порядка, соответствующим матрице А, называется число
Числа а11, а12, а21, а22 называются элементами определителя (они же элементы матрицы А). Элементы а 11, а 22 составляют главную диагональ, а элементы а 21, а 12 – побочную диагональ.
Пусть дана квадратная матрица 3-го порядка:
Определение. Определителем 3-го порядка, соответствующим матрице А, называется число D, которое определяется выражением:
Элементы а 11, а 22, а 33 – расположены на главной диагонали, элементы а 13, а 22, а 31 – на побочной диагонали.
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 585; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.007 с.) |

 , если
, если  ,
,  ,
,  .
. .
. и проверить выполнение равенства
и проверить выполнение равенства  .
. .
.
 (i = 1,2,…, m; j = 1,2,…, n) составляющие матрицу, называются ее элементами. Первый индекс i означает номер строки, второй j – номер столбца.
(i = 1,2,…, m; j = 1,2,…, n) составляющие матрицу, называются ее элементами. Первый индекс i означает номер строки, второй j – номер столбца. , то матрица называется квадратной, порядка n.
, то матрица называется квадратной, порядка n.
 .
. .
. . Например, если
. Например, если 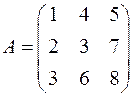 , то
, то  .
.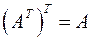 .
. (i = 1,2,…, m; j = 1,2,…, n).
(i = 1,2,…, m; j = 1,2,…, n). (i = 1,2,…, m; j = 1,2,…, n).
(i = 1,2,…, m; j = 1,2,…, n). .
.
 называется противоположной матрице А.
называется противоположной матрице А.


 ,
, , где (i = 1,2,…, m; j = 1,2,…, p).
, где (i = 1,2,…, m; j = 1,2,…, p).

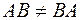 ,
, матрицы называются перестановочными.
матрицы называются перестановочными. , если
, если  ,
,  ,
, 
 .
.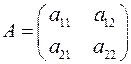
 .
. .
.



