
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Действия над комплексными числами в тригонометрической формеСодержание книги
Поиск на нашем сайте
Рассмотрим два комплексных числа в тригонометрической форме
При перемножении комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются, т.е.
Формула возведения комплексных чисел в натуральную степень:
Деление комплексных чисел, заданных в тригонометрической форме, выполняется по формуле
Модуль частного равен частному от деления модуля числителя на модуль знаменателя, а аргумент частного равен разности аргументов делимого и делителя. В результате умножения и деления чисел может получиться аргумент произведения и частного, не являющийся главным значением. Пример Даны числа Вычислить Решение
Решение уравнений
Пусть требуется извлечь корень n -ой степени из комплексного числа, заданного в тригонометрической Формула извлечения корня из комплексного числа в тригонометрической форме имеет вид
Таким образом, для любого комплексного числа Задача извлечения корня степени n из комплексного числа равносильна решению уравнения вида
Для решения уравнения нужно найти Пример Решить уравнение Решение Задача равносильна нахождению всех значений корня из комплексного числа. В этом случае Определим модуль и аргумент комплексного числа
Следовательно:
Используя формулу извлечения корня, имеем
Придавая k последовательно значения от 0 до 2, выписываем решения уравнения:
Контрольная работа № 4. Предел и производная функции одной переменной.
4. 4.1. Вычислить предел 4.2. Вычислить предел 4.3. Вычислить предел 4.4. В точках 4.5. Найти производную функции 4.6. Найти производную функции 4.7. Найти производную функции 4.8. Найти производную функции, заданной неявно: 4.9. Найти производную функции, заданной параметрически: 4.10. С помощью методов дифференциального исчисления исследовать и построить график функции
Краткие теоретические сведения для выполнения контрольной работы № 4 и решение типовых задач
4.1. Раскрытие неопределенности вида Рассмотрим отношение функций Чтобы раскрыть неопределенность вида
Пример 1
так как при Пример 2
Пример 3
Замечание. Из рассмотренных примеров видно, что предел частного двух многочленов при 4.2. Раскрытие неопределенности вида Рассмотрим отношение функций Чтобы раскрыть неопределенность вида Чтобы раскрыть неопределенность вида
Пример Вычислить предел Решение При
тогда,
Таким образом, получим:
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 749; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 и
и  .
. .
. .
. .
.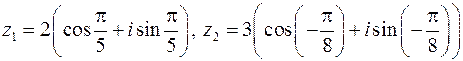 .
. .
.


 форме.
форме. .
.
 имеет n различных корней, точки им соответствующие расположены в вершинах правильного n -угольника, вписанного в окружность радиуса
имеет n различных корней, точки им соответствующие расположены в вершинах правильного n -угольника, вписанного в окружность радиуса  .
. .
. и использовать формулу извлечения корня.
и использовать формулу извлечения корня. .
. .
. :
:
 .
.
 ,
, ,
, .
. .
. .
. .
. и
и  для функции
для функции  установить непрерывность или определить характер точек разрыва.
установить непрерывность или определить характер точек разрыва. .
.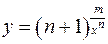
 , применяя метод логарифмического дифференцирования.
, применяя метод логарифмического дифференцирования. .
. .
. .
. .
. . Пусть
. Пусть  – бесконечно большие функции (б.б.ф.) при
– бесконечно большие функции (б.б.ф.) при  , отношение
, отношение  ,
, каждая из дробей
каждая из дробей  стремится к нулю.
стремится к нулю. .
. .
.
 .
. числитель и знаменатель дроби стремится к нулю, т.е. имеет место неопределенность вида
числитель и знаменатель дроби стремится к нулю, т.е. имеет место неопределенность вида  , а квадратный трехчлен
, а квадратный трехчлен  разложим на множители, найдя для этого его корни:
разложим на множители, найдя для этого его корни: ,
, .
.
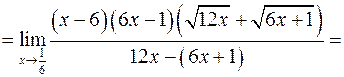

 .
.


