
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциал функции двух переменных
Частным дифференциалом функции выражение выражение
Пример 1 Найти частные дифференциалы функции
Решение
Полный дифференциал функции
Пример 2 Найти дифференциал Решение Найдем частные производные
Подставим частные производные в формулу полного дифференциала, получим
Касательная плоскость и нормаль к поверхности
Прямая линия называется касательной к поверхности в некоторой точке Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную точку Если уравнение поверхности задано неявно, т.е.
Если уравнение поверхности задано в явном виде, т.е.
Нормалью к поверхности называют прямую, перпендикулярную к касательной плоскости в точке касания. Если уравнение поверхности задано неявно, т.е.
Если уравнение поверхности задано в явном виде, т.е.
Пример Составить уравнения касательной плоскости и нормали к поверхности Решение Найдем частные производные
Уравнение касательной плоскости:
Уравнение нормали:
Производная по направлению и градиент
Пусть функция Производная функции
где
Производная по направлению является скоростью изменения функции Абсолютная величина производной по направлению
Градиентом функции
т.е. вектор, проекции которого на координатные оси Ох, Оу, Oz равны соответственно частным производным по х, у, z в точке Градиент U в данной точке по численному значению и по направлению характеризует наибольшую скорость возрастания величины U.
Пример Для функции Решение Градиент находим по формуле
Производная по направлению: где
Контрольная работа № 7. Обыкновенные дифференциальные уравнения.
7.1. Найти общее решение уравнения 7.2. Найти общее решение уравнения 7.3. Найти общее решение уравнения 7.4. Решить задачу Коши: 7.4.1. 7.4.2. 7.5. Решить систему уравнений:
Краткие теоретические сведения для выполнения контрольной работы № 7 и решение типовых задач
ДУ 1-го порядка с разделяющимися переменными Дифференциальное уравнение (ДУ) вида
называется уравнением с разделяющимися переменными. В нем коэффициенты при дифференциалах распадаются на множители, зависящие только от х и только от у.
Путем деления на выражение
Общий интеграл его запишется в виде:
Замечание. Деление на
Пример Найти общее решение уравнения Решение Полагая разделим переменные
или
Размерно-однородные ДУ 1-го порядка
Функция
Пример 1 Рассмотрим функцию
Пример 2 Рассмотрим функцию
ДУ 1-го порядка
называется однородным относительно х и у, если функция Подстановка Замечание. ДУ вида
Пример 3 Найти общее решение уравнения Решение Запишем уравнение в виде Так как для функции Введем подстановку
или
откуда получаем
Разделяя переменные и интегрируя, находим последовательно:
производя обратную замену
или
Линейные ДУ 1-го порядка
Уравнение вида
где Если Одним из методов решения линейных ДУ 1-го порядка является метод Бернулли, согласно которому решение уравнения ищут в виде произведения двух функций
Пример Найти общее решение уравнения Решение Будем искать решение уравнения в виде
Сгруппируем члены, содержащие U в первой степени
Примем за V какое-либо решение уравнения
разделяя в нем переменные, получим
проинтегрируем
так как достаточно выбрать любое отличное от нуля решение, то постоянную не вводим, считая Для нахождения U имеем уравнение
разделяя переменные, получим
Таким образом,
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 3749; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.131.178 (0.192 с.) |
 называется произведение частной производной на соответствующее произвольное приращение независимой переменной:
называется произведение частной производной на соответствующее произвольное приращение независимой переменной: называется частным дифференциалом функции
называется частным дифференциалом функции  по переменной х;
по переменной х; называется частным дифференциалом функции
называется частным дифференциалом функции 
 ,
,  .
. .
. функции
функции  .
. ,
,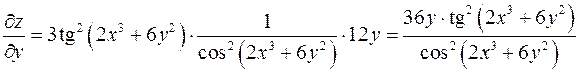 .
.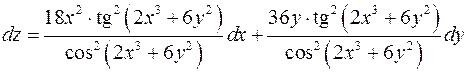 .
. , если она является касательной к какой-либо кривой, лежащей на поверхности и проходящей через точку
, если она является касательной к какой-либо кривой, лежащей на поверхности и проходящей через точку  .
. , то уравнение касательной плоскости к поверхности в точке
, то уравнение касательной плоскости к поверхности в точке 
 .
. .
. .
. в точке
в точке  .
.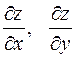 и вычислим их значения в точке
и вычислим их значения в точке  .
. или
или  .
. .
. дифференцируема в точке
дифференцируема в точке  .
. находится по формуле
находится по формуле ,
, – единичный вектор заданного направления
– единичный вектор заданного направления  ,
,  – направляющие косинусы вектора, которые находятся по формулам
– направляющие косинусы вектора, которые находятся по формулам .
. и равный
и равный ,
, в точке
в точке  найти градиент и производную по направлению
найти градиент и производную по направлению  .
. , где
, где тогда
тогда .
. ,
, , тогда
, тогда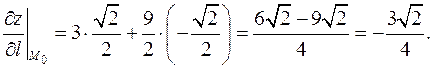
 .
. .
. .
.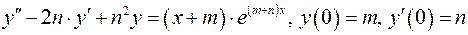 .
. .
. ,
,  .
.
 оно приводится к уравнению с разделенными переменными:
оно приводится к уравнению с разделенными переменными: .
. .
. может привести к потере решений
может привести к потере решений  или
или  , обращающих это произведение в ноль. Среди этих решений могут быть особые решения.
, обращающих это произведение в ноль. Среди этих решений могут быть особые решения.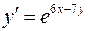 .
. , запишем уравнение в виде
, запишем уравнение в виде  ,
, , проинтегрируем
, проинтегрируем ,
,
 , где
, где  - общий интеграл уравнения.
- общий интеграл уравнения. называется однородной функцией k -го измерения относительно переменных х и у, если при любом допустимом t справедливо тождество
называется однородной функцией k -го измерения относительно переменных х и у, если при любом допустимом t справедливо тождество .
. . Для этой функции
. Для этой функции  , т.е. данная функция
, т.е. данная функция  . Для этой функции
. Для этой функции 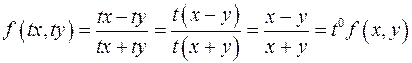 , т.е.
, т.е. 
 преобразует это уравнение в уравнение с разделяющимися переменными.
преобразует это уравнение в уравнение с разделяющимися переменными. будет однородным в том и только в том случае, когда
будет однородным в том и только в том случае, когда  и
и  являются однородными функциями одного и того же измерения.
являются однородными функциями одного и того же измерения. .
.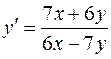 .
. , выполняется условие
, выполняется условие  , то функция
, то функция 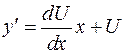 , тогда уравнение примет вид
, тогда уравнение примет вид ,
, ,
, .
.
 ,
, , находим
, находим ,
, - общий интеграл.
- общий интеграл. ,
, и
и 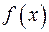 – непрерывные функции, называется линейным ДУ 1-го порядка.
– непрерывные функции, называется линейным ДУ 1-го порядка. , то уравнение называется линейным однородным ДУ (ЛОДУ), если
, то уравнение называется линейным однородным ДУ (ЛОДУ), если  , то уравнение называется линейным неоднородным ДУ (ЛНДУ).
, то уравнение называется линейным неоднородным ДУ (ЛНДУ). . Одну из функций выбирают произвольно, а другую находят из уравнения в зависимости от первой.
. Одну из функций выбирают произвольно, а другую находят из уравнения в зависимости от первой. .
. , тогда
, тогда  . Подставим
. Подставим  и
и 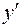 в исходное уравнение, получим
в исходное уравнение, получим .
. .
. ,
, ,
, ,
, .
.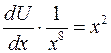 ,
,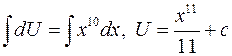 .
.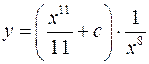 , или
, или  - общее решение уравнения.
- общее решение уравнения.


