
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление пределов с использованием второго замечательного пределаСодержание книги
Поиск на нашем сайте
Одна из форм записи второго замечательного предела
Второй замечательный предел раскрывает неопределенность вида
Пример Вычислить предел
Решение Предел основания
и применим второй замечательный предел:
Непрерывность функции
Пусть функция Определение. Функция
Таким образом, для того чтобы функция 1) функция 2) должны существовать пределы функции 3) эти пределы должны быть равны между собой и равны значению функции Если хотя бы одно из этих условий не выполнено, то говорят, что функция имеет разрыв в точке Точки разрыва следует искать среди точек, не входящих в область определения функции.
Классификация точек разрыва
Определение. Если в точке
или функция не определена, то точка В этом случае функцию можно доопределить в точке
Определение. Если в точке При переходе через точку
Определение. Точка
Пример В точках Решение Область определения функции Исследуем точку если если
Так как односторонние пределы конечны, но не равны между собой, то в точке Исследуем точку если если Так как односторонние пределы равны
Правила дифференцирования
Определение. Производной функции
По определению
Таблица производных
Правила дифференцирования
1. Производная постоянной равна нулю: 2. Теорема. Если каждая из функций 1) 2) 3) Следствие. Постоянный множитель можно выносить за знак производной:
Пример Используя таблицу производных и правила дифференцирования, найти производную функции Решение
Производная сложной функции
Пусть дана сложная функция Теорема. Если функция
Замечание. Теорема может быть обобщена на случай любой конечной цепочки функций. Так, если Пример Найти производную функции Решение Здесь
Метод логарифмического дифференцирования
Метод логарифмического дифференцирования удобен для нахождения производной показательной функции
Пример Найти производную функции Решение Здесь основание и показатель степени зависит от х. Логарифмируем обе части равенства
применяя свойства логарифмов, получим
Продифференцируем обе части последнего равенства по х, рассматривая у как функцию х:
умножим обе части равенства на у и подставим вместо у его выражение
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 474; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

 .
.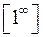 .
. .
.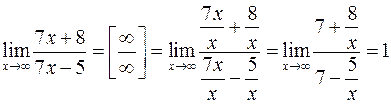 , а показатель степени
, а показатель степени 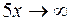 при
при  , т.е. имеет место неопределенность вида
, т.е. имеет место неопределенность вида 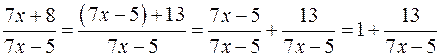

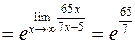 , учитывая, что
, учитывая, что 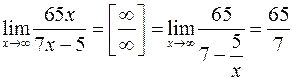 .
. определена в некоторой окрестности точки
определена в некоторой окрестности точки  .
.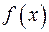 называется непрерывной в точке
называется непрерывной в точке  – значению функции
– значению функции  .
. была непрерывна в точке
была непрерывна в точке 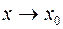 как слева, так и справа, т.е.
как слева, так и справа, т.е. 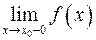 и
и 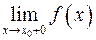 ;
;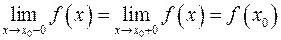 .
.
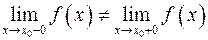 , то точка
, то точка 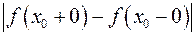 .
.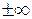 .
. и
и  для функции
для функции 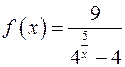 установить характер точек разрыва.
установить характер точек разрыва.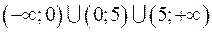 . Данная функция непрерывна во всех точках, кроме точек
. Данная функция непрерывна во всех точках, кроме точек 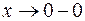 , то
, то 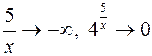 , тогда предел слева
, тогда предел слева 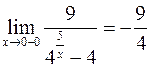 ,
, , то
, то  , тогда предел справа
, тогда предел справа  .
.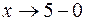 , то
, то 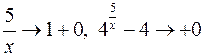 , тогда
, тогда 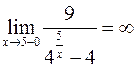 ,
, , то
, то 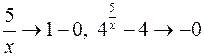 , тогда
, тогда 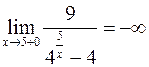 .
.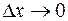 , если он существует.
, если он существует. .
. ,
, 

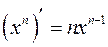
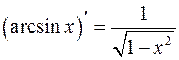

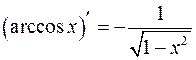
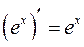
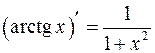
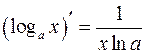
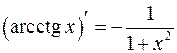
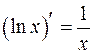
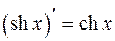

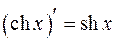
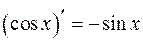
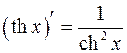
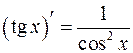

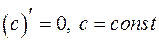 .
.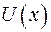 и
и  дифференцируема в данной точке х, то сумма, разность, произведение и частное (частное при условии
дифференцируема в данной точке х, то сумма, разность, произведение и частное (частное при условии  ) так же дифференцируемы в этой точке, причем имеют место формулы:
) так же дифференцируемы в этой точке, причем имеют место формулы: ,
,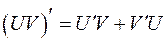 ,
,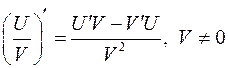 .
. .
.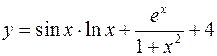 .
.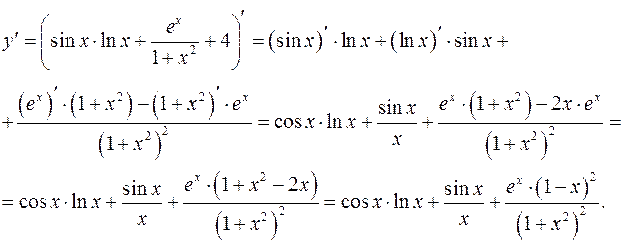
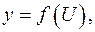 где
где 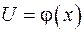 или
или 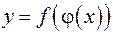 .
. дифференцируема в точке
дифференцируема в точке  , тогда сложная функция
, тогда сложная функция  или
или 
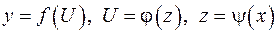 , или
, или 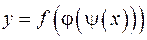 и существуют производные
и существуют производные 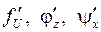 , то
, то 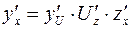 .
.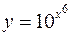 .
.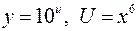 ,
,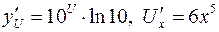 , тогда
, тогда 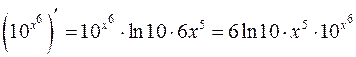 .
. , показательно – степенной функции
, показательно – степенной функции 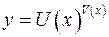 , а также, если функция представляет собой выражение вида
, а также, если функция представляет собой выражение вида 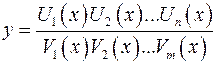 . Этот метод состоит в следующем: данное выражение сначала логарифмируют по основанию е, а затем дифференцируют как тождество, получая уравнение для нахождения производной.
. Этот метод состоит в следующем: данное выражение сначала логарифмируют по основанию е, а затем дифференцируют как тождество, получая уравнение для нахождения производной.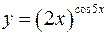 применяя метод логарифмического дифференцирования.
применяя метод логарифмического дифференцирования. ,
,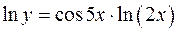 .
.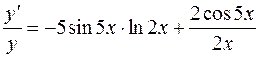 ,
,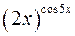 , получим
, получим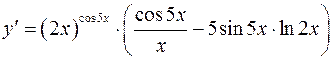 .
.


