
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы электрических цепей.Содержание книги Поиск на нашем сайте Элементы электрических цепей. Электрической цепью называется совокупность устройств, предназначенных для прохождения электрического тока. Электромагнитные процессы в электрических цепях описываются при помощи понятий «ток» и «напряжение». В общем случае электрическая цепь состоит из источников и приемников электрической энергии и промежуточных звеньев, связывающих источники с приемниками. Источники электрической энергии – гальванические элементы, аккумуляторы, термоэлементы, генераторы и другие устройства, в которых происходит процесс преобразования химической, тепловой, механической или другого вида энергии в электрическую. Приемниками (нагрузкой) электрической энергии служат электрические двигатели, электронагревательные приборы и другие устройства, в которых электрическая энергия превращается в световую, тепловую, механическую и другие виды. Под элементами в теории электрических цепей подразумеваются обычно не физически существующие составные части электротехнических устройств, а их идеализированные модели, которым теоретически приписываются определенные электрические и магнитные свойства, так что они в совокупности приближенно отображают явления, происходящие в реальных устройствах. В электрических цепях различают активные и пассивные элементы. Активные элементы – это источники электрической энергии. Различают источники напряжения и источники тока. Пассивные элементы – это сопротивления, индуктивности, емкости. По наличию данных элементов различают соответственно активные и пассивные цепи. 2. Источники электрической энергии и их взаимное преобразование. Распределение потенциала вдоль участка ветви. Потенциальная диаграмма.
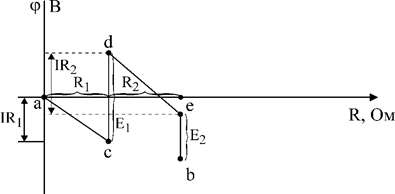
Рассмотрим участок электрической цепи (рис. 16)
Рис. 16.
Участок ветви, содержащий один или несколько источников энергии, является активным. Положительные направления тока и напряжения указаны стрелкой. Определим потенциалы точек c, d, e, b, предположив, что известен потенциал точки a-ja. Для правильного выбора знаков следует помнить, что: 1) ток в сопротивлении всегда направлен от более высокого потенциала к более низкому, т.е. потенциал падает по направлению тока. 2) э.д.с., направленная от точки «с» к точке «d», повышает потенциал последней на величину E. 3) напряжение U=Uac положительно, когда потенциал точки а выше, чем потенциал точки с. При обозначении напряжения (разности потенциалов) на схемах посредством стрелки она ставится в направлении от точки высшего потенциала к точке низшего потенциала. На рис. 16 ток протекает от точки «а» к точке «с», значит потенциал jс будет меньше ja на величину падения напряжения на сопротивлении R1, которое по закону Ома равно IR1: jс = ja - IR1 На участке cd э.д.с. E1 действует в сторону повышения потенциала, следовательно: jd = jс + E1 = ja - IR1+ E1 Потенциал точки «e» меньше потенциала точки «d» на величину падения напряжения на сопротивлении R2: je = jd – IR2 = ja - IR1+ E1– IR2 На участке e в э.д.с. E2 действует таким образом, что потенциал точки «b» меньше потенциала точки «e» на величину E2: jb = je – E2 = ja - IR1+ E1– IR2 – E2 = ja – I(R1+R2) + E1-E2 (15) Чтобы наглядно оценить распределение потенциала вдоль участка цепи, полезно построить потенциальную диаграмму, которая представляет график изменения потенциала вдоль участка цепи или замкнутого контура. По оси абсцисс графика откладываются потенциалы точек, а по оси ординат – сопротивления отдельных участков цепи. Для участка цепи рис. 16 распределение потенциала построено на рис. 17.
Рис. 16. Потенциальная диаграмма участка цепи.
Потенциальная диаграмма рис. 16 построена, начиная с точки a, которая условно принята за начало отсчета. Потенциал ja принят равным нулю. Точка цепи, потенциал которой условно принимается равным нулю, называется базисной. Если в условии задачи не оговорено, какая точка является базисной, то можно потенциал любой точки условно приравнивать к нулю. Тогда потенциалы всех остальных точек будут определяться относительно выбранного базиса. Обобщенный закон Ома. Закон Ома выражаемый формулой Определим зависимость между током, напряжением и э.д.с. на активном участке (рис. 16). Из формулы 15 следует: ja -jb=I(R1+R2)- E1+E2 (16) На положительное напряжение на участке a – b Uab=ja -jb Следовательно, Uab= I(R1+R2)- E1+E2 (17)
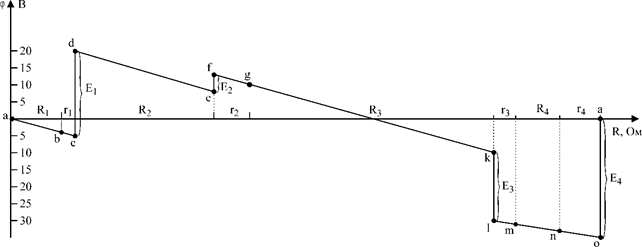
Формула (18) выражает обобщенный закон Ома, или закон Ома для участка, содержащего э.д.с. Из формулы видно, что если ток, напряжение и э.д.с. совпадают по направлению, то в выражение закона Ома они входят с одинаковыми знаками. Если э.д.с. действует в сторону, противоположную положительному направлению тока, то в выражении ставится знак «-». Закон Ома применяется для участка ветви и для одноконтурной замкнутой схемы. Пример № 1. Построения потенциальной диаграммы: Построить потенциальную диаграмму для одноконтурной схемы:
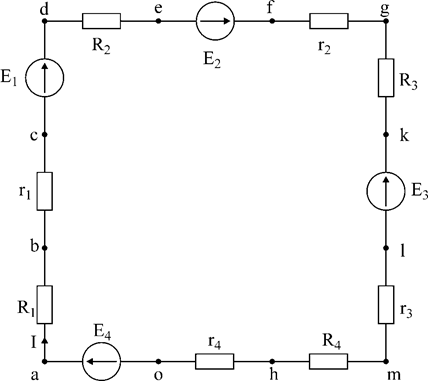
E1=25В; E2=5В; E3=20В; E4=35В, R1=8 Ом; R2=24 Ом; R3=40 Ом; R4=4 Ом, r1=2 Ом; r2=6 Ом; r3=2 Ом; r4=4 Ом. Решение: 1. перерисуем заданный контур, вынося внутренние сопротивления э.д.с. (r1- r4) за их пределы; обозначим точки контура.
Рис.2
2. Выберем положительное направление тока I, определим его значение используя обобщенный закон Ома:
3. За базисную точку примем точку a. Найдем потенциалы остальных точек: jb = ja – IR1 = - 4В je = jd – IR2 = 8В jc = jb – Ir1 = - 5В jf = je + E2 = 13В jd = jc + E1 = 20В jq = jf – Ir2 = 10В
jk = jq – IR3 = - 10В jn = jm – IR4 = - 33В je = jk – E3 = - 30В jo = jn – Ir4 = - 35В jm = je – Ir3 = - 31В ja = jo + E4 = 0
4. В системе координат строим потенциальную диаграмму:
1. Метод контурных токов. Метод контурных токов.
Метод контурных токов – один из основных и широко применяемых на практике методов. Он заключается в определении по второму закону Кирхгофа контурных токов. Для каждого контура цепи задают ток, который остается неизменным. В цепи протекает столько контурных токов, сколько независимых контуров в ней содержится. Направление контурного тока выбирают произвольно. Контурные токи, проходя через узел, остаются непрерывными. Следовательно, первый закон Кирхгофа выполняется автоматически. Уравнения с контурными токами записываются только для второго закона Кирхгофа. Число уравнений, составленных по методу контурных токов, меньше чем по методу законов Кирхгофа.
Рис.28. Иллюстрация к методу контурных токов.
На рис.28 показана цепь с двумя независимыми контурами, следовательно, и с двумя контурными токами I11 и I22. Токи в ветвях I1 и I2 равны контурным токам: I1=I11, I2=I22 Ток I3 равен сумме этих двух контурных токов: I3=I11+I22 По второму закону Кирхгофа для первого контура цепи: I1r1+I3r3=E1-E3 Или: I11r1+(I11+I22)r3=E1-E3; I11 (r1+r2)+I22r3=E1-E3 Обозначим r1+r2=r11 r3=r12; E1-E3 Тогда: I11r11+I2r12=E11 r11 – сумма всех сопротивлений, входящих в контур I, называется собственным сопротивлением контура. r12 – сопротивление ветви, общей для контура I и II; E11=E1-E2 – алгебраическая сумма всех э.д.с., содержащихся в первом контуре; со знаком «-» берется э.д.с., действующая навстречу контурному току рассматриваемого контура. E11 называется контурной э.д.с. Аналогично для второго контура рис.28. I11r21+I22r22=E22, где r21=r3; r22=r2+r3; E22=E2-E3 Уравнения, составленные по методу контурных токов, всегда записывают в виде системы. Для схемы рис.28:
В результате решения системы находят контурные токи, а затем токи ветвей. Если заданная электрическая цепь содержит n независимых контуров, то на основании второго закона Кирхгофа получается n контурных уравнений:
Собственные сопротивления rii входят в уравнения (29) со знаком «+», поскольку обход контура принимается совпадающим с положительным направлением контурного тока Iii. Общие сопротивления rik войдут в уравнения со знаком «-», когда токи Ii и Ik направлены в них встречно. Число уравнений, составляемых по методу контурных токов, определяется по формуле: Nур=Nb-Ny+1-Nи.т. где Nb – число ветвей электрической цепи; Ny – число узлов; Nи.т. – число идеальных источников тока.
Пример. Решим пример, используя метод контурных токов. (Для схемы рис.1 составить уравнения по законам Кирхгофа и определить неизвестные точки.) Дано: I1 = 20мA; I2 = 10мA R1 = 5kОм, R3 = 4kОм, R4 = 6kОм, R5 = 2kОм, R6 = 4kОм.
Цепь содержит три контура, через которые протекают контурные токи. При наличии источников тока надо так направлять контурные токи, чтобы они протекали через данные источники. Но через один источник тока не может протекать два контурных тока. На рис.1 обозначены положительные направления контурных токов. Очевидно, что I11=J1; I22=-J2 Контурный ток I33 – неизвестен, для него составляем уравнение: I33 (R3+R4+R5+R6)-I11 (R3+R4)+I22 (R5+R3)=0 В правой части уравнения стоит «0», т.к. отсутствует контурная э.д.с. В результате решения определяем I33=16,25 мА Итак: I1=I11=20мА; I3=I11-I22-I33=20-(-10)-16,25=13,75мА. I4=-I11+I33=-20+16,25=-3,75мА; I5=I22+I33=-10+16,25=6,25мА; I6=I33=16,25мА. 4. Применение законов Кирхгофа для расчета электрических цепей. 1 закон: алгебраическая сумма токов в узле равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:
2 закон: алгебраическая сумма падений напряжений в замкнутом контуре равна алгебраической сумме ЭДС этого контура.
8. Метод наложения. Входные и взаимные проводимости и сопротивления. Метод наложения основан на принципе наложения: ток в любой ветви электрической цепи от действия нескольких источников равен алгебраической сумме токов от действия каждого источника в отдельности. Входные и взаимные проводимости. Решение системы уравнений по законам Кирхгофа записывается в виде
Где коэффициенты g11,g22… называются входными проводимостями, а g12, g13… наз-ся взаимными проводимостями. Отношение контурного тока к ЭДС, действующей в том же контуре, при отсутствии независимых источников во всех остальных контурах называется входной проводимостью. Отношение контурного тока к ЭДС, действующей в другом контуре, при отсутствии независимых источников во всех остальных контурах называется передаточной (взаимной) проводимостью. Отношение напряжения в узле к току, заданному в том же узле, при отсутствии в схеме других независимых источников называется входным сопротивлением эл-кой цепи. Отношение напряжения в узле к току, заданному в другом узле, при отсутствии в схеме других источников называется передаточным (взаимным) сопротивлением узлов.
8. Метод узловых потенциалов (напряжений). Метод узловых напряжений заключается в том, что на основании первого закона Кирхгофа определяются потенциалы в узлах эл-кой цепи относительно базисного узла. Эти разности потенциалов называются узловыми напряжениями. Узловое напряжение- это напряжение в данном узле относительно базисного. Напряжение на какой-либо ветви равно разности узловых напряжений; произведение же этого напряжения на комплексную проводимость данной ветви равно току в этой ветви. Т.о., зная узловые напряжения в электрической цепи, можно найти токи в ветвях. Если принять потенциал базисного узла равным нулю, то напряжение между остальными узлами и базисным узлом будут равны также потенциалам этих узлов. Поэтому данный метод называется также методом узловых потенциалов. Собственная проводимость равняется сумме проводимостей ветвей сходящихся в данном узле. Величина положительная. 9.Применение метода узловых потенциалов при наличии в цепи идеальных источников эдс. За базисный принимается один из узлов между которыми находится идеальный источник ЭДС. Дано: Найти токи МУН. Nур =1;
-
В ветви с идеальным источником ток находится по первому закону Кирхгофа:
Дано: Найти токи МУН. Nур =1;
11)Метод преобразования Суть метода преобразований состоит в упрощении цепи и, как следствие, ее расчета. Последовательное соединение: 1)Преобразуем схему к простой (склеиваем все r и Е) 2)Треугольники преобразуем в звёзды 3)Находим ток в ветви 4)Раскрываем ветвь и считаем всё по току который нашли
Ток протекает везде одинаковый. Напряжение равно сумме всех напряжений. При параллельном соединении напряжение везде одинаковое. G0=1/R1 [см] – проводимость величина обратная сопротивлению.(сименс)
12) Преобразование треугольников в эквивалентную звезду-называется такая замена части цепи, соединенной по схеме треугольником цепью соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи сохраняются неизменной.

13)Эквивалентные преобразования активных соединений звездой и треугольником. Преобразование треугольников в эквивалентную звезду-называется такая замена части цепи, соединенной по схеме треугольником цепью соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи сохраняются неизменной.
Преобразуем ЭДС в источник тока по формулам I=E/rвн, g=1/rвн
14)Метод основан на методе наложения и используется в том случае, если схема содержит один источник. В этом методе произвольно задается ток самой дальней ветви от источника. По закону Ома и законам Кирхгофа определяют расчетные значения ЭДС источника. Вычисляя отношение расчетного значения ЭДС к заданному значению, получают коэффициент пропорциональности: 15)Баланс мощностей в цепи постоянного тока. Из закона сохранения энергии следует, что вся мощность поступающая в цепь от источников энергии в любой момент времени равна всей мощности потребляемой приемниками данной цепи.
Т.к. ток входит в выражение в квадрате, то независимо от его направления мощность потребителя всегда положительна. Мощность источника бывает как положительной так и отрицательной. РЕ=IE, где I – ток ветви с источником:
Мощность источника тока определяется по формуле: PI=IU, где I- значение тока источника, U–напряжение на его зажимах. Если ЭДС и ток в ветви в которой он находится совпадают по направлению, то мощность источника ЭДС входит в выражение баланса мощностей со знаком «+», если не совпадает то «-». Если ток Iи напряжение Uдействуют так, как показано на рисунке, то мощность в источнике тока положительная в противном случае отрицательная. Одноименные зажимы При анализе цепей с взаимной индуктивностью возникает задача определить, каким образом (согласно или встречно) по отношению к выбранным условным положительным направлениям токов включены рассматриваемые индуктивные катушки и в соответствие с этим какой знак (плюс или минус) необходимо использовать в выражениях (1), (2) (1) Если конструкции индуктивных катушек, в частности направления их намотки, известны, а направления токов заданы, то для выбора знака достаточно, воспользовавшись правилом буравчика (правоходового винта), определить направления магнитных потоков самоиндукции каждой из катушек. Например, применяя правило буравчика, устанавливаем, что у катушек, изображенных на рис. 3:
При вычерчивании принципиальных электрических схем цепей с взаимной индуктивностью индуктивные катушки изображают с помощью условных графических обозначений, которые не отражают особенностей их конструкции. Для выяснения, является ли данное включение катушек согласным или встречным, вводят понятие одноимённых зажимов связанных индуктивных Рис.3 катушек.
Одноименными зажимами двух связанных индуктивных катушек называется пара зажимов, выбранных таким образом при одинаковых относительно этих зажимов направлениях токов катушек магнитные потоки самоиндукции и взаимоиндукции в каждой из них суммируются. Одноименные зажимы индуктивных катушек помечают одинаковыми значками (буквами, точками, звездочками, треугольниками и т. п.), проставляемыми в непосредственной близости к соответствующим зажимам. Вторую пару одноименных зажимов катушек специально не обозначают (рис. 10.2). Когда общим магнитным потоком связано не две, а большее количество индуктивностей, одноимённые зажимы каждой из пар обозначают с помощью различных значков.
Итак, если токи связанных индуктивностей одинаково ориентированы относительно одноименных зажимов, то такое включение является согласным и в выражениях (1):
следует использовать знак плюс, в противном случае, включение является встречным и необходимо использовать знак минус (величина М при этом считается положительной). Например, индуктивности L1 и L2 на рис. 10.2 включены согласно, а индуктивности L2 и L3, L1 и L3 - встречно.
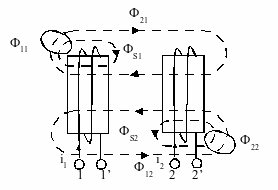
Воздушный трансформатор. Трансформатор служит для преобразования перекрёстного напряжения, когда нужно изменить его амплитуду, либо осуществить передачу электрической энергии между контурами лишённых гальванических элементов. Трансформатор представляет собой две или более связанных катушек (обмотки) которые могут быть помещены на один общий феромагнитный сердечник, или он может отсутствовать. В последнем случае трансформатор называется воздушным. Рассмотрим простейший воздушный трансформатор состоящий из двух обмотак.
Обмотка трансформатора подключённая к источнику переменного напряжения называется первичной, вторичная та, к которой подключена нагрузка ZH, представлена индуктивностью L2и сопротивлением R. Характеризуется индуктивностью М. Запишем 2-ой закон Кирхгофа для первичной и вторичной обмотки:
Элементы электрических цепей. Электрической цепью называется совокупность устройств, предназначенных для прохождения электрического тока. Электромагнитные процессы в электрических цепях описываются при помощи понятий «ток» и «напряжение». В общем случае электрическая цепь состоит из источников и приемников электрической энергии и промежуточных звеньев, связывающих источники с приемниками. Источники электрической энергии – гальванические элементы, аккумуляторы, термоэлементы, генераторы и другие устройства, в которых происходит процесс преобразования химической, тепловой, механической или другого вида энергии в электричес
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 429; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.013 с.) |


 , определяет зависимость между током и напряжением на пассивном участке электрической цепи.
, определяет зависимость между током и напряжением на пассивном участке электрической цепи. (18)
(18)
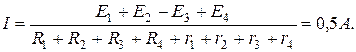


 (29)
(29) Если в цепи отсутствуют источники тока, число уравнений равно числу контурных токов и, соответственно, числу независимых контуров рассматриваемой электрической цепи.
Если в цепи отсутствуют источники тока, число уравнений равно числу контурных токов и, соответственно, числу независимых контуров рассматриваемой электрической цепи.
 .. 2 закон не записывается для контуров содержащих источники тока. Напряжение и ЭДС совпадающие с направлением обхода контура записываем со знаком (+), несовпадающие со знаком (-)
.. 2 закон не записывается для контуров содержащих источники тока. Напряжение и ЭДС совпадающие с направлением обхода контура записываем со знаком (+), несовпадающие со знаком (-) 


 =
=  =
= 
 -?
-? =
= 
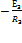
 ;
; ;
;

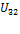 =-
=- 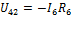 .
.



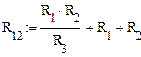





 .
.
 – мощность потребителей которыми в цепи постоянного тока являются резисторы.
– мощность потребителей которыми в цепи постоянного тока являются резисторы. (2)
(2)  .
. , направления магнитных потоков самоиндукции и взаимоиндукции у каждой из катушек одинаковы.
, направления магнитных потоков самоиндукции и взаимоиндукции у каждой из катушек одинаковы.
 (1)
(1)

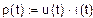


 Активная
P=UIcos(a)=I2r
Реактивная
Q=UIsin(a)= I2X
Полная
Рассмотрим мощности отдельных участков цепи с последовательным соединением R, L, C (рис. 2.15), для чего допустим, что к ней приложено напряжение
Активная
P=UIcos(a)=I2r
Реактивная
Q=UIsin(a)= I2X
Полная
Рассмотрим мощности отдельных участков цепи с последовательным соединением R, L, C (рис. 2.15), для чего допустим, что к ней приложено напряжение  и протекает ток
и протекает ток  .
Мощность в активном сопротивлении
.
Мощность в активном сопротивлении
 .
Учитывая RI = UR, а также равенство UR = Ucosφ, полученное из треугольника напряжений, будем иметь
.
Учитывая RI = UR, а также равенство UR = Ucosφ, полученное из треугольника напряжений, будем иметь
 .
.
 Рис. 2.15. Схема последовательной цепи
Из этого выражения видно:
1) мгновенная мощность в активном сопротивлении всегда положительна (т.е. всегда потребляется);
2) мгновенная мощность колеблется с двойной частотой около своего среднего значения, равного U I cos φ.
Кривая изменения мощности на активном сопротивлении показана на рис. 2.16.
Рис. 2.15. Схема последовательной цепи
Из этого выражения видно:
1) мгновенная мощность в активном сопротивлении всегда положительна (т.е. всегда потребляется);
2) мгновенная мощность колеблется с двойной частотой около своего среднего значения, равного U I cos φ.
Кривая изменения мощности на активном сопротивлении показана на рис. 2.16.
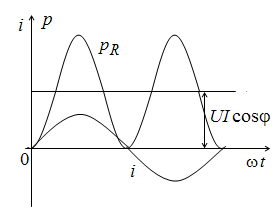 Рис. 2.16. Мгновенная мощность на активном сопротивлении
Мощность в индуктивности
Рис. 2.16. Мгновенная мощность на активном сопротивлении
Мощность в индуктивности
 .
Но
.
Но 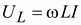 , следовательно,
, следовательно,  . Кривые тока и мощности показаны на рис. 2.17.
Из полученного выражения видно, что мгновенная мощность в индуктивности колеблется с двойной частотой около своего нулевого значения. Следовательно, каждые четверть периода энергия поступает в магнитное поле катушки, чтобы в последующие четверть периода вернуться полностью в источник питания, т.е. идеальная катушка индуктивности энергии не потребляет.
. Кривые тока и мощности показаны на рис. 2.17.
Из полученного выражения видно, что мгновенная мощность в индуктивности колеблется с двойной частотой около своего нулевого значения. Следовательно, каждые четверть периода энергия поступает в магнитное поле катушки, чтобы в последующие четверть периода вернуться полностью в источник питания, т.е. идеальная катушка индуктивности энергии не потребляет.
 Рис. 2.17. Кривые тока и мощности на индуктивности
Мощность в емкости
Рис. 2.17. Кривые тока и мощности на индуктивности
Мощность в емкости

 .
Кривые тока и мощности показаны на рис. 2.18.
.
Кривые тока и мощности показаны на рис. 2.18.
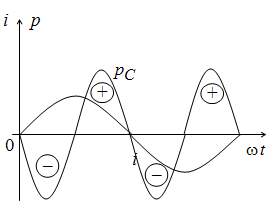 Рис. 2.18. Кривые тока и мощности на емкости
Эти выражения показывают, что в конденсаторе емкостью С энергия не потребляется. Так же, как и в индуктивности, она колеблется около нулевого значения с двойной частотой, поступая от источника и возвращаясь к нему. Следует отметить, что мощности в индуктивности и в емкости колеблются в противофазе. Это говорит о том, что магнитное и электрическое поле способны обмениваться запасами энергии друг с другом.
В соответствии с этим суммарная мгновенная мощность, накапливаемая в индуктивности и емкости, будет равна
Рис. 2.18. Кривые тока и мощности на емкости
Эти выражения показывают, что в конденсаторе емкостью С энергия не потребляется. Так же, как и в индуктивности, она колеблется около нулевого значения с двойной частотой, поступая от источника и возвращаясь к нему. Следует отметить, что мощности в индуктивности и в емкости колеблются в противофазе. Это говорит о том, что магнитное и электрическое поле способны обмениваться запасами энергии друг с другом.
В соответствии с этим суммарная мгновенная мощность, накапливаемая в индуктивности и емкости, будет равна
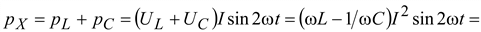
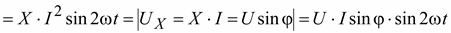 .
Этой мощностью, называемой мгновенной реактивной мощностью, реактивные элементы обмениваются не между собой, а с источником питания.
При
.
Этой мощностью, называемой мгновенной реактивной мощностью, реактивные элементы обмениваются не между собой, а с источником питания.
При  , т.е. в режиме резонанса напряжений, эта реактивная мощность равна нулю и катушка и конденсатор обмениваются энергией только между собой, на получая ничего от источника и не возвращая в него.
Определим мгновенную полную мощность.
Если к участку цепи приложено напряжение u = Um×sin(ω×t + φ) и по нему протекает ток i = Im×sin ω×t, то мгновенная мощность, поступающая в цепь, будет равна
, т.е. в режиме резонанса напряжений, эта реактивная мощность равна нулю и катушка и конденсатор обмениваются энергией только между собой, на получая ничего от источника и не возвращая в него.
Определим мгновенную полную мощность.
Если к участку цепи приложено напряжение u = Um×sin(ω×t + φ) и по нему протекает ток i = Im×sin ω×t, то мгновенная мощность, поступающая в цепь, будет равна
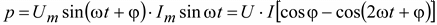 . (2.34)
Она состоит из двух слагающих: постоянной величины
. (2.34)
Она состоит из двух слагающих: постоянной величины 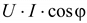 , равной постоянной составляющей мгновенной мощности активного сопротивления, и гармонической, имеющей двойную частоту.
Средняя мощность
, равной постоянной составляющей мгновенной мощности активного сопротивления, и гармонической, имеющей двойную частоту.
Средняя мощность
 .
Эта мощность выделяется в приемниках электрической энергии. Множитель cos φ носит наименование коэффициента мощности.
.
Эта мощность выделяется в приемниках электрической энергии. Множитель cos φ носит наименование коэффициента мощности.
 ;
;
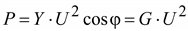 .
Согласно (2.34) мгновенная мощность колеблется с двойной частотой 2ω относительно средней мощности P = U I cos φ.
На рис. 2.19 показаны кривые изменения во времени тока, напряжения и мощности цепи.
Когда ток и напряжение имеют одинаковый знак, мгновенная мощность положительна, и энергия поступает от источника к приемнику, где преобразуется в тепло (на активном сопротивлении) и запасается в магнитном поле катушки индуктивности или в электрическом поле конденсатора. Когда ток и напряжение имеют разные знаки, мгновенная мощность отрицательна, и энергия возвращается от приемника к источнику.
На практике пользуются понятиями активной, реактивной и полной мощности.
.
Согласно (2.34) мгновенная мощность колеблется с двойной частотой 2ω относительно средней мощности P = U I cos φ.
На рис. 2.19 показаны кривые изменения во времени тока, напряжения и мощности цепи.
Когда ток и напряжение имеют одинаковый знак, мгновенная мощность положительна, и энергия поступает от источника к приемнику, где преобразуется в тепло (на активном сопротивлении) и запасается в магнитном поле катушки индуктивности или в электрическом поле конденсатора. Когда ток и напряжение имеют разные знаки, мгновенная мощность отрицательна, и энергия возвращается от приемника к источнику.
На практике пользуются понятиями активной, реактивной и полной мощности.
 Рис. 2.19. Кривые изменения тока, напряжения и мощности
Под активной мощностью понимают среднее значение полной мгновенной мощности за период
P = U I cos φ.
Активная мощность никогда не бывает отрицательной, так как ею характеризуется потребление энергии цепью. Единицей измерения активной мощности принят ватт (Вт).
Реактивная мощность (Q) характеризует ту часть энергии, которой цепь обменивается с источником без потребления. Ее величина определяется амплитудным значением мгновенной реактивной мощности, выражение которой было ранее получено в виде U I sinφ sin 2ωt. Следовательно,
Q = U I sin φ.
Реактивную мощность принято измерять в вольт-амперах реактивных (ВАр). Она положительна при отстающем токе (когда φ > 0) и отрицательна при опережающем (когда φ < 0).
Полезная работа, совершаемая элементами цепи, характеризуется активной мощностью P. Однако эта мощность зависит от угла сдвига фаз φ, значение которого может меняться в зависимости от режима работы цепи. Следовательно, активная мощность не может быть той расчетной величиной, на которую можно приводить расчет электрических машин, аппаратов и других устройств. Поэтому их характеризуют полной мощностью
S = U×I,
являющейся произведением действующих значений тока и напряжения. Полная мощность равна наибольшему значению активной мощности, которую можно получить при заданных токе и напряжении. Единицей измерения полной мощности принят вольт-ампер (ВА).
Активная, реактивная и полная мощности связаны между собой соотношениями прямоугольного треугольника, называемого треугольником мощностей (рис. 2.20):
Рис. 2.19. Кривые изменения тока, напряжения и мощности
Под активной мощностью понимают среднее значение полной мгновенной мощности за период
P = U I cos φ.
Активная мощность никогда не бывает отрицательной, так как ею характеризуется потребление энергии цепью. Единицей измерения активной мощности принят ватт (Вт).
Реактивная мощность (Q) характеризует ту часть энергии, которой цепь обменивается с источником без потребления. Ее величина определяется амплитудным значением мгновенной реактивной мощности, выражение которой было ранее получено в виде U I sinφ sin 2ωt. Следовательно,
Q = U I sin φ.
Реактивную мощность принято измерять в вольт-амперах реактивных (ВАр). Она положительна при отстающем токе (когда φ > 0) и отрицательна при опережающем (когда φ < 0).
Полезная работа, совершаемая элементами цепи, характеризуется активной мощностью P. Однако эта мощность зависит от угла сдвига фаз φ, значение которого может меняться в зависимости от режима работы цепи. Следовательно, активная мощность не может быть той расчетной величиной, на которую можно приводить расчет электрических машин, аппаратов и других устройств. Поэтому их характеризуют полной мощностью
S = U×I,
являющейся произведением действующих значений тока и напряжения. Полная мощность равна наибольшему значению активной мощности, которую можно получить при заданных токе и напряжении. Единицей измерения полной мощности принят вольт-ампер (ВА).
Активная, реактивная и полная мощности связаны между собой соотношениями прямоугольного треугольника, называемого треугольником мощностей (рис. 2.20):
 ;
;
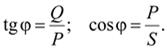
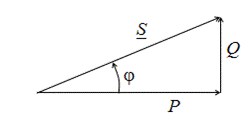 Рис. 2.20. Треугольник мощностей
Активная мощность определяет ту работу, которая в среднем совершается (передается) в электрической цепи. Полная и реактивная мощности не определяют ни совершаемой работы, ни передаваемой энергии. Полная мощность, часто называемая кажущейся, является пределом, которого следует добиваться в целях повышения КПД. Реактивная мощность является условной величиной, характеризующей энергию электрических и магнитных полей, имеющихся в цепи.
Запишем мощность в комплексной форме
Символическое представление действующих значений тока I и напряжения U позволяет легко и просто найти активную реактивную и полную мощности. Для этого необходимо взять произведение комплексного напряжения U и комплекса
Рис. 2.20. Треугольник мощностей
Активная мощность определяет ту работу, которая в среднем совершается (передается) в электрической цепи. Полная и реактивная мощности не определяют ни совершаемой работы, ни передаваемой энергии. Полная мощность, часто называемая кажущейся, является пределом, которого следует добиваться в целях повышения КПД. Реактивная мощность является условной величиной, характеризующей энергию электрических и магнитных полей, имеющихся в цепи.
Запишем мощность в комплексной форме
Символическое представление действующих значений тока I и напряжения U позволяет легко и просто найти активную реактивную и полную мощности. Для этого необходимо взять произведение комплексного напряжения U и комплекса  , сопряженного с комплексным током I
, сопряженного с комплексным током I



 .
Из этого выражения видно, что вещественная часть комплексной мощности равна активной мощности, мнимая часть – реактивной. Модуль комплексной мощности S равен полной мощности S.
.
Из этого выражения видно, что вещественная часть комплексной мощности равна активной мощности, мнимая часть – реактивной. Модуль комплексной мощности S равен полной мощности S.
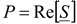 ;
;  ;
;
 ;
;
 .
.

 ; то же для Zn
; то же для Zn 
 Первое условие:
Первое условие:  Тогда получим:
Тогда получим:
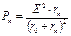


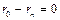 Получили второе условие:
Получили второе условие:  Максимальная мощность, которая выделится на нагрузке:
Максимальная мощность, которая выделится на нагрузке:
 Производимая генераторами мощность равна потребляемой мощности. Средняя мощность, генерируемая источником, равна средней мощности, потребляемой всеми потребителями. Сумма отдаваемых реактивных мощностей также равна сумме потребляемых реактивных мощностей:
Производимая генераторами мощность равна потребляемой мощности. Средняя мощность, генерируемая источником, равна средней мощности, потребляемой всеми потребителями. Сумма отдаваемых реактивных мощностей также равна сумме потребляемых реактивных мощностей:
 или
или  и
и  .
Для определения величины и характера сопротивления Z = R + jX, обеспечивающего максимум передаваемой активной мощности, представим источник электрической энергии как последовательное соединение источника напряжения E = E∠0 и внутреннего сопротивления Zв = Rв + jXв (рис. 2.21).
Мощность приемника будет равна
.
Для определения величины и характера сопротивления Z = R + jX, обеспечивающего максимум передаваемой активной мощности, представим источник электрической энергии как последовательное соединение источника напряжения E = E∠0 и внутреннего сопротивления Zв = Rв + jXв (рис. 2.21).
Мощность приемника будет равна  .
При любом активном сопротивлении приемника R мощность будет максимальна, если суммарное реактивное сопротивление X + Xв = 0, т.е. при X = – Xв. В этом случае
.
При любом активном сопротивлении приемника R мощность будет максимальна, если суммарное реактивное сопротивление X + Xв = 0, т.е. при X = – Xв. В этом случае 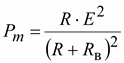 .
.
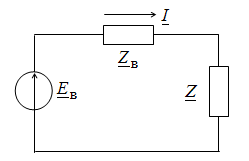 Рис. 2.21. Схема электропередачи
Взяв производную по R и приравняв ее нулю, находим, что Pm будет иметь наибольшее значение при R = Rв.
Таким образом, приемник получает от источника наибольшую активную мощность тогда, когда его комплексное сопротивление оказывается сопряженным с внутренним сопротивлением источника
Рис. 2.21. Схема электропередачи
Взяв производную по R и приравняв ее нулю, находим, что Pm будет иметь наибольшее значение при R = Rв.
Таким образом, приемник получает от источника наибольшую активную мощность тогда, когда его комплексное сопротивление оказывается сопряженным с внутренним сопротивлением источника  .
При этом условии
.
При этом условии  .КПД в этом случае будет равно
.КПД в этом случае будет равно
 . энергетических установках такой режим передачи максимальной мощности невыгоден из-за низкого КПД.
. энергетических установках такой режим передачи максимальной мощности невыгоден из-за низкого КПД.







