
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синусоидальный ток в индуктивности.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Выделим индуктивный элемент (рис1). Положительные направления тока i через него, ЭДС самоиндукции eL и напряжение на нем uabуказаны на рис.1.
Если Следовательно, Произведение ωL обозначается XL, индуктивным сопротивлением и измеряется в Омах (Ом): Таким образом, индуктивный элемент (индуктивная катушка, у которой R=0) при синусоидальном токе обладает сопротивлением, модуль которого 21. Согласно 2-ому закону Кирхгофа:
Z- сопротивление комплексное,
Х – реактивное сопротивление (комплексное) м.б. положительным и отрицательным в зависимости от того какое из слагаемых больше R – активное сопротивление, Zm = |Z|; Первый закон Кирхгофа в комплексной форме:
Второй закон Кирхгофа в комплексном виде:
К.ч. можно представить в виде вектора на комплексной плоскости. Диаграмма отражающая совокупность векторов токов и напряжений с учетом их фаз по 1-ому и 2-ому законам Кирхгофа на комплексной плоскости называется векторной диаграммой В цепи с индуктивностью ток наводит в катушке индуктивности ЭДС самоиндукции, которая уравновешивается напряжением приложенным к катушке.
В цепи с индуктивностью ток в катушке отстает от на пряжения на pi/2Физический смысл индуктивного сопротивления заключается в припятствовании прохождению тока ЭДС самоиндукции при прохождении по катушке индуктивности переменного тока и направленно на встречу приложенному к катушке напряжению При Конденсатор
В цепи с емкостью ток опережает напряжение по фазе на 90 градусов. Физический смысл емкостного сопротивления заключается в припятствовании прохождению тока через конденсатор из-за наличия заряда на его обкладках.
При 22. Параллельное соединение
в- реактивная проводимость g- активная проводимость Y-комплексная полная проводимость 24.Произведение мгновенного зн-я, приложенного к цепи напряжения, и мгновенного значения проходящего по ней тока называется мгновенной мощностью. P(t)=U(t)i(t)
Используя формулу произведения синуса и формулы для расчета действ. значений
ð Мгновенная мощность имеет постоянную и переменную составляющую, изменяющуюся во времени с частотой. При При При
Для цепей синусоидального тока:
Измеряется в Ваттах Она характеризует энергию, которая передается от источника к нагрузке, где превращается в другие виды энергий. Множитель ( Произведения действительного напряжения и тока, а также синус угла сдвига между ними называется реактивной мощностью
Измеряется в варах Реактивная мощность характеризует энергию,которая периодически циркулирует между источником и нагрузкой. Произведение действительного тока и напряжения называется полной мощностью. S=UI Измеряется в вольт-амперах 25. Графоаналитический метод – это совокупность графического метода и метода пропорционального пересчета, который основан на линейности электрических цепей. Векторная диаграмма построенная для питающего направления в линейных цепях. В линейных цепях не изменяет своего вида и для другого значения питающего направления, изменяются только масштабы токов и напряжений.
Построенная таким образом диаграмма называется топографической диаграммой. Топографические диаграммы представляют собой диаграммы комплексных потенциалов Особенности построения: 1. Построение векторной диаграммы начинается из точки визуально более отдаленной от входных зажимов и соответствующей отрицательной полярности входного напряжения 2. Построение векторов напряжений ведется на встречу токам. 3. Вектор на топографической диаграмме направлен к точке высшего потенциала 4. Построение ведется строго в соответствии со структурой цепи. Каждой точке схемы соответствуюет определенная точка топографичесой диаграммы 23. Эквивалентные параметры сложной цепи переменного тока, рассматриваемой как двухполюсник Для любой сложной цепи с постоянными параметрами при синусоидальном напряжении на ее входных зажимах общий входной ток цепи будет также синусоидальным и в общем случае сдвинут по отношению к напряжению на угол φ.
Назовем эквивалентным полным сопротивлением всей цепи отношение действующих напряжения и тока на входе цепи: Оно может быть измерено с помощью вольтметра и амперметра. Эквивалентное активное сопротивление всей цепи определим как отношение активной мощности на зажимах цепи к квадрату действующего тока: Эквивалентное реактивное сопротивление всей цепи определим так, чтобы сохранилась связь причем знак «плюс» ставим, если φ > 0, и знак «минус», если φ < 0. Для определения знака угла φ нужно располагать фазометром, или можно, например, поступить следующим образом: включив последовательно с цепью катушку, имеющую индуктивное сопротивление, меньшее абсолютного значения Аналогично определим эквивалентные проводимости из соотношений: причем, так же как и для Установим связь между эквивалентными сопротивлениями и проводимостями и углом φ. Для активного сопротивления имеем: и из соотношения В последнем выражении при извлечении квадратного корня из Соответственно, для активной проводимости получим выражение и из соотношения Из полученных выражений имеем Учитывая соотношения (1.37) - (1.40), получаем связь между эквивалентными сопротивлениями и проводимостями:
Рис 1. φ > 0 и φ<0
Формально всегда можно разложить вектор напряжения на две составляющие: вдоль вектора тока и перпендикулярно ему. Эти составляющие, соответственно, будут равны
Аналогично можно разложить вектор тока на вдоль вектора напряжения и перпендикулярно ему. Эти составляющие (рис ------->) равны
Их иногда называют активной и реактивной составляющими тока, а образуемые ими и вектором Как составляющие треугольников сопротивлений, так и составляющие треугольников проводимостей не являются вращающимися векторами, так как Обратим внимание также на то, что разложение напряжения на активную и реактивную составляющие (рис.1) имеет физический смысл только для простой последовательной цепи, так как при этом активная составляющая равна падению напряжения на участке с сопротивлением Для параллельной цепи, а также для сложной цепи такое разложение является чисто формальным. Соответственно, разложение тока на активную и реактивную составляющие имеет физический смысл только для простой параллельной цепи, а в общем случае является формальным.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 706; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.40.102 (0.011 с.) |

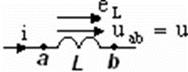 рис.1.
рис.1. , то
, то  Определим разность потенциалов между точками a и b. При перемещении от точки b к точке а идем встречно ЭДС eL, поэтому
Определим разность потенциалов между точками a и b. При перемещении от точки b к точке а идем встречно ЭДС eL, поэтому 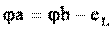 и
и 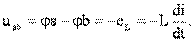 В дальнейшем напряжение на индуктивном элементе будем обозначать uL или, просто, u без индекса
В дальнейшем напряжение на индуктивном элементе будем обозначать uL или, просто, u без индекса 
 ;(1)
;(1)
 .
. прямо пропорционален частоте ω [см.(1)] – на рис.2 вектор напряжений
прямо пропорционален частоте ω [см.(1)] – на рис.2 вектор напряжений  опережает вектор тока I на 900. Комплекс ЭДС самоиндукции
опережает вектор тока I на 900. Комплекс ЭДС самоиндукции  находится в противофазе с комплексом напряжений
находится в противофазе с комплексом напряжений  . Графики мгновенных значений i, u, p изображены на рис.3.
. Графики мгновенных значений i, u, p изображены на рис.3.


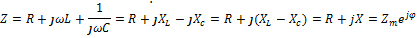
 - комплексное сопротивление индуктивности
- комплексное сопротивление индуктивности – комплексное сопротивление емкости
– комплексное сопротивление емкости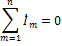
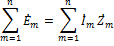

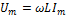

 =0 XL=0 (для постоянного тока)
=0 XL=0 (для постоянного тока)
 ,
,  , т.е. в установившемся режиме конденсатор не пропускает постоянный ток.
, т.е. в установившемся режиме конденсатор не пропускает постоянный ток.
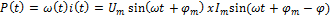
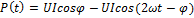
 мгновенная мощность изменяется по синусоидальному закону относительно прямой
мгновенная мощность изменяется по синусоидальному закону относительно прямой  с частотой вдвое больше частоты напряжения и тока и имеет как положительные так и отрицательные участки.
с частотой вдвое больше частоты напряжения и тока и имеет как положительные так и отрицательные участки. мгновенная мощность изменяющихся по гармоническому закону относительно прямой UI также с удвоенной частотой, принимает положительные значения. Между конденсатором и катушкой происходит взаимный обменэнергией без возврата ее к источнику.
мгновенная мощность изменяющихся по гармоническому закону относительно прямой UI также с удвоенной частотой, принимает положительные значения. Между конденсатором и катушкой происходит взаимный обменэнергией без возврата ее к источнику. мгновенная мощность изменяется по гармоническому закону относительно оси времени также с удвоенной частотой, в этом случае вся энергия, поступающая в цепь, возвращается в цепь. Среднее значение мгновенной мощности за период называется активной мощностью.
мгновенная мощность изменяется по гармоническому закону относительно оси времени также с удвоенной частотой, в этом случае вся энергия, поступающая в цепь, возвращается в цепь. Среднее значение мгновенной мощности за период называется активной мощностью.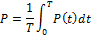

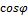 ) называется коэффициентом мощности.
) называется коэффициентом мощности.
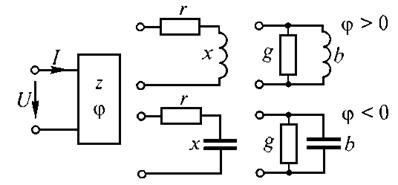 Рассматривая всю цепь в целом как двухполюсник и не интересуясь ее внутренним строением, можно характеризовать ее некоторыми эквивалентными параметрами. На рисунке эта двухполюсная цепь изображена в виде прямоугольника.
Рассматривая всю цепь в целом как двухполюсник и не интересуясь ее внутренним строением, можно характеризовать ее некоторыми эквивалентными параметрами. На рисунке эта двухполюсная цепь изображена в виде прямоугольника.

 которая имела место для рассмотренных выше простейших цепей, т.е.
которая имела место для рассмотренных выше простейших цепей, т.е.
 рассматриваемой цепи, повторно произвести измерение величин
рассматриваемой цепи, повторно произвести измерение величин  и вычислить
и вычислить  . Если при этом реактивное сопротивление увеличится, т.е.
. Если при этом реактивное сопротивление увеличится, т.е.  то это значит, что φ>0. В противном случае φ < 0.
то это значит, что φ>0. В противном случае φ < 0.


 , будем считать bЭ> 0 при φ > 0 и bЭ< 0 при φ < 0. В дальнейшем условимся опускать индекс «э».
, будем считать bЭ> 0 при φ > 0 и bЭ< 0 при φ < 0. В дальнейшем условимся опускать индекс «э». (1.37)
(1.37) для реактивного сопротивления получаем
для реактивного сопротивления получаем . (1.38)
. (1.38) взят знак «плюс», так как мы условились считать х > 0 при φ > 0.
взят знак «плюс», так как мы условились считать х > 0 при φ > 0. (1.39)
(1.39) для реактивной проводимости найдем
для реактивной проводимости найдем .(1.40)
.(1.40)

 Сказанное выше можно проиллюстрировать векторными диаграммами (рис1).
Сказанное выше можно проиллюстрировать векторными диаграммами (рис1).
 и
и  . Эти составляющие иногда называют активной и реактивной составляющими приложенного напряжения, а образуемые ими и вектором
. Эти составляющие иногда называют активной и реактивной составляющими приложенного напряжения, а образуемые ими и вектором  прямоугольные треугольники – треугольниками напряжения. Разделив все стороны этих треугольников на
прямоугольные треугольники – треугольниками напряжения. Разделив все стороны этих треугольников на  , получим треугольники сопротивлений, катетами которых являются эквивалентные активные и реактивные сопротивления, а гипотенузой – эквивалентное полное сопротивление.
, получим треугольники сопротивлений, катетами которых являются эквивалентные активные и реактивные сопротивления, а гипотенузой – эквивалентное полное сопротивление. и
и 
 прямоугольные треугольники – треугольниками тока. Разделив все стороны этих треугольников на U, получим треугольники проводимостей, катетами которых являются эквивалентные активные и реактивные проводимости, а гипотенузой – эквивалентная полная проводимость.
прямоугольные треугольники – треугольниками тока. Разделив все стороны этих треугольников на U, получим треугольники проводимостей, катетами которых являются эквивалентные активные и реактивные проводимости, а гипотенузой – эквивалентная полная проводимость. и у не изображают функций времени, как это имеет место для векторов
и у не изображают функций времени, как это имеет место для векторов  и реактивная составляющая равна падению напряжения на участке, содержащем конденсатор и катушку.
и реактивная составляющая равна падению напряжения на участке, содержащем конденсатор и катушку.


