
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт цепей с несинусоидальными периодическими э.д.с., напряжениями, токамиСодержание книги
Поиск на нашем сайте
Расчёт линейных электрических цепей несинусоидального тока распадается на три этапа: а) разложение несинусоидальных э.д.с. и токов источников на постоянную и синусоидальные составляющие (т.е. в тригонометрический ряд Фурье); Разложение периодических несинусоидальных кривых в ряд Фурье Периодическая функция где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд Фурье
Здесь
где Т – период несинусоидальной периодической функции. В выражении (13.1)
Свойства периодических кривых, обладающих симметрией:
Рисунок 13.2
а) кривые, симметричные относительно оси абсцисс. К данному типу относятся кривые, удовлетворяющие равенству
Рисунок 13.3 Рисунок 13.4 б) кривые, симметричные относительно оси ординат. К данному типу относятся кривые, для которых выполняется равенство в) кривые, симметричные относительно начала координат. К этому типу относятся кривые, удовлетворяющие равенству
б) применение принципа наложения и расчет токов и напряжений в цепи для каждой из составляющих в отдельности. При расчете цепи с постоянными составляющими э.д.с. и тока источника следует учитывать, что индуктивное сопротивление равно 0 и индуктивность в эквивалентной схеме заменяется короткозамкнутым участком, а ёмкостное равно в) совместное рассмотрение решений, полученных для каждой из составляющих. Причём суммируются только мгновенные значения составляющих токов и напряжений.
Тема 6: Четырехполюсники Общее положение 4-х-п – эл цепь, содержащая 2 пары зажимов (4 полюса) и предназначена для передачи эл энергии от генератора к нагрузке. Та пара зажимов, к к-ым подключается генератор, наз. входным Та пара зажимов, к к-ым подключается нагрузка, наз. выходным Классификация 4-х-п: Линейные и нелинейные. Линейные отличаются от нелинейных тем, что не содержат нелинейных эл-ов и поэтому х-ся линейной зав-стью напряжения и тока на выходных зажимах от напряжения и тока на входных зажимах Пассивный активный. Пассивные не содержат источников эл энергии, активные-содержат (завис-ые и незав-ые). Симметричные (перемена местами входных и выходных зажимов не изменяет напряжений и токов в цепи) несимметричные. Мостовые, лестничные (Г,Т,П – образные) Уравновешенные (горизонтальная ось симметрии) неуравновешенные Обратимые (передают энергию в обоих направлениях, т. обратимости: отношение напряжение на входе к току на выходе не меняется при перемене местами зажимов) необратимые Уравнение передачи четырехполюсника Ур-ия, связывающие токи и напряжения на входе и выходе 4-х-п, наз ур-ми передачи 4-х-п Ур-е передачи в А- параметрах:
Ур-е передачи в У- параметрах:
по размерности – проводимость Ур-е передачи в Z- параметрах:
по размерности – сопротивление Ур-е передачи в H- параметрах:
Ур-е передачи в F- параметрах:
Ур-е передачи в В- параметрах:
Параметры холостого хода и короткого замыкания четырехполюсника Параметрами холостого хода (ХХ) и короткого замыкания (КЗ) называются Входные сопротивления четырёхполюсника в режиме холостого хода на зажимах
При коротком замыкании зажимов
Параметры ХХ и КЗ удовлетворяют соотношению:
Характеристические параметры четырехполюсника
|
||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 217; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.197.120 (0.009 с.) |


 .
.
 - постоянная составляющая или нулевая гармоника;
- постоянная составляющая или нулевая гармоника; - первая (основная) гармоника, изменяющаяся с угловой частотой
- первая (основная) гармоника, изменяющаяся с угловой частотой 
 . Коэффициенты А0, аК и bK определяются по формулам
. Коэффициенты А0, аК и bK определяются по формулам ,
,  ,
,  .
.
 (рисунок 13. 2). В их разложении отсутствуют постоянная составляющая и четные гармоники, т.е.
(рисунок 13. 2). В их разложении отсутствуют постоянная составляющая и четные гармоники, т.е.  ;
;

 (рисунок 13.3). В их разложении отсутствуют синусные составляющие, т.е.
(рисунок 13.3). В их разложении отсутствуют синусные составляющие, т.е.  ;
; (рисунок 13.4). При разложении таких кривых отсутствуют постоянная и косинусные составляющие, т.е.
(рисунок 13.4). При разложении таких кривых отсутствуют постоянная и косинусные составляющие, т.е.  .
.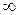 и ветвь с ёмкостью размыкается. При расчете цепи для каждой синусоидальной составляющей э.д.с. и тока источника можно пользоваться комплексным методом, но недопустимо сложение комплексных токов и напряжений различных синусоидальных составляющих. Необходимо учитывать, что индуктивное и емкостное сопротивления для различных частот неодинаковы, индуктивное сопротивление для k-й гармоники равно:
и ветвь с ёмкостью размыкается. При расчете цепи для каждой синусоидальной составляющей э.д.с. и тока источника можно пользоваться комплексным методом, но недопустимо сложение комплексных токов и напряжений различных синусоидальных составляющих. Необходимо учитывать, что индуктивное и емкостное сопротивления для различных частот неодинаковы, индуктивное сопротивление для k-й гармоники равно:  , а емкостное сопротивление для k-й гармоники равно:
, а емкостное сопротивление для k-й гармоники равно:  ;
;
 безразмерные,
безразмерные,  размерность сопротивления,
размерность сопротивления,  - размерность проводимости
- размерность проводимости


 - безразмерные,
- безразмерные,  - сопротивление, проводимость
- сопротивление, проводимость
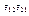 - безразмерные,
- безразмерные,  - проводимости и сопротивления
- проводимости и сопротивления
 и
и  при разомкнутых и замкнутых накоротко зажимах четырёхполюсника.
при разомкнутых и замкнутых накоротко зажимах четырёхполюсника. (ZH2=
(ZH2=  , I2=0) и
, I2=0) и 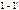 (ZH1=
(ZH1=  ,
, 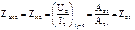 .
. ,
,  .
.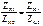 , т.е.только три параметра из четырёх независимы и их достаточно для составления уравнений передачи пассивных четырёхполюсников, из параметров ХХ и КЗ может быть получена любая система параметров-коэффициентов пассивных четырёхполюсников. Для симметричных четырёхполюсников А11=А22, ZX1=ZX2, ZK1=ZK2.
, т.е.только три параметра из четырёх независимы и их достаточно для составления уравнений передачи пассивных четырёхполюсников, из параметров ХХ и КЗ может быть получена любая система параметров-коэффициентов пассивных четырёхполюсников. Для симметричных четырёхполюсников А11=А22, ZX1=ZX2, ZK1=ZK2.


