
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы электрической цепи (активные, пассивные)Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Элементы электрической цепи (активные, пассивные) Эл. цепью наз. совокупность устройств, предназначенных для прохождения тока и описываемых с помощью понятий тока и напряжения Пассивные элементы. Резистивным сопротивлением наз. идеализированный элемент, обладающий только свойством необратимого рассеивания энергии.
Количественной характеристикой: Сопротивление R Ом, проводимость (G=1/R, См) Математическая модель, описывающая св-ва резистивного сопротивления, определяется з-ном Ома: напряжения от тока, наз. вольт-амперной х-кой (ВАХ). Если R постоянно, то ВАХ линейна, если R зав-ит от напряжения и тока, то ВАX нелинейное Мощность в резистивном сопротивлении: Индуктивным эл-ом наз. идеализированный эл-т эл. цепи, обладающий только св-вом накопления им энергии магнитного поля.
Математическая модель, описывающая св-ва индуктивного элемента определяется соотношением Количественная х-ка: индуктивность(положитеьлное). Если L=сonst, зав0ость ВАХ линейная, если зав-ит от тока и напряжения- нелинейная
емкостным эл-от наз. идеализированный эл-т эл цепи, обладающий только св-вом накапливать энергию эл поля.
Математическая модель, описывающая св-ва емкостного эл-та, опред-ся ВАХ: Количественная х-ка: емкость (С)(положительна) Если С=сonst, зав-ость ВАХ линейная, если зав-ит от тока и напряжения- нелинейная
Активные эл-ты: завис-ые и незав-ые источники эл энергии Независимым источником напряжения наз. идеализированный двухполюсный Эл-т, напряжение на зажимах к-ого не зав-ит от протекающего через него тока. Х-ся своим задающим напряжением Uг, или ЭДС ег ВАХ – прямая, параллельная оси токов Независимым источником тока наз идеализированный двухполюсный эл-т, ток к-ого не зав-ит от напряжения на его зажимах Х-ся своим заданный током iг ВАх- прямая, параллельная оси напряжения Зависимый источник - четырехполюсный эл-т с 2-мя парами зажимов- входных и выходных Зависимые источники: источник напряжения, управляемый напряжением; источник тока, управляемый напряжением; источник напряжения, управляемый током; источник тока, управляемый током. Законы Кирхгофа. Закон Ома 1-ый з-н Кирхгофа (з-н токов): алгебраическая сумма токов ветвей, сходящихся в одном узле эл цепи, равна нулю Число независимых ур-ий =nу-1 2-ой з-н Кирхгофа (з-н напряжений): алгебраическая сумма напряжений ветвей в любом контуре равна нулю 2-ой з-н Кирхгофа: (для падении янапряжений): алгебраическая сумма падений напряжений на Эл-ах в замкнутом контуре= алгебраической сумме ЭДС, действующих в данном контуре: Число Ур-ий = nв-nу+1-nит З-н Ома:
3. Преобразование эл схем Последовательное соединение эл-ов: через эл-ты протекает один и тот же ток Напряжение приложенной ко всей цепи Для послед-ых соединений резистивных Эл-ов Для послед-ых соединенй индуктивных Эл-ов Для послед-ых соединенй емкостных Эл-ов Параллельное соединение элементов: к Эл-м приложено одно и то же напряжение
Для параллельго соед-ия резиствных эл-ов:
Преобразование источника напряжения с параметрами Uг и Rг в эквивалентный источник Iг Gг, или наоборот: Принцип наложения Принцип наложения: Реакция линейной цепи на сумму воздействий равна сумме реакций от каждого воздействия в отдельности. Напряжения и токи источников – воздействия, а напряжения и токи на эл-ах – реакции Исп-ся: для нахождения р-ции в линейной цепи, находящейся как под воздействием неск-их источников, так и при сложном произвольном воздействии одного источника Линейная цепь с нес-кими источниками: результирующая р-ция в соотв-ии с принципом наложения
Если в лин цепи приложено напряжение сложной формы, применение принципа наложения позволяет после разложения этого воздействия на сумму простейших найти р-цию цепи на каждое из них в отдельности с последующим наложением рез-ов МКТ Основан на 2-ом з-не Кирхгофа. МКТ позволяет снизить число решаемых уравнений до числа независимых контуров, определяемых равенством = nв-nу+1-nит Каноническая форму записи ур-ий по МКТ: если цепь содержит к- независимых контуров:
МУП Основывается на 1-ом з-не Кирхгофа и з-не Ома Число ур-ий nу-1
Метод двух узлов
Для цепей, имеющих только два узла 1 и 2. План анализа: 1. Произвольно выбрать направления всех токов в ветвях на исходной схеме. 2. Вычислить узловое напряжение, направленное от узла 1 к узлу 2.
МЭГ В соответствие с т Тевенина и Нортона задающее напряжение генератора определяется как напряжение хх на разомкнутых зажимах активного 2-х-полюсника Uг=Uхх, а задающий ток- как ток кз Iг=Iкз. внутреннее R активного 2-х-полюсника или его проводимость Gг находятся как эквивалентные входные сопротивления или проводимость отн-но разомкнутых зажимов пассивного 2-х-полюсника, к-ый получается после исключения из схемы всех источников напряжения и тока. При этом идеальные источники напряжения закорачиваются, а токи- размыкаются; реальные источники заменяются своими внутренними сопротивлениями или проводимостями.
Индуктивно связанные цепи : изучение методов расчета электрических цепей с взаимной индуктивностью.
10.1 Индуктивно связанные элементы цепи Два элемента индуктивно связаны, если изменение тока в одном элементе приводит к появлению э.д.с. в другом элементе. Возникающая э.д.с. называется э.д.с. взаимной индукции (рисунок 10.1,а,б).
а) б) Рисунок 10.1
При наличии тока i1 в первой катушке, витки первой катушки сцеплены с магнитным потоком самоиндукции Ф11, а витки второй катушки сцеплены с магнитным потоком взаимной индукции Ф21. (рисунок 10.1). Потокосцепления самоиндукции и взаимной индукции первой и второй катушек
где w1,w2- число витков первой и второй катушек. При наличии тока i2 во второй катушке, витки второй катушки сцеплены с магнитным потоком самоиндукции Ф22, а витки первой катушки сцеплены с магнитным потоком взаимной индукции Ф12. Потокосцепления самоиндукции и взаимной индукции второй и первой катушек:
Степень индуктивной связи двух индуктивно связанных элементов цепи характеризуется коэффициентом связи
10.2 Электродвижущая сила (э.д.с.) и напряжение взаимной индукции При изменении тока в одном из индуктивно связанных элементов в другом элементе возникает э.д.с. взаимной индукции ем и на его разомкнутых выводах появляется напряжение uм:
Для определения знака ем и uм делают специальную разметку выводов индуктивно связанных элементов. Два вывода принадлежащие двум разным индуктивно связанным элементам называются одноимёнными и обозначаются одинаковыми значками: **, При одинаковом направлении тока Напряжение взаимной индукции При различном направлении тока
Напряжение взаимной индукции Величина величина
Резонанс токов Резонанс токов возникает в параллельном колебательном контуре при условии, что входная реактивная проводимость
При резонансе токов общий ток наименьший и совпадает с напряжением на входе (рисунок 12.2) Добротность контура
Резонансная частота параллельного колебательного контура По условию резонанса токов где Решая совместно, получим Резонанс токов возможен при а) R1>r; R2>r R1<r; R2<r; б) R1=R2¹r или R1<< r и R2<< r. В случае, когда R1=R2=r получаем неопределенность, т.е. может быть любое значение резонансной частоты. Резонанс, не при какой частоте не возникает, если R1>r, а R2<r или наоборот. Сопротивление параллельного колебательного контура
Эквивалентное сопротивление параллельного колебательного контура
После преобразования Найдем
Частотные характеристики идеального параллельного контура
Так как
Так как ток I=/в/ U, значит в соответствующем масштабе резонансная кривая тока это график Угол
Общее положение 4-х-п – эл цепь, содержащая 2 пары зажимов (4 полюса) и предназначена для передачи эл энергии от генератора к нагрузке. Та пара зажимов, к к-ым подключается генератор, наз. входным Та пара зажимов, к к-ым подключается нагрузка, наз. выходным Классификация 4-х-п: Линейные и нелинейные. Линейные отличаются от нелинейных тем, что не содержат нелинейных эл-ов и поэтому х-ся линейной зав-стью напряжения и тока на выходных зажимах от напряжения и тока на входных зажимах Пассивный активный. Пассивные не содержат источников эл энергии, активные-содержат (завис-ые и незав-ые). Симметричные (перемена местами входных и выходных зажимов не изменяет напряжений и токов в цепи) несимметричные. Мостовые, лестничные (Г,Т,П – образные) Уравновешенные (горизонтальная ось симметрии) неуравновешенные Обратимые (передают энергию в обоих направлениях, т. обратимости: отношение напряжение на входе к току на выходе не меняется при перемене местами зажимов) необратимые Уравнение передачи четырехполюсника Ур-ия, связывающие токи и напряжения на входе и выходе 4-х-п, наз ур-ми передачи 4-х-п Ур-е передачи в А- параметрах:
Ур-е передачи в У- параметрах:
по размерности – проводимость Ур-е передачи в Z- параметрах:
по размерности – сопротивление Ур-е передачи в H- параметрах:
Ур-е передачи в F- параметрах:
Ур-е передачи в В- параметрах:
Параметры холостого хода и короткого замыкания четырехполюсника Параметрами холостого хода (ХХ) и короткого замыкания (КЗ) называются Входные сопротивления четырёхполюсника в режиме холостого хода на зажимах
При коротком замыкании зажимов
Параметры ХХ и КЗ удовлетворяют соотношению:
Характеристические параметры четырехполюсника Высокочастотные фильтры Т-и П- образные схемы высокочастотного фильтра приведены на рисунке 17.4.
Рисунок 17.4 Полоса пропускания Полоса задерживания
Рисунок 17.5 Полосовые фильтры
Т-и П- образные схемы полосового фильтра приведены на рисунке 17.7.
Рисунок 17.7 Выберем
Элементы электрической цепи (активные, пассивные) Эл. цепью наз. совокупность устройств, предназначенных для прохождения тока и описываемых с помощью понятий тока и напряжения Пассивные элементы. Резистивным сопротивлением наз. идеализированный элемент, обладающий только свойством необратимого рассеивания энергии.
Количественной характеристикой: Сопротивление R Ом, проводимость (G=1/R, См) Математическая модель, описывающая св-ва резистивного сопротивления, определяется з-ном Ома: напряжения от тока, наз. вольт-амперной х-кой (ВАХ). Если R постоянно, то ВАХ линейна, если R зав-ит от напряжения и тока, то ВАX нелинейное Мощность в резистивном сопротивлении: Индуктивным эл-ом наз. идеализированный эл-т эл. цепи, обладающий только св-вом накопления им энергии магнитного поля.
Математическая модель, описывающая св-ва индуктивного элемента определяется соотношением Количественная х-ка: индуктивность(положитеьлное). Если L=сonst, зав0ость ВАХ линейная, если зав-ит от тока и напряжения- нелинейная
емкостным эл-от наз. идеализированный эл-т эл цепи, обладающий только св-вом накапливать энергию эл поля.
Математическая модель, описывающая св-ва емкостного эл-та, опред-ся ВАХ: Количественная х-ка: емкость (С)(положительна) Если С=сonst, зав-ость ВАХ линейная, если зав-ит от тока и напряжения- нелинейная
Активные эл-ты: завис-ые и незав-ые источники эл энергии Независимым источником напряжения наз. идеализированный двухполюсный Эл-т, напряжение на зажимах к-ого не зав-ит от протекающего через него тока. Х-ся своим задающим напряжением Uг, или ЭДС ег ВАХ – прямая, параллельная оси токов Независимым источником тока наз идеализированный двухполюсный эл-т, ток к-ого не зав-ит от напряжения на его зажимах Х-ся своим заданный током iг ВАх- прямая, параллельная оси напряжения Зависимый источник - четырехполюсный эл-т с 2-мя парами зажимов- входных и выходных Зависимые источники: источник напряжения, управляемый напряжением; источник тока, управляемый напряжением; источник напряжения, управляемый током; источник тока, управляемый током. Законы Кирхгофа. Закон Ома 1-ый з-н Кирхгофа (з-н токов): алгебраическая сумма токов ветвей, сходящихся в одном узле эл цепи, равна нулю Число независимых ур-ий =nу-1 2-ой з-н Кирхгофа (з-н напряжений): алгебраическая сумма напряжений ветвей в любом контуре равна нулю 2-ой з-н Кирхгофа: (для падении янапряжений): алгебраическая сумма падений напряжений на Эл-ах в замкнутом контуре= алгебраической сумме ЭДС, действующих в данном контуре: Число Ур-ий = nв-nу+1-nит З-н Ома:
3. Преобразование эл схем Последовательное соединение эл-ов: через эл-ты протекает один и тот же ток Напряжение приложенной ко всей цепи Для послед-ых соединений резистивных Эл-ов Для послед-ых соединенй индуктивных Эл-ов Для послед-ых соединенй емкостных Эл-ов Параллельное соединение элементов: к Эл-м приложено одно и то же напряжение
Для параллельго соед-ия резиствных эл-ов:
Преобразование источника напряжения с параметрами Uг и Rг в эквивалентный источник Iг Gг, или наоборот: Принцип наложения Принцип наложения: Реакция линейной цепи на сумму воздействий равна сумме реакций от каждого воздействия в отдельности. Напряжения и токи источников – воздействия, а напряжения и токи на эл-ах – реакции Исп-ся: для нахождения р-ции в линейной цепи, находящейся как под воздействием неск-их источников, так и при сложном произвольном воздействии одного источника Линейная цепь с нес-кими источниками: результирующая р-ция в соотв-ии с принципом наложения
Если в лин цепи приложено напряжение сложной формы, применение принципа наложения позволяет после разложения этого воздействия на сумму простейших найти р-цию цепи на каждое из них в отдельности с последующим наложением рез-ов МКТ Основан на 2-ом з-не Кирхгофа. МКТ позволяет снизить число решаемых уравнений до числа независимых контуров, определяемых равенством = nв-nу+1-nит Каноническая форму записи ур-ий по МКТ: если цепь содержит к- независимых контуров:
МУП Основывается на 1-ом з-не Кирхгофа и з-не Ома Число ур-ий nу-1
Метод двух узлов
Для цепей, имеющих только два узла 1 и 2. План анализа: 1. Произвольно выбрать направления всех токов в ветвях на исходной схеме. 2. Вычислить узловое напряжение, направленное от узла 1 к узлу 2.
МЭГ В соответствие с т Тевенина и Нортона задающее напряжение генератора определяется как напряжение хх на разомкнутых зажимах активного 2-х-полюсника Uг=Uхх, а задающий ток- как ток кз Iг=Iкз. внутреннее R активного 2-х-полюсника или его проводимость Gг находятся как эквивалентные входные сопротивления или проводимость отн-но разомкнутых зажимов пассивного 2-х-полюсника, к-ый получается после исключения из схемы всех источников напряжения и тока. При этом идеальные источники напряжения закорачиваются, а токи- размыкаются; реальные источники заменяются своими внутренними сопротивлениями или проводимостями.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 684; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.36.215 (0.021 с.) |


 Ур-ие определяет зав-сть
Ур-ие определяет зав-сть


 где
где  - потокосцепление
- потокосцепление мгновенная мощность:
мгновенная мощность: 


 Мощность:
Мощность: 
 , где m число ветвей, сходящихся в узле
, где m число ветвей, сходящихся в узле






 Для параллельго соед-ия резиствных эл-ов:
Для параллельго соед-ия резиствных эл-ов: Для параллельго соед-ия емкостных эл-ов:
Для параллельго соед-ия емкостных эл-ов: 
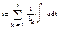

 где n – общее число источников
где n – общее число источников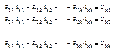
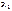 - собственные сопротивления
- собственные сопротивления





 или
или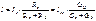

 ,
,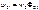
 ;
;  , где w1,w2- число витков первой и второй катушек. Индуктивность первой и второй катушек и их взаимная индуктивность определяются по формулам
, где w1,w2- число витков первой и второй катушек. Индуктивность первой и второй катушек и их взаимная индуктивность определяются по формулам ,
,  ,
,  ,
,  ,
,  . (10.1)
. (10.1) . (10.2)
. (10.2) ;
; 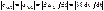 . (10.3)
. (10.3) ,∆∆, если при одинаковом направлении токов в обоих элементах относительно этих выводов магнитные потоки самоиндукции и взаимной индукции в каждом элементе складываются.
,∆∆, если при одинаковом направлении токов в обоих элементах относительно этих выводов магнитные потоки самоиндукции и взаимной индукции в каждом элементе складываются. в элементе 2,
в элементе 2,  ,
,  в элементе 1 и тока
в элементе 1 и тока  в элементе 1,
в элементе 1,  ,
,  в элементе 2 (рисунок 10.1,а)
в элементе 2 (рисунок 10.1,а)  ,
,  , (10.4)
, (10.4)  ,
,  . (10.5)
. (10.5)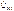 опережает ток
опережает ток 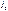 на
на  , напряжение взаимной индукции
, напряжение взаимной индукции  опережает ток
опережает ток  на
на  .
. в элементе 1,
в элементе 1,  ,
,  . (10.6)
. (10.6) ,
,  . (10.7)
. (10.7) на
на  называется сопротивлением взаимной индукции,
называется сопротивлением взаимной индукции, называется комплексным сопротивлением взаимнойиндукции.
называется комплексным сопротивлением взаимнойиндукции.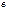
 ,
,  .
.
 ,
,  .
. где
где  -активное сопротивление контура;
-активное сопротивление контура; - полоса пропускания.
- полоса пропускания.  .
.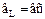
 ,
, 

 , если:
, если:
 где X=XL-XC; R1<< XLR2 << X
где X=XL-XC; R1<< XLR2 << X
 для эквивалентной схемы
для эквивалентной схемы

 то в этом случае резонансная частота
то в этом случае резонансная частота 
 Проводимость катушки
Проводимость катушки  , проводимость конденсатора
, проводимость конденсатора 
 в=вL- вс
в=вL- вс .
. , график
, график 


 безразмерные,
безразмерные,  размерность сопротивления,
размерность сопротивления,  - размерность проводимости
- размерность проводимости


 - безразмерные,
- безразмерные,  - сопротивление, проводимость
- сопротивление, проводимость
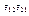 - безразмерные,
- безразмерные,  - проводимости и сопротивления
- проводимости и сопротивления
 и
и  при разомкнутых и замкнутых накоротко зажимах четырёхполюсника.
при разомкнутых и замкнутых накоротко зажимах четырёхполюсника. (ZH2=
(ZH2=  , I2=0) и
, I2=0) и 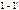 (ZH1=
(ZH1=  ,
, 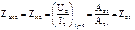 .
. ,
,  .
.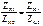 , т.е.только три параметра из четырёх независимы и их достаточно для составления уравнений передачи пассивных четырёхполюсников, из параметров ХХ и КЗ может быть получена любая система параметров-коэффициентов пассивных четырёхполюсников. Для симметричных четырёхполюсников А11=А22, ZX1=ZX2, ZK1=ZK2.
, т.е.только три параметра из четырёх независимы и их достаточно для составления уравнений передачи пассивных четырёхполюсников, из параметров ХХ и КЗ может быть получена любая система параметров-коэффициентов пассивных четырёхполюсников. Для симметричных четырёхполюсников А11=А22, ZX1=ZX2, ZK1=ZK2.

 .
.
 ,
, .
. АЧХ
АЧХ  и ФЧХ
и ФЧХ  для ВЧФ приведены на рисунке 17.5.
для ВЧФ приведены на рисунке 17.5. Полоса пропускания полосового фильтра лежит в диапазоне частот от
Полоса пропускания полосового фильтра лежит в диапазоне частот от  до
до  . Полосовой фильтр может быть образован путём соединения низкочастотного фильтра с полосой пропускания от 0 до
. Полосовой фильтр может быть образован путём соединения низкочастотного фильтра с полосой пропускания от 0 до  , тогда при частоте
, тогда при частоте  в продольной ветви наступает резонанс напряжений, в поперечной резонанс токов. Поэтому частота
в продольной ветви наступает резонанс напряжений, в поперечной резонанс токов. Поэтому частота  принадлежит полосе пропускания. Частотные характеристики полосового фильтра представлены на рисунке 17.8.
принадлежит полосе пропускания. Частотные характеристики полосового фильтра представлены на рисунке 17.8.



