
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Баланс мощности в цепях пост токаСодержание книги Поиск на нашем сайте
Сумма мощности, вырабатываемая независимым источником = сумме мощностей, потребляемыми всеми эл-тами эл цепи
Гармонические колебания в резистивных, индуктивных и емкостных эл-ах Резистивные цепи. Пусть R прилож гарм напр
мощность на R, наз активной Индуктивные цепи. Под действием напряжения Ток в L отстает напр на 90. Фазовый сдвиг между током и напр Сред за период мощность в L =0
Емкостные цепи.
Ток в емкости опережает напряжение на 90, Гармонические колебания в цепи при послед-ом соединении R,L,C- элементов через послед-ые эл-ты протекает ток:
или:
напряжение Uma= Треугольник напряжений: Если Если Если Из треугольник сопротивлений и напряжений следует:
Гармонические колебания в цепи при парал-ом соединении R,L,C- элементов Напряжение: Ток в неразветвленной части ветви:
Ток в резистивном сопротивлении
Если Если Из треугольников токов и проводимостей:
Символический метод расчета разветвленных цепей при гармонической воздействии Для резистивного эл-та по з-ну Ома Для индуктивного эл-та Для емкостного эл-та: Символич. метод при послед соед-ии:
Стмволич. метод при парал-ом соед-ии:
Мощность в цепях синусоидального тока, баланс мощностей Средняя мощность:
Мгновенная мощность Р – активная мощность. Реактивная: Комплексная мощность Модуль комплексной мощности наз полной мощностью Баланс мощности
Частотные х-ки послед-ого колебат контура
При
Частотные х-ки параллельного колебательного контура
резонанс в параллельном контуре возможен: если сопротивление R1 и R2 оба больше или оба меньше Комплексные передаточные ф-ции для эл цепей Комплексная передаточная ф-ция пред-ет собой отношение комплексной амплитуды р-ции (действующ значения р-ции) к комплексной амплитуде воздействия (действующ знаечнию возздействия) 1. Комплексная передаточная ф-ция по напряжению:
2. Комплексная передаточная ф-ция по току:
3. Комплексное передаточное сопротивление:
4. Комплексная передаточная проводимость:
Если и реак-ци яи воздействие приложены к одним и тем же зажима, то комплексные передаточные ф-ции превр-ся в входные
Зав-ть модуля комплексной передаточной ф-ции от частоты наз. АЧХ Зав-ть аргумента к.п.ф. от частоты – ФЧХГраничная частота – чатсота, при к-ой активная составляющая= реактивной Годограф – кривая, точки к-ой соотв-ют при данной частоте АЧх и ФЧХ
Индуктивно связанные цепи : изучение методов расчета электрических цепей с взаимной индуктивностью.
10.1 Индуктивно связанные элементы цепи Два элемента индуктивно связаны, если изменение тока в одном элементе приводит к появлению э.д.с. в другом элементе. Возникающая э.д.с. называется э.д.с. взаимной индукции (рисунок 10.1,а,б).
а) б) Рисунок 10.1
При наличии тока i1 в первой катушке, витки первой катушки сцеплены с магнитным потоком самоиндукции Ф11, а витки второй катушки сцеплены с магнитным потоком взаимной индукции Ф21. (рисунок 10.1). Потокосцепления самоиндукции и взаимной индукции первой и второй катушек
где w1,w2- число витков первой и второй катушек. При наличии тока i2 во второй катушке, витки второй катушки сцеплены с магнитным потоком самоиндукции Ф22, а витки первой катушки сцеплены с магнитным потоком взаимной индукции Ф12. Потокосцепления самоиндукции и взаимной индукции второй и первой катушек:
Степень индуктивной связи двух индуктивно связанных элементов цепи характеризуется коэффициентом связи
10.2 Электродвижущая сила (э.д.с.) и напряжение взаимной индукции При изменении тока в одном из индуктивно связанных элементов в другом элементе возникает э.д.с. взаимной индукции ем и на его разомкнутых выводах появляется напряжение uм:
Для определения знака ем и uм делают специальную разметку выводов индуктивно связанных элементов. Два вывода принадлежащие двум разным индуктивно связанным элементам называются одноимёнными и обозначаются одинаковыми значками: **, При одинаковом направлении тока Напряжение взаимной индукции При различном направлении тока
Напряжение взаимной индукции Величина величина
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.200.78 (0.01 с.) |


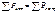
 . По з-ну Ома через R будет протекать ток
. По з-ну Ома через R будет протекать ток , где
, где 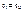 - начальная фаза тока. Ток i и напряжение U в R совпадают по фазе.
- начальная фаза тока. Ток i и напряжение U в R совпадают по фазе.
 в L будет протекать ток:
в L будет протекать ток:  , где
, где  ,
, 

 - индуктивное сопротивление
- индуктивное сопротивление , где
, где 


 . Согласно 2-му з-ну Кирхгофа:
. Согласно 2-му з-ну Кирхгофа: 
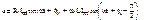


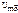 - активная составляющая
- активная составляющая  - реактивная состаляющая
- реактивная состаляющая (
( )- индуктивный х-р
)- индуктивный х-р (
( ) – резистивно-емкостный
) – резистивно-емкостный - резистивный
- резистивный

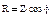
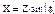



 - активная составляющая,
- активная составляющая,  , а разность тока
, а разность тока 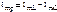 - реактивной составляющей тока
- реактивной составляющей тока - реактивная проводимость цепи
- реактивная проводимость цепи - полная проводимость цепи
- полная проводимость цепи - индуктивный х-р
- индуктивный х-р - емкостной х-р
- емкостной х-р
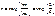

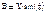


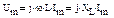 , где
, где 
 или
или 

 - комплексное соединение цепи
- комплексное соединение цепи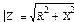 , а фазовый сдвиг:
, а фазовый сдвиг: 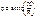

 - комплексная проводимость цепи
- комплексная проводимость цепи


 Вт
Вт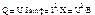 Вар
Вар ВА
ВА





 цепь имеет резистивно-емкостной х-р (X<0
цепь имеет резистивно-емкостной х-р (X<0  ) и ток опережает по фазе приложенное напряжение, при
) и ток опережает по фазе приложенное напряжение, при  х-р цепи резистивно-индуктивный (Х>0
х-р цепи резистивно-индуктивный (Х>0  ) и ток отстает по фазе от приложенного напряжения, при
) и ток отстает по фазе от приложенного напряжения, при  наступает резонанс напряжений (Х=0
наступает резонанс напряжений (Х=0  ) и ток совпадает по фазе с приложенным напряжением
) и ток совпадает по фазе с приложенным напряжением



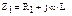
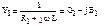

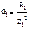


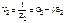



 - при резонансе
- при резонансе


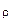 .
.




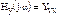


 ,
,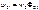
 ;
;  , где w1,w2- число витков первой и второй катушек. Индуктивность первой и второй катушек и их взаимная индуктивность определяются по формулам
, где w1,w2- число витков первой и второй катушек. Индуктивность первой и второй катушек и их взаимная индуктивность определяются по формулам ,
,  ,
,  ,
,  ,
,  . (10.1)
. (10.1) . (10.2)
. (10.2) ;
; 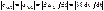 . (10.3)
. (10.3) ,∆∆, если при одинаковом направлении токов в обоих элементах относительно этих выводов магнитные потоки самоиндукции и взаимной индукции в каждом элементе складываются.
,∆∆, если при одинаковом направлении токов в обоих элементах относительно этих выводов магнитные потоки самоиндукции и взаимной индукции в каждом элементе складываются. в элементе 2,
в элементе 2,  ,
,  в элементе 1 и тока
в элементе 1 и тока  в элементе 1,
в элементе 1,  ,
,  в элементе 2 (рисунок 10.1,а)
в элементе 2 (рисунок 10.1,а)  ,
,  , (10.4)
, (10.4)  ,
,  . (10.5)
. (10.5)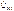 опережает ток
опережает ток 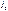 на
на  , напряжение взаимной индукции
, напряжение взаимной индукции  опережает ток
опережает ток  на
на  .
. в элементе 1,
в элементе 1,  ,
,  . (10.6)
. (10.6) ,
,  . (10.7)
. (10.7) на
на  называется сопротивлением взаимной индукции,
называется сопротивлением взаимной индукции, называется комплексным сопротивлением взаимнойиндукции.
называется комплексным сопротивлением взаимнойиндукции.


