
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Последовательное соединение индуктивно связанных элементов цепиСодержание книги
Поиск на нашем сайте
Две индуктивно связанные катушки с сопротивлениями
а) б) Рисунок 10.2
Согласное включение. При согласном включении токи в обоих элементах в любой момент времени направлены одинаково относительно одноименных выводов (рисунок 10.2,а). Поэтому потокосцепления самоиндукции и взаимной индукции в каждом элементе складываются
Индуктивность двух последовательно соединенных индуктивно связанных элементов при согласном включении равна
Напряжение на зажимах первой и второй катушках в комплексной форме
Напряжение на зажимах цепи (рисунок 10.2,а)
где
Векторная диаграмма для согласного включения показана на рисунке 10.3,а. Встречное включение. При встречном включении токи в обоих элементах в любой момент времени направлены различно относительно одноименных выводов (рисунок 10.2,б). Поэтому потокосцепления самоиндукции и взаимной индукции в каждом элементе вычитаются
Напряжение на зажимах первой и второй катушках в комплексной форме
Напряжение на зажимах цепи (рисунок 10.2,б)
где
Векторная диаграмма для встречного включения (при
а) б) Рисунок 10.3
Расчёт разветвлённых цепей при наличии взаимной индуктивности Для разветвлённых цепей с индуктивными связями применяются законы Кирхгофа и метод контурных токов. При составлении уравнений по второму закону Кирхгофа э.д.с. взаимной индукции учитывается как соответствующее напряжение
Рисунок 10.5 Запишем уравнения по второму закону Кирхгофа для схемы (рисунок 10.5).
1 Резонанс напряжений
Где
В зависимости от соотношения величин 1. В цепи преобладает индуктивность, т.е. 2. В цепи преобладает емкость, т.е.
при этом При резонансе напряжений ток в цепи наибольший Как показывает анализ уравнения
Зависимость полного сопротивления контура от частоты
Зависимости
Резонанс токов Резонанс токов возникает в параллельном колебательном контуре при условии, что входная реактивная проводимость
При резонансе токов общий ток наименьший и совпадает с напряжением на входе (рисунок 12.2) Добротность контура
Резонансная частота параллельного колебательного контура По условию резонанса токов где Решая совместно, получим Резонанс токов возможен при а) R1>r; R2>r R1<r; R2<r; б) R1=R2¹r или R1<< r и R2<< r. В случае, когда R1=R2=r получаем неопределенность, т.е. может быть любое значение резонансной частоты. Резонанс, не при какой частоте не возникает, если R1>r, а R2<r или наоборот. Сопротивление параллельного колебательного контура
Эквивалентное сопротивление параллельного колебательного контура
После преобразования Найдем
Частотные характеристики идеального параллельного контура
Так как
Так как ток I=/в/ U, значит в соответствующем масштабе резонансная кривая тока это график Угол
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.93.118 (0.009 с.) |

 ,
,  и индуктивностями
и индуктивностями  соединены последовательно. Возможны два вида включения: согласное и встречное.
соединены последовательно. Возможны два вида включения: согласное и встречное.
 ,
,  .
. (10.8)
(10.8) , (10.9)
, (10.9) . (10.10)
. (10.10) (10.11)
(10.11)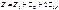 - входное сопротивление цепи при согласном включении;
- входное сопротивление цепи при согласном включении; ;
; ;
; .
. ,
,  . Индуктивность двух последовательно соединенных индуктивно связанных элементов при встречном включении равна
. Индуктивность двух последовательно соединенных индуктивно связанных элементов при встречном включении равна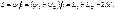 (10.12)
(10.12) , (10.13)
, (10.13) . (10.14)
. (10.14) (10.15)
(10.15) - входное сопротивление цепи при встречном включении;
- входное сопротивление цепи при встречном включении; и
и  ) показана на рисунке 10.3,б.
) показана на рисунке 10.3,б.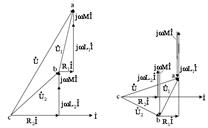
 на элементе К, обусловленное током в элементе S. Напряжение записывается с положительным знаком, если направление обхода элемента К и положительное направление тока в элементе S одинаковы относительно одноимённых выводов.
на элементе К, обусловленное током в элементе S. Напряжение записывается с положительным знаком, если направление обхода элемента К и положительное направление тока в элементе S одинаковы относительно одноимённых выводов.
 }(10.20)
}(10.20)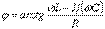


 Резонансом называется такой режим работы цепи, включающей в себя индуктивные и емкостные элементы, при котором ее входное сопротивление вещественно. Следствием этого является совпадение по фазе тока на входе цепи с входным напряжением.
Резонансом называется такой режим работы цепи, включающей в себя индуктивные и емкостные элементы, при котором ее входное сопротивление вещественно. Следствием этого является совпадение по фазе тока на входе цепи с входным напряжением.
 и
и  возможны три различных случая.
возможны три различных случая. , а, следовательно,
, а, следовательно,  .
. , а значит,
, а значит,  .
. - случай резонанса напряжений Условие резонанса напряжений
- случай резонанса напряжений Условие резонанса напряжений 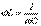 ,
,
 .
. . Соответственно возрастанию тока увеличиваются напряжения на индуктивном и емкостном элементах, которые могут во много раз превысить величину напряжения источника питания. Физическая сущность резонанса заключается в периодическом обмене энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, причем сумма энергий полей остается постоянной.
. Соответственно возрастанию тока увеличиваются напряжения на индуктивном и емкостном элементах, которые могут во много раз превысить величину напряжения источника питания. Физическая сущность резонанса заключается в периодическом обмене энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, причем сумма энергий полей остается постоянной. Добротность Q определяется отношением напряжения на индуктивном (емкостном) элементе в режиме резонанса к входному напряжению
Добротность Q определяется отношением напряжения на индуктивном (емкостном) элементе в режиме резонанса к входному напряжению
 Добротность характеризует “избирательные” свойства резонансного контура, в частности его полосу пропускания
Добротность характеризует “избирательные” свойства резонансного контура, в частности его полосу пропускания  .
.
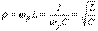 Другим параметром резонансного контура является характеристическое сопротивление, связанное с добротностью соотношением
Другим параметром резонансного контура является характеристическое сопротивление, связанное с добротностью соотношением  Тогда добротность
Тогда добротность 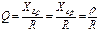 Затухание величина обратная добротности
Затухание величина обратная добротности 
 Зависимость реактивного сопротивления контура от частоты
Зависимость реактивного сопротивления контура от частоты  (рисунок 11.3), где
(рисунок 11.3), где  ,
,  .
.
 ,
,  (рисунок 11.4).До резонанса характер сопротивления контура активно- емкостной, при резонансе активный, после резонанса активно- индуктивный.
(рисунок 11.4).До резонанса характер сопротивления контура активно- емкостной, при резонансе активный, после резонанса активно- индуктивный.
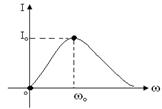 Зависимость
Зависимость 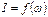 - амплитудно - частотная характеристика (АЧХ),
- амплитудно - частотная характеристика (АЧХ), 


 ,
,  ,
, 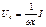

 Зависимость
Зависимость  - фазо- частотная характеристика (ФЧХ),
- фазо- частотная характеристика (ФЧХ), 
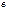
 ,
,  .
.
 ,
,  .
. где
где  -активное сопротивление контура;
-активное сопротивление контура; - полоса пропускания.
- полоса пропускания.  .
.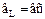
 ,
, 

 , если:
, если:
 где X=XL-XC; R1<< XLR2 << X
где X=XL-XC; R1<< XLR2 << X
 для эквивалентной схемы
для эквивалентной схемы

 то в этом случае резонансная частота
то в этом случае резонансная частота 
 Проводимость катушки
Проводимость катушки  , проводимость конденсатора
, проводимость конденсатора 
 в=вL- вс
в=вL- вс .
. , график
, график 




