
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центрально-растянутые и центрально-сжатые элементыСодержание книги
Поиск на нашем сайте Расчетные длины и предельные гибкости элементов деревянных конструкций 4.21. Для определения расчетной длины прямолинейных элементов, загруженных продольными силами по концам, коэффициент m0 следует принимать равным: при шарнирно-закрепленных концах, а также при шарнирном закреплении в промежуточных точках элемента – 1; при одном шарнирно-закрепленном и другом защемленном конце – 0,8; при одном защемленном и другом свободном нагруженном конце – 2,2; при обоих защемленных концах – 0,65. В случае распределенной равномерно по длине элемента продольной нагрузки коэффициент m0 следует принимать равным: при обоих шарнирно-закрепленных концах – 0,73; при одном защемленном и другом свободном конце – 1,2. Расчетную длину пересекающихся элементов, соединенных между собой в месте пересечения, следует принимать равной: при проверке устойчивости в плоскости конструкций – расстоянию от центра узла до точки пересечения элементов; при проверке устойчивости из плоскости конструкции: а) в случае пересечения двух сжатых элементов – полной длине элемента; б) в случае пересечения сжатого элемента с неработающим – величине l 1, умноженной на коэффициент m0:
где l 1, l1, F 1 – полная длина, гибкость и площадь поперечного сечения сжатого элемента; l 2, l2, F 2 – длина, гибкость и площадь поперечного сечения неработающего элемента. Величину m0 следует принимать не менее 0,5; в) в случае пересечения сжатого элемента с растянутым равной по величине силой – наибольшей длине сжатого элемента, измеряемой от центра узла до точки пересечения элементов. Если пересекающиеся элементы имеют составное сечение, то в формулу (37) следует подставлять соответствующие значения гибкости, определяемые по формуле (11). 4.22. Гибкость элементов и их отдельных ветвей в деревянных конструкциях не должна превышать значений, указанных в табл. 14. Таблица 14
Примечание. Для сжатых элементов переменного сечения величины предельной гибкости lмакс умножаются на Общие указания 5.1. Действующее на соединение (связь) усилие не должно превышать расчетной несущей способности соединения (связи) Т. 5.2. Расчетную несущую способность соединений, работающих на смятие и скалывание, следует определять по формулам: а) из условия смятия древесины Т = R смa F см; (52) б) из условия скалывания древесины
где F см – расчетная площадь смятия; F см – расчетная площадь скалывания; R смa – расчетное сопротивление древесины смятию под углом к направлению волокон;
5.3. Среднее по площадке скалывания расчетное сопротивление древесины скалыванию следует определять по формуле
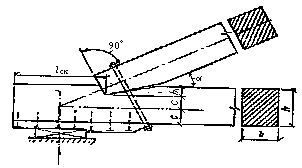
где R ск – расчетное сопротивление древесины скалыванию вдоль волокон (при расчете по максимальному напряжению); l ск – расчетная длина плоскости скалывания, принимаемая не более 10 глубин врезки в элемент; е – плечо сил скалывания, принимаемое равным 0,5 h при расчете элементов с несимметричной врезкой в соединениях без зазора между элементами (рис. 5, а) и 0,25 h при расчете симметрично загруженных элементов с симметричной врезкой (рис. 5, б); (h – полная высота поперечного сечения элемента); b – коэффициент, принимаемый равным 0,25 при расчете соединений, работающих по схеме, показанной на рис. 5, г и b = 0,125 при расчете соединений, работающих по схеме согласно рис. 5, в; если обеспечено обжатие по плоскостям скалывания. Отношение l ск / е должно быть не менее 3.
Рис. 5. Врезки в элементах соединений а – несимметричная; б – симметричная; в, г – схемы скалывания в соединениях Клеевые соединения 5.4. При расчете конструкций клеевые соединения следует рассматривать как неподатливые соединения. 5.5. Клеевые соединения следует использовать: а) для стыкования отдельных слоев на зубчатом соединении (рис. 6, а); б) для образования сплошного сечения (пакетов) путем сплачивания слоев по высоте и ширине сечения. При этом по ширине пакета швы склеиваемых кромок в соседних слоях следует сдвигать не менее чем на толщину слоя d по отношению друг к другу (рис. 6, б); в) для стыкования клееных пакетов, сопрягаемых под углом на зубчатый шип по всей высоте сечения (рис. 6, в).
Рис. 6. Клеевые соединения а – при стыковании отдельных слоев по длине зубчатым шипом, выходящим на пласть; б – при образовании пакетов и сплачивании по пласти и кромке; в – при стыковании клееных элементов под углом зубчатым шипом Величина внутреннего угла между осями сопрягаемых под углом элементов должна быть не менее 104°. 5.6. Применение усового соединения допускается для фанеры вдоль волокон наружных слоев. Длину усового соединения следует принимать не менее 10 толщин стыкуемых элементов. 5.7. Толщину склеиваемых слоев в элементах, как правило, не следует принимать более 33 мм. В прямолинейных элементах допускается толщина слоев до 42 мм при условии устройства в них продольных прорезей. 5.8. В клееных элементах из фанеры с древесиной не следует применять доски шириной более 100 мм при склеивании их с фанерой и более 150 мм в примыканиях элементов под углом от 30 до 45°. Соединения на врубках 5.9. Узловые соединения элементов из брусьев и круглого леса на лобовых врубках следует выполнять с одним зубом (рис. 7).
Рис. 7. Лобовая врубка с одним зубом Рабочая плоскость смятия во врубках при соединении элементов, не испытывающих поперечного изгиба, должна располагаться перпендикулярно оси примыкающего сжатого элемента. Если примыкающий элемент помимо сжатия испытывает поперечный изгиб, рабочую плоскость смятия во врубках следует располагать перпендикулярно равнодействующей осевой и поперечной сил. Элементы, соединяемые на лобовых врубках, должны быть стянуты болтами. 5.10. Лобовые врубки следует рассчитывать на скалывание согласно указаниям пп. 5.2 и 5.3, принимая расчетное сопротивление скалыванию по п. 5 табл. 3. 5.11. Длину плоскости скалывания лобовых врубок следует принимать не менее 1,5 h, где h – полная высота сечения скалываемого элемента. Глубину врубки следует принимать не более 1/4 h в промежуточных узлах сквозных конструкций и не более 1/3 h в остальных случаях, при этом глубина врубок h 1 в брусьях должна быть не менее 2 см, а в круглых лесоматериалах – не менее 3 см. 5.12. Расчет на смятие лобовых врубок с одним зубом следует производить по плоскости смятия (см. рис. 7). Угол смятия древесины a следует принимать равным углу между направлениями сминающего усилия и волокон сминаемого элемента. Расчетное сопротивление древесины смятию под углом к волокнам для лобовых врубок следует определять по формуле (2) примеч. 2 к табл. 3 независимо от размеров площади смятия. Общие указания 6.1. При проектировании деревянных конструкций следует: а) учитывать производственные возможности предприятий-изготовителей деревянных конструкций; б) учитывать возможности транспортных средств; в) использовать древесину с наименьшими отходами и потерями; г) предусматривать меры по обеспечению устойчивости и неизменяемости отдельных конструкций и всего здания или сооружения в целом в процессе монтажа и эксплуатации. 6.2. Напряжения и деформации в деревянных конструкциях от изменения температуры древесины, а также от усушки или разбухания древесины вдоль волокон учитывать не следует. При пролетах деревянных безраспорных конструкций более 30 м одна из опор должна быть подвижной. 6.3. Действие сил трения при расчете деревянных конструкций следует учитывать: а) если равновесие системы обеспечивается только трением при условии постоянного прижатия элемента и отсутствии динамической нагрузки; при этом коэффициент трения дерева по дереву следует принимать равным: торца по боковой поверхности – 0,3; боковых поверхностей – 0,2; б) если трение ухудшает условия работы конструкций и соединений, то коэффициент трения следует принимать равным 0,6. 6.4. В растянутых и изгибаемых элементах из пиломатериалов не следует допускать ослаблений на кромках. 6.5. Расчет элементов из круглых лесоматериалов на устойчивость следует производить по сечению, расположенному в середине расчетной длины элемента, а на прочность – по сечению с максимальным изгибающим моментом. 6.6. Пространственную жесткость и устойчивость деревянных конструкций следует обеспечивать постановкой горизонтальных и вертикальных связей. Поперечные связи следует располагать в плоскости верхнего пояса или по верху несущих конструкций. В качестве поясов связевых ферм следует использовать верхние пояса или все сечение несущих конструкций. 6.7. Размер опорной части плит покрытий должен быть не менее 5,5 см. Плиты покрытий следует прикреплять к несущей конструкции с каждой стороны соединениями, воспринимающими усилия сдвига и отрыва. 6.8. Стыки деревянных растянутых элементов следует осуществлять совмещенными в одном сечении, перекрывая их накладками на стальных цилиндрических нагелях или иных соединениях. Конструкция стыков растянутых элементов должна обеспечивать осевую передачу растягивающего усилия. 6.9. Не следует применять узлы и стыки с соединениями на связях с различной податливости, а также стыки, в которых часть деревянных элементов соединена непосредственно, а часть – через промежуточные элементы и соединения. 6.10. Элементы деревянных конструкций следует центрировать в узлах, стыках и на опорах, за исключением случаев, когда эксцентричное соединение элементов уменьшает действующий в расчетном сечении изгибающий момент. 6.11. Элементы конструкций должны быть стянуты болтами в узлах и стыках, а составные элементы на податливых соединениях должны быть стянуты и между узлами. В соединениях на цилиндрических нагелях должно быть поставлено не менее трех стяжных болтов с каждой стороны стыка. Диаметр стяжных болтов d б следует принимать по расчету, но не менее 12 мм. Шайбы стяжных болтов должны иметь размер сторон или диаметр не менее 3,5 d б и толщину не менее 0,25 d б. 6.12. Площадь поперечного сечения нетто деревянных элементов сквозных несущих конструкций должна быть не менее 50 см2, а также не менее 0,5 полной площади сечения брутто при симметричном ослаблении. Балки, прогоны, настилы 6.13. Балки, прогоны, настилы, обрешетки и другие изгибаемые элементы следует рассчитывать на прочность и прогиб. Значения максимальных прогибов должны быть не выше указанных в табл. 16. 6.14. Настилы и обрешетки под кровлю следует рассчитывать на следующие сочетания нагрузок: а) постоянная и временная от снега (расчет на прочность и прогиб); б) постоянная и временная от сосредоточенного груза 1 кН (100 кгс) с умножением последнего на коэффициент перегрузки n = 1,2 (расчет только на прочность). При сплошном настиле или при разреженном настиле с расстоянием между осями досок или брусков не более 150 мм нагрузку от сосредоточенного груза следует передавать на две доски или бруска, а при расстоянии более 150 мм – на одну доску или брусок. При двойном настиле (рабочем и защитном, направленном под углом к рабочему) сосредоточенный груз следует распределять на ширину 500 мм рабочего настила. 6.15. Подрезка на опоре в растянутой зоне изгибаемых элементов из цельной древесины глубиной а £ 0,25 h допускается при условии
где А – опорная реакция от расчетной нагрузки; b и h – ширина и высота поперечного сечения элемента без подрезки. Длина опорной площадки подрезки с должна быть не больше высоты сечения h, а длина скошенной подрезки c 1 – не менее двух глубин а (рис. 15).
Рис. 15. Скошенная подрезка конца балки 6.16. В консольно-балочных прогонах шарниры следует осуществлять в виде косого прируба. Передачу сосредоточенных нагрузок на несущие элементы конструкций следует осуществлять через их верхние грани. Составные балки 6.17. Составным балкам на податливых связях следует придавать строительный подъем путем выгиба элементов до постановки связей. Величину строительного подъема (без учета последующего распрямления балки) следует принимать увеличенной в полтора раза по сравнению с прогибом составной балки под расчетной нагрузкой. 6.18. Брусчатые составные балки следует сплачивать не более чем из трех брусьев с помощью пластинчатых нагелей. Балки клееные 6.19. Клееным балкам с шарнирным опиранием следует придавать строительный подъем, равный 1/200 пролета. В клееных изгибаемых и сжато-изгибаемых элементах допускается сочетать древесину двух сортов, используя в крайних зонах на 0,15 высоты поперечного сечения более высокий сорт, по которому назначаются расчетные сопротивления (R и, R c). 6.20. Пояса клееных балок с плоской фанерной стенкой следует выполнять из вертикально поставленных слоев (досок). В поясах балок коробчатого сечения допускается применять горизонтальное расположение слоев. Если высота поясов превышает 100 мм, в них следует предусматривать горизонтальные пропилы со стороны стенок. Для стенок балок должна применяться водостойкая фанера толщиной не менее 8 мм. Фермы 6.21. Расчет ферм с разрезными и неразрезными поясами следует производить по деформированной схеме с учетом податливости узловых соединений. В фермах с неразрезными поясами осевые усилия в элементах и перемещения допускается определять в предположении шарнирных узлов. 6.22. Фермы следует проектировать со строительным подъемом не менее 1/200 пролета, осуществляемым в клееных конструкциях путем выгиба по верхнему и нижнему поясам. 6.23. Расчетную длину сжатых элементов ферм при расчете их на устойчивость в плоскости фермы следует принимать равной расстоянию между центрами узлов, а из плоскости – между точками закрепления их из плоскости. 6.24. Элементы решетки ферм следует центрировать в узлах. В случае нецентрированных узлов ферм следует учитывать возникающие в элементах изгибающие моменты. Стыки сжатых поясов ферм следует располагать в узлах или вблизи узлов, закрепленных от выхода из плоскости ферм. Арки и своды 6.25. Арки и своды следует рассчитывать на прочность в соответствии с указаниями п. 4.17 и на устойчивость в плоскости кривизны по формуле (6) п. 4.2 с учетом п. 4.17, причем расчетную длину элементов l о следует принимать: а) при расчете на прочность по деформированной схеме: для двухшарнирных арок и сводов при симметричной нагрузке l о = 0,35 S; для трехшарнирных арок и сводов при симметричной нагрузке l о = 0,58 S; для двухшарнирных и трехшарнирных арок и сводов при кососимметричной нагрузке – по формуле
где a – центральный угол полуарки, рад; S – полная длина дуги арки или свода. Для трехшарнирных стрельчатых арок с углом перелома в ключе более 10° при всех видах нагрузки l о = 0,5 S. При расчете трехшарнирных арок на несимметричную нагрузку расчетную длину допускается принимать равной l о = 0,58 S; б) при расчете на устойчивость в плоскости кривизны для двухшарнирных и трехшарнирных арок и сводов l о = 0,58 S. 6.26. Расчет трехшарнирных арок на устойчивость плоской формы деформирования следует производить по п. 4.18. 6.27. При расчете арок на прочность по деформированной схеме и на устойчивость плоской формы деформирования величины N и М д следует принимать в сечении с максимальным моментом (для проверяемого случая нагружения), а коэффициенты x или xс и xк следует определять по формуле (30) п. 4.17 с подстановкой в нее значения сжимающей силы N о в ключевом сечении арки; расчет арок на устойчивость в плоскости кривизны следует производить по формуле (6) п. 4.2 на ту же сжимающую силу N о. Рамы 6.28. Расчет на прочность элементов трехшарнирных рам в их плоскости допускается выполнять по правилам расчета сжато-изгибаемых элементов с расчетной длиной, равной длине полурамы по осевой линии. 6.29. Устойчивость плоской формы деформирования трехшарнирных рам, закрепленных по внешнему контуру, допускается проверять по формулам п. 4.18. При этом для рам из прямолинейных элементов, если угол между осями ригеля и стойки более 130°, и для гнуто-клееных рам расчетную длину элемента следует принимать равной длине осевой линии полурамы. При угле между стойкой и ригелем меньше 130° расчетную длину ригеля и стойки следует принимать равной длинам их внешних подкрепленных кромок. 6.30. Криволинейные участки гнуто-клееных рам (см. рис. 16) при отношении h / r ³ 1/7 (h – высота сечения, r – радиус кривизны центральной оси криволинейного участка) следует рассчитывать на прочность по формуле (28) п. 4.17, в которой при проверке напряжений по внутренней кромке расчетный момент сопротивления следует умножать на коэффициент kr в:
а при проверке напряжений по наружной кромке – на коэффициент kr н
Расстояние z от центральной оси поперечного сечения до нейтральной оси следует определять по формуле
Рис. 16. Расчетная схема к определению напряжений в криволинейной части гнуто-клееных рам Центрально-растянутые и центрально-сжатые элементы 4.1. Расчет центрально-растянутых элементов следует производить по формуле
где N – расчетная продольная сила; R p – расчетное сопротивление древесины растяжению вдоль волокон; F нт – площадь поперечного сечения элемента нетто. При определении F нт ослабления, расположенные на участке длиной до 200 мм, следует принимать совмещенными в одном сечении. 4.2. Расчет центрально-сжатых элементов постоянного цельного сечения следует производить по формулам: а) на прочность
б) на устойчивость
где R с – расчетное сопротивление древесины сжатию вдоль волокон; j – коэффициент продольного изгиба, определяемый согласно п. 4.3; F нт – площадь нетто поперечного сечения элемента; F рас – расчетная площадь поперечного сечения элемента, принимаемая равной: при отсутствии ослаблений или ослаблениях в опасных сечениях, не выходящих на кромки (рис. 1, а), если площадь ослаблений не превышает 25% Е бр, Е расч = F бр, где F бр – площадь сечения брутто; при ослаблениях, не выходящих на кромки, если площадь ослабления превышает 25% F бр, F рас = 4/3 F нт; при симметричных ослаблениях, выходящих на кромки (рис. 1, б), F рас = F нт.
4.3. Коэффициент продольного изгиба j следует определять по формулам (7) и (8); при гибкости элемента l £ 70
при гибкости элемента l > 70
где коэффициент а = 0,8 для древесины и а = 1 для фанеры; коэффициент А = 3000 для древесины и А = 2500 для фанеры. 4.4. Гибкость элементов цельного сечения определяют по формуле
где l о – расчетная длина элемента; r – радиус инерции сечения элемента с максимальными размерами брутто соответственно относительно осей Х и У. 4.5. Расчетную длину элемента l о следует определять умножением его свободной длины l на коэффициент m0 l о = l m0 (10) согласно пп. 4.21 и 6.25. 4.6. Составные элементы на податливых соединениях, опертые всем сечением, следует рассчитывать на прочность и устойчивость по формулам (5) и (6), при этом F нт и F рас определять как суммарные площади всех ветвей. Гибкость составных элементов l следует определять с учетом податливости соединений по формуле
где lу – гибкость всего элемента относительно оси У (рис. 2), вычисленная по расчетной длине элемента l о без учета податливости; l1 – гибкость отдельной ветви относительно оси I–I (см. рис. 2), вычисленная по расчетной длине ветви l 1; при l 1 меньше семи толщин (h 1) ветви принимаются l1 = 0; mу – коэффициент приведения гибкости, определяемый по формуле
где b и h – ширина и высота поперечного сечения элемента, см: n ш – расчетное количество швов в элементе, определяемое числом швов, по которым суммируется взаимный сдвиг элементов (на рис. 2, а – 4 шва, на рис. 2, б – 5 швов); l о – расчетная длина элемента, м; n с – расчетное количество срезов связей в одном шве на 1 м элемента (при нескольких швах с различным количеством срезов следует принимать среднее для всех швов количество срезов); k с – коэффициент податливости соединений, который следует определять по формулам табл. 12. Таблица 12
Примечание. Диаметры гвоздей и нагелей d, толщину элементов а, ширину b пл и толщину d пластинчатых нагелей следует принимать в см.
При определении k с диаметр гвоздей следует принимать не более 0,1 толщины соединяемых элементов. Если размер защемленных концов гвоздей менее 4 d, то срезы в примыкающих к ним швах в расчете не учитывают. Значение k с соединений на стальных цилиндрических нагелях следует определять по толщине а более тонкого из соединяемых элементов. При определении k с диаметр дубовых цилиндрических нагелей следует принимать не более 0,25 толщины более тонкого из соединяемых элементов. Связи в швах следует расставлять равномерно по длине элемента. В шарнирно-опертых прямолинейных элементах допускается в средних четвертях длины ставить связи в половинном количестве, вводя в расчет по формуле (12) величину n с, принятую для крайних четвертей длины элемента. Гибкость составного элемента, вычисленную по формуле (11), следует принимать не более гибкости l отдельных ветвей, определяемой по формуле
где å Ii бр – сумма моментов инерции брутто поперечных сечений отдельных ветвей относительно собственных осей, параллельных оси У (см. рис. 2); F бр – площадь сечения брутто элемента; l о – расчетная длина элемента. Гибкость составного элемента относительно оси, проходящей через центры тяжести сечений всех ветвей (ось Х на рис. 2), следует определять как для цельного элемента, т. е. без учета податливости связей, если ветви нагружены равномерно. В случае неравномерно нагруженных ветвей следует руководствоваться п. 4.7. Если ветви составного элемента имеют различное сечение, то расчетную гибкость l1 ветви в формуле (11) следует принимать равной:
определение l 1 приведено на рис. 2. 4.7. Составные элементы на податливых соединениях, часть ветвей которых не оперта по концам, допускается рассчитывать на прочность и устойчивость по формулам (5), (6) при соблюдении следующих условий: а) площади поперечного сечения элемента F нт и F рас следует определять по сечению опертых ветвей; б) гибкость элемента относительно оси У (см. рис. 2) определяется по формуле (11); при этом момент инерции принимается с учетом всех ветвей, а площадь – только опертых; в) при определении гибкости относительно оси Х (см. рис. 2) момент инерции следует определять по формуле I = I о + 0,5 I но, (15) где I о и I но – моменты инерции поперечных сечений соответственно опертых и неопертых ветвей. 4.8. Расчет на устойчивость центрально-сжатых элементов переменного по высоте сечения следует выполнять по формуле
где F макс – площадь поперечного сечения брутто с максимальными размерами; k ж N – коэффициент, учитывающий переменность высоты сечения, определяемый по табл. 1 прил. 4 (для элементов постоянного сечения k ж N = 1); j – коэффициент продольного изгиба, определяемый по п. 4.3 для гибкости, соответствующей сечению с максимальными размерами. Изгибаемые элементы 4.9. Расчет изгибаемых элементов, обеспеченных от потери устойчивости плоской формы деформирования (см. пп. 4.14 и 4.15), на прочность по нормальным напряжениям следует производить по формуле
где М – расчетный изгибающий момент; R и – расчетное сопротивление изгибу; W рас – расчетный момент сопротивления поперечного сечения элемента. Для цельных элементов W рас = W нт; для изгибаемых составных элементов на податливых соединениях расчетный момент сопротивления следует принимать равным моменту сопротивления нетто W нт, умноженному на коэффициент k w; значения k w для элементов, составленных из одинаковых слоев, приведены в табл. 13. При определении W нт ослабления сечений, расположенные на участке элемента длиной до 200 мм, принимают совмещенными в одном сечении. Таблица 13
Примечание. Для промежуточных значений величины пролета и числа слоев коэффициенты определяются интерполяцией. 4.10. Расчет изгибаемых элементов на прочность по скалыванию следует выполнять по формуле
где Q – расчетная поперечная сила; S бр – статический момент брутто сдвигаемой части поперечного сечения элемента относительно нейтральной оси; I бр – момент инерции брутто поперечного сечения элемента относительно нейтральной оси; b рас – расчетная ширина сечения элемента; R ск – расчетное сопротивление скалыванию при изгибе. 4.11. Количество срезов связей n с, равномерно расставленных в каждом шве составного элемента на участке с однозначной эпюрой поперечных сил, должно удовлетворять условию
где Т – расчетная несущая способность связи в данном шве; М А, М В – изгибающие моменты в начальном А и конечном В сечениях рассматриваемого участка. Примечание. При наличии в шве связей разной несущей способности, но одинаковых по характеру работы (например, нагелей и гвоздей), несущие способности их следует суммировать. 4.12. Расчет элементов цельного сечения на прочность при косом изгибе следует производить по формуле
где М х и М у – составляющие расчетного изгибающего момента для главных осей сечения Х и У; W x и W у – моменты сопротивлений поперечного сечения нетто относительно главных осей сечения Х и У. 4.13. Клееные криволинейные элементы, изгибаемые моментом М, уменьшающим их кривизну, следует проверять на радиальные растягивающие напряжения по формуле
где s0 – нормальное напряжение в крайнем волокне растянутой зоны; s i – нормальное напряжение в промежуточном волокне сечения, для которого определяются радиальные растягивающие напряжения; hi – расстояние между крайним и рассматриваемым волокнами; ri – радиус кривизны линии, проходящей через центр тяжести части эпюры нормальных растягивающих напряжений, заключенной между крайним и рассматриваемым волокнами; R р.90 – расчетное сопротивление древесины растяжению поперек волокон, принимаемое по п. 7 табл. 3. 4.14. Расчет на устойчивость плоской формы деформирования изгибаемых элементов прямоугольного постоянного сечения следует производить по формуле
где М – максимальный изгибающий момент на рассматриваемом участке l р; W бр – максимальный момент сопротивления брутто на рассматриваемом участке l p. Коэффициент jМ для изгибаемых элементов прямоугольного постоянного поперечного сечения, шарнирно-закрепленных от смещения из плоскости изгиба и закрепленных от поворота вокруг продольной оси в опорных сечениях, следует определять по формуле
где l p – расстояние между опорными сечениями элемента, а при закреплении сжатой кромки элемента в промежуточных точках от смещения из плоскости изгиба – расстояние между этими точками; b – ширина поперечного сечения; h – максимальная высота поперечного сечения на участке l p; k ф – коэффициент, зависящий от формы эпюры изгибающих моментов на участке l p, определяемый по табл. 2 прил. 4 настоящих норм. При расчете изгибаемых элементов с линейно меняющейся по длине высотой и постоянной шириной поперечного сечения, не имеющих закреплений из плоскости по растянутой от момента М кромке, или при m < 4 коэффициент j М по формуле (23) следует умножать на дополнительный коэффициент k ж М . Значения k ж М приведены в табл. 2 прил. 4. При m ³ 4 k ж М = 1. При подкреплении из плоскости изгиба в промежуточных точках растянутой кромки элемента на участке l p коэффициент j М определенный по формуле (23), следует умножать на коэффициент k п М :
где ap – центральный угол в радианах, определяющий участок l p элемента кругового очертания (для прямолинейных элементов ap = 0); m – число подкрепленных (с одинаковым шагом) точек растянутой кромки на участке l p (при m ³ 4 величину 4.15. Проверку устойчивости плоской формы деформирования изгибаемых элементов постоянного двутаврового или коробчатого поперечного сечений следует производить в тех случаях, когда l p ³ 7 b, (25) где b – ширина сжатого пояса поперечного сечения. Расчет следует производить по формуле
где j – коэффициент продольного изгиба из плоскости изгиба сжатого пояса элемента, определяемый по п. 4.3; R с – расчетное сопротивление сжатию; W бр – момент сопротивления брутто поперечного сечения; в случае фанерных стенок – приведенный момент сопротивления в плоскости изгиба элемента.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 490; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |

 , (37)
, (37) , где коэффициент k ж N принимается по табл. 1 прил. 4.
, где коэффициент k ж N принимается по табл. 1 прил. 4. , (53)
, (53) – расчетное среднее по площадке скалывания сопротивление древесины скалыванию вдоль волокон, определяемое п. 5.3.
– расчетное среднее по площадке скалывания сопротивление древесины скалыванию вдоль волокон, определяемое п. 5.3. , (54)
, (54)

 < 0,4 МПа = 4 кгс/см2, (61)
< 0,4 МПа = 4 кгс/см2, (61)
 , (62)
, (62) , (63)
, (63) . (64)
. (64) . (65)
. (65)
 , (4)
, (4) ; (5)
; (5) , (6)
, (6)
 ; (7)
; (7) , (8)
, (8) , (9)
, (9) , (11)
, (11) , (12)
, (12)
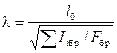 , (13)
, (13) , (14)
, (14) , (16)
, (16)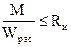 , (17)
, (17) , (18)
, (18) , (19)
, (19) , (20)
, (20)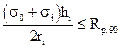 , (21)
, (21) , (22)
, (22) , (23)
, (23) , (24)
, (24) следует принимать равной 1).
следует принимать равной 1).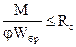 , (26)
, (26)


