
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Получение синусоидального напряжения и его параметрыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Промышленными источникамисинусоидального тока являются электромеханические генераторы, в которых механическая энергия паровых и гидравлических турбин преобразуется в электрическую. Пусть имеется однородное магнитное поле, образованное между полюсами N – S электромагнита. Внутри поля под действием посторонней силы вращается по окружности в сторону движения против часовой стрелки металлический прямолинейный проводник. Как известно, пересечение проводником магнитных линий приведет к появлению а проводнике индуцируемой ЭДС. Величина этой ЭДС зависит от величины магнитной индукции В, активной длины проводника l, скорости пересечения проводником магнитных линий v (
При движении проводник занимает различные положения при этом меняется значение угла, а в мести с ним и значение ЭДС, определяемое по правилу правой руки. За один полный оборот проводника ЭДС в нем сначала увеличивается от нуля до максимального значения (Em), а затем уменьшается до нуля и, изменив свое направление, вновь уменьшается до максимального значения (-Em) и вновь уменьшается до нуля. При дальнейшем движении проводника указанные изменения ЭДС будут повторятся.
Рис.. Амплитуда - это максимальное значение периодически изменяющейся величины. Обозначаются амплитуды прописными буквами с индексом m, т. е. Еm, Um и Im. На основании рис. Можно сделать вывод, что ЭДС достигает своих амплитудных значений тогда, когда рамка повернется на угол α = 90° или на угол α = 270°, так как |sin 90°| = |sin 270°| = 1. Следовательно
Период - это время, в течение которого переменная величина делает полный цикл своих изменений, после чего изменения повторяются в той же последовательности. Обозначается период буквой Т и измеряется в секундах, т.е. [ Т ] = с. Частота - число периодов в единицу времени, т. е. величина, обратная периоду. Обозначается частота буквой f,
Стандартной частотой в электрических сетях России является частота f = 50 Гц. Для установок электронагрева пользуются частотами f = 50 ÷ 50·106 Гц. При частоте f = 50 Гц, т. е. 50 периодов в секунду, период
Угловая частота (угловая скорость) характеризуется углом поворота рамки в единицу времени. Обозначается угловая частота буквой ω (омега):
Измеряется угловая частота в единицах радиан в секунду (рад/с), так как угол измеряется в радианах (рад). За время одного периода Т рамка повернется на угол 360° = 2π рад. Следовательно, угловую частоту можно выразить следующим образом:
Мгновенное значение - это значение переменной величины в любой конкретный момент времени. Мгновенные значения обозначаются строчными буквами, т. е. e, i, u. Из выражения (10.2) следует, что угол поворота рамки
Таким образом, любая синусоидальная величина характеризуется амплитудой и угловой частотой, которые являются постоянными для данной синусоиды. Следовательно, по формулам (10.4) можно определить синусоидальную величину в любой конкретный момент времени t, если известны амплитуда и угловая частота.
Если в магнитном поле вращаются две жестко скрепленные между собой под каким-то углом одинаковые рамки (рис. 10.4а) т. е. амплитуды ЭДС Ет и угловые частоты со их одинаковы, то мгновенное значение их ЭДС можно записать в виде
где ψ1 и ψ2 - углы, определяющие значения синусоидальных величин е1 и е2 в начальный момент времени (t = 0), т. е.
Поэтому эти углы ψ1 и ψ2 называют начальными фазами синусоид.
Рис. 10.4
Начальные фазы ψ1 и ψ2 этих ЭДС различны. Таким образом, согласно (10.5) каждая синусоидальная величина характеризуется амплитудой Еm, угловой частотой ω и начальной фазой ψ. Для каждой синусоиды эти величины (Еm, ω и ψ) являются постоянными. В выражениях (10.4) начальные фазы ψ синусоид равны нулю. Величина Разность начальных фаз двух синусоидальных величин одинаковой частоты определяет угол сдвига фаз этих величин:
При вращении против часовой стрелки (рис. 10.4а) ЭДС в первой рамке достигает амплитудного и нулевого значения раньше чем во второй, т. е. е1 опережает по фазе е2 или е2 отстает по фазе от е1 (рис. 10.46). Угол сдвига фаз Две синусоидальные величины одинаковой частоты, достигающие одновременно своих амплитудных (одного знака) и нулевых значений, считаются совпадающими по фазе (рис. 10.5а).
Рис. 10.5
Если две синусоиды одинаковой частоты достигают одновременно своих нулевых и амплитудных значений разных знаков (рис. 10.56), то они находятся в противофазе.
Среднее значение переменного тока равно величине такого постоянного тока, при котором через поперечное сечение проводника проходит то же количество электричества, что и при переменном токе. Таким образом, среднее значение переменного тока эквивалентно постоянному току по количеству электричества Q, проходящему через поперечное сечение проводника в определенный промежуток времени. Средние значения переменных величин обозначаются прописными буквами с индексом «с», т. е. IC, UC, ЕC. Если ток изменяется по синусоидальному закону, то за половину периода через поперечное сечение проводника проходит определенное количество электричества Q в определенном направлении, а за вторую половину периода через то же сечение проходит то же количество электричества в обратном направлении. Таким образом, среднее значение синусоидального тока за период равно нулю, т. е. IC = 0.
Рис. 10.6
Поэтому для синусоидального переменного тока определяется его среднее значение за половину периода Т/2, т. е.
Значение переменного тока определяется выражением
Где Средние значения синусоидального напряжения и ЭДС за полупериод можно определить по аналогии с током.
Действующее (или эффективное) значение переменного тока - это значение переменного тока, эквивалентное постоянному току по тепловому действию. Действующее значения переменных величин обозначается прописными буквами без индексов: I, U, E. Действующее значение переменного тока I равно величине такого постоянного тока, которое за время, равное одному периоду переменного тока Т, выделит в том же сопротивлении R такое же количество тепла, что и переменный ток I:
Откуда действующее значение переменного тока
Если переменный ток изменяется по синусоидальному закону с начальной фазой, равной нулю, т.е.
Действующее значение синусоидального тока в
Номинальные значения тока и напряжения в электрических цепях и устройствах выражаются их действующими значениями. Так, например, стандартные напряжения электрических сетей U = 127 В или U = 220 В выражают действующие значения этих напряжений. А изоляцию необходимо рассчитывать на амплитудное значение этих напряжений, т. е.
При расчете цепей переменного тока и их исследованиях чаще всего пользуются действующими (эффективными) значениями тока, напряжения и ЭДС. На шкалах измерительных приборов переменного тока указывается действующие значение переменного тока или напряжения. Именно действующие значения тока, напряжения и ЭДС указываются в технической документации, если нет специальных оговорок.
Пусть магнитный поток постоянного магнита равен Фm. Из пространственного расположения магнитного потока следует, что мгновенное значение составляющей магнитного потока, пронизывающей виток, т.е. направленной вдоль оси х, равно
где Ф m – максимальное значение (амплитуда) магнитного потока, пронизывающего виток; a - начальный (т.е. в момент t = 0 принятый за начало отсчета времени) угол пространственного расположения постоянного магнита относительно оси х; jФ - начальная фаза магнитного потока,
Согласно закону электромагнитной индукции при изменении потокосцепления витка в нем индуцируется ЭДС
Подставляя сюда (1), имеем
где
Синусоидальные величины принято изображать графически в виде зависимости
Если начальная фаза >0, то начало синусоидальной величины сдвинуто влево, если <0, то – вправо от начала координат. Если к выводам «а» и «в» генератора подключить резистор, то в полученной цепи возникнет синусоидальный ток i.
Коэффициент мощности Номинальные параметры, т. е. мощность источника SИСТ, мощность потребителя РПОТР и коэффициент мощности cosφПОТР, связаны следующим соотношением
Из (1) следует, что чем меньше cosφПОТР, тем большую мощность S должен иметь источник для питания этого потребителя, т. е. тем больше его габариты, вес, расход материалов, стоимость и д.р. Ток в цепи потребителя с определенным cosφПОТР равен
Из (2) видно, что чем меньше cosφПОТР, тем больше ток потребителя I, тем больший ток проходит по проводам линии электропередачи, тем больше потери энергии в этой линии и меньше КПД ее и всей системы. Кроме того, увеличение тока требует для его передачи проводов большего сечения, т. е. большего расхода цветных металлов. Таким образом, низкий коэффициент мощности потребителя cosφПОТР, приводит к увеличению мощности источника, питающего этот потребитель, уменьшению КПД линии электропередачи и к увеличению сечения проводов линий электропередачи. В России установлен минимально допустимый коэффициент мощности не менее 0,93, т. е. cosφПОТР должен быть равен или больше 0,93 (cosφПОТР > 0,93). Однако cosφПОТР, большинства электрических потребителей переменного тока меньше этой нормы. Так, например, cosφПОТР асинхронных двигателей, в зависимости от нагрузки, составляет 0,2-0,85, трансформаторов - 0,5-0,9, выпрямителей - 0,7-0,85 и т. д. Следовательно, коэффициент мощности этих потребителей необходимо повышать. Так как большинство потребителей представляет собой нагрузку индуктивного характера, то для улучшения cosφПОТР параллельно с ним подключаются конденсаторы (рис. 13.5а).
Рис. 13.5.
Из векторной диаграммы (рис. 13.5б) видно, что с подключением конденсатора С (ключ К замкнут) появляется IC, за счет которого уменьшается угол φ (φ<φН) и увеличивается cosφ установки. При этом уменьшается ток цепи I, который до подключения конденсатора был равен току нагрузки IН. Для повышения коэффициента мощности (cosφ) конденсатор можно включить последовательно с потребителем индуктивного характера. Однако при этом нарушается режим работы (напряжение) потребителя. Поэтому для улучшения cosφ конденсатор подключают параллельно с нагрузкой (рис. 13.5а). Коэффициент мощности можно повысить, увеличив активную нагрузку. При этом увеличивается потребляемая энергия, что экономически нерационально (уменьшается КПД установки). Энергетические процессы в резистивном, индуктивном и емкостном элементе Мгновенная мощность в цепи с активным сопротивлением определяется произведением мгновенных значений напряжения и тока, т. е.
Рис. Изменение мощности в активном сопротивлении.
Мощность в цепи с активным сопротивлением изменяется по величине, но не изменяется по направлению. Эта мощность (энергия) необратима. От источника она поступает потребителю и полностью преобразуется в другие виды мощности (энергии), т.е. потребляется. Такая потребляемая мощность называется активной. Поэтому и сопротивление R, на котором происходит подобное преобразование, называется активным сопротивлением. В цепи с активным сопротивлением мгновенная мощность характеризует скорость преобразования электрической энергии в другие виды энергии. Количественно мощность в цепи с активным сопротивлением определяется следующим образом:
Мгновенная мощность в цепи синусоидального тока с активным сопротивлением представляет собой сумму двух величин - постоянной мощности UI и переменной Средняя за период мощность, равная постоянной составляю, щей мгновенной мощности UI, является активной мощностью P. Среднее за период значение переменной составляющей, как и всякой синусоидальной величины, равно нулю, то есть Таким образом, величина активной мощности в цепи синусоидального тока с активным сопротивлением с учетом закона Ома определяется выражением:
где U - действующее значение напряжения; I - действующее значение тока. Единицей активной мощности является ватт:
Мгновенная мощность для цепи синусоидального тока с идеальной катушкой равна произведению мгновенных значений напряжения и тока
где Следовательно,
Таким образом, мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой. То есть в 1-ю и 3-ю четверти периода мощность (энергия) источника накапливается в магнитном поле индуктивности. Максимальное значение накапливаемой в магнитном поле идеальной катушки энергии равно
Во 2-ю и 4-ю четверти периода эта мощность (энергия) из магнитного поля идеальной катушки возвращается к источнику.
Рис. Изменение мощности в катушке индуктивности..
Следовательно, среднее значение этой мощности за период РС, как и любой синусоидальной величины, т. е. активная потребляемая мощность, в этой цепи равна нулю, Р = 0. Таким образом, в цепи переменного тока с идеальной катушкой, мощность не потребляется (Р = 0), а колеблется между источником и магнитным полем индуктивности, загружая источник и провода. Такая колеблющаяся мощность (энергия), в отличие от активной, т. е. потребляемой, называется реактивной. Обозначается реактивная мощность буквой Q и измеряется в варах, т.е. [ Q ] = вар (вольт-ампер реактивный). Величина реактивной мощности в рассматриваемой цепи определяется выражением
Так как реактивная мощность QL имеет место в цепи с индуктивным сопротивлением, то индуктивное сопротивление считается реактивным сопротивлением X индуктивного характера (индекс L), т.е. ХL.
Если в цепи конденсатора емкостью С, RC = 0 проходит ток i, изменяющийся по синусоидальному закону:
то напряжение u, приложенное к этому конденсатору, будет равно
Мгновенная мощность в цепи с конденсатором
Мощность в цепи с конденсатором, подключенным к источнику с синусоидальным напряжением, изменяется по синусоидальному закону с двойной частотой. Следовательно, активная мощность Р в рассматриваемой цепи, равная среднему значению мгновенной мощности за период, имеет нулевое значение, Р = 0. Во 2-ю и 4-ю четверти периода мощность (энергия) источника накапливается в электрическом поле конденсатора. Максимальное значение энергии, накапливаемой в электрическом поле конденсатора, равно
В 1-ю и 3-ю четверти периода эта мощность (энергия) из электрического поля конденсатора возвращается к источнику.
Рис. Изменение мощности в емкостном элементе.
Таким образом, в цепи переменного тока с конденсатором происходит колебание мощности (энергии) между источником и электрическим полем конденсатора. Величина реактивной мощности в цепи конденсатора определяется выражением
Реактивная мощность в цепи конденсатора изменяется в противофазе с реактивной мощностью в цепи с идеальной катушкой. Отсюда и знак «минус» в уравнении - аналитическом выражении мгновенной мощности в цепи с конденсатором. Так как реактивная мощность QC имеет место в цепи с емкостным сопротивлением, то это емкостное сопротивление считается реактивным сопротивлением X емкостного характера (ХC). Полная мощность определяет эксплуатационные возможности многих электротехнических устройств. Связь между активной, реактивной и полной мощностью видно из выражения
Она измеряется в вольт-амперах Таким образом, чем больше значения U и I, на которое рассчитаны генераторы и трансформаторы, тем больше должны быть их размеры.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 3488; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.015 с.) |

 ;
;  ;
; 
 ) и синуса угла α между направлением движением проводника и направлением магнитного поля:
) и синуса угла α между направлением движением проводника и направлением магнитного поля:


 (10.1)
(10.1) , и измеряется в герцах (Гц):
, и измеряется в герцах (Гц):
 c
c (10.2)
(10.2) (10.3)
(10.3) , тогда мгновенные значения синусоидальных величин можно зависать так:
, тогда мгновенные значения синусоидальных величин можно зависать так: ;
;  ;
;  . (10.4)
. (10.4) ;
;  (10.5)
(10.5) ;
; 

 называется фазой синусоиды.
называется фазой синусоиды. (10.6)
(10.6) показывает, на какой угол одна синусоидальная величина опережает или отстает от другой (т.е. достигает своих амплитудных и нулевых значений раньше или позже).
показывает, на какой угол одна синусоидальная величина опережает или отстает от другой (т.е. достигает своих амплитудных и нулевых значений раньше или позже).



 , откуда
, откуда  . Следовательно, среднее значение синусоидального тока
. Следовательно, среднее значение синусоидального тока 
 , а
, а  . Графически среднее за полупериод значение синусоидального тока равно высоте прямоугольника с основанием, равным Т/2, и площадью, равной площади, ограниченной кривой тока и осью абсцисс за половину периода (рис. 10.6). Под средним значением переменной величины понимают постоянную составляющую этой величины.
. Графически среднее за полупериод значение синусоидального тока равно высоте прямоугольника с основанием, равным Т/2, и площадью, равной площади, ограниченной кривой тока и осью абсцисс за половину периода (рис. 10.6). Под средним значением переменной величины понимают постоянную составляющую этой величины. ;
;  ;
;  (10.8)
(10.8)
 или
или 

 =1,41 раза меньше его амплитудного значения. Так же можно определить действующие значения синусоидального напряжения и ЭДС.
=1,41 раза меньше его амплитудного значения. Так же можно определить действующие значения синусоидального напряжения и ЭДС. ;
;  ;
;  (10.9)
(10.9) В или
В или  В.
В. (1)
(1) ;
; - фаза магнитного потока. Здесь и в дальнейшем начальная фаза определяет значение синусоидальной величины в момент времени t = 0.
- фаза магнитного потока. Здесь и в дальнейшем начальная фаза определяет значение синусоидальной величины в момент времени t = 0.

 - амплитуда ЭДС,
- амплитуда ЭДС, 
 - начальная фаза ЭДС,
- начальная фаза ЭДС, 
 . Поэтому начальная фаза определяет смещение синусоидальной величины относительно начала координат т.е. от
. Поэтому начальная фаза определяет смещение синусоидальной величины относительно начала координат т.е. от  .
.
 (1)
(1) (2)
(2)
 .
.

 , изменяющейся с двойной частотой.
, изменяющейся с двойной частотой. .
.



 . Полученное уравнение умножают и делят на 2:
. Полученное уравнение умножают и делят на 2:




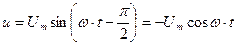




 . Величина полной мощности, равна произведению U·I, определяет основные габариты генераторов и трансформаторов. В самом деле, величина тока I определяет необходимое по условиям нагрева сечение проводов генераторов и трансформаторов, а число витков обмоток, их изоляция, а также размеры магнитопроводов пропорциональны величине напряжения U.
. Величина полной мощности, равна произведению U·I, определяет основные габариты генераторов и трансформаторов. В самом деле, величина тока I определяет необходимое по условиям нагрева сечение проводов генераторов и трансформаторов, а число витков обмоток, их изоляция, а также размеры магнитопроводов пропорциональны величине напряжения U.


