
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрические цепи однофазного синусоидального токаСодержание книги
Поиск на нашем сайте
2.1. Основные определения. Изображения синусоидальных функций времени векторами на комплексной плоскости Переменным током называется ток, величина и направление которого изменяются во времени. Широкое применение переменного тока в электроэнергетике объясняется необходимостью централизованного производства электрической энергии и передачи ее на значительные расстояния. Для уменьшения потерь при передаче энергии требуется использование высокого напряжения, а распределение энергии потребителям по условиям безопасности выполняется при сравнительно низком напряжении. Преобразование переменного напряжения выполняется с помощью трансформаторов, обладающих высоким КПД и надежностью. В электроэнергетике России и Европы принята стандартная частота переменных токов 50 Гц, в США и Японии - 60 Гц. Значение переменного тока в рассматриваемый момент времени называют мгновенным значением и обозначают строчной буквой i. Переменный ток является периодическим, если значения его повторяются через одинаковые промежутки времени i(t)=i(t+T). Наименьший промежуток времени, через который значения переменного тока повторяются, называется периодом. Период T измеряется в секундах. Периодические токи, изменяющиеся по синусоидальному закону, называются синусоидальными. Мгновенное значение синусоидального тока определяется выражением
где Im - максимальное или амплитудное значение тока. Аргумент синусоидальной функции (2.1)  называют круговой или угловой частотой. Круговая частота измеряется в рад/c. называют круговой или угловой частотой. Круговая частота измеряется в рад/c.
Амплитудное значение синусоидального тока или напряжения, его фазу и частоту можно измерить с помощью электронного осциллографа. Действующим значением переменного тока называется среднеквадратичное значение тока за период. Действующее значение тока для синусоидального тока
Аналогично (2.2) определяются действующие значения ЭДС и напряжений:
Действующие значения переменного тока, напряжения, ЭДС меньше их амплитудных значений в √2 раз. Действующее значение синусоидального тока (2.2) численно равно значению постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, как синусоидальный ток. Для мгновенных значений переменных токов и напряжений справедливы рассмотренные ранее законы Кирхгофа. Алгебраическая сумма мгновенных значений токов в узле равна нулю (первый закон Кирхгофа):
Алгебраическая сумма мгновенных значений ЭДС всех источников напряжения в замкнутом контуре равна алгебраической сумме мгновенных напряжений на элементах этого контура (второй закон Кирхгофа):
При расчете электрических цепей часто приходится складывать или вычитать величины токов или напряжений, являющиеся синусоидальными функциями времени. Графические построения или тригонометрические преобразования в этом случае могут оказаться слишком громоздкими. Пусть отрезок прямой длиной Im начинает вращаться вокруг оси 0 из положения, когда он образует с горизонтальной осью угол φ, и вращается против часовой стрелки с постоянной угловой скоростью ω. Проекция отрезка на вертикальную ось в начальный момент времени Пусть даны два синусоидальных тока:
Нужно сложить эти токи и получить результирующий ток:
Рис. 2.1 Представим синусоидальные токи i 1 и i 2 в виде двух радиус - векторов, длина которых равна в соответствующем масштабе I 1 m и I 2 m . Эти векторы расположены в начальный момент времени под углами φ1 и φ2 относительно горизонтальной оси. Сложим геометрически отрезки I 1 m и I 2 m . Получим отрезок, длина которого равна амплитудному значению результирующего тока I 3 m . Отрезок расположен под углом φ3 относительно горизонтальной оси. Все три отрезка вращаются вокруг оси 0 с постоянной угловой скоростью ω. Проекции отрезков на вертикальную ось изменяются по синусоидальному закону. Будучи остановленными, данные отрезки образуют векторную диаграмму (рис. 2.2). Векторная диаграмма - это совокупность векторов, изображающих синусоидальные напряжения, токи и ЭДС одинаковой частоты.
Необходимо отметить, что напряжение, ток и ЭДС - это скалярные, а не векторные величины. Мы представляем их на векторной диаграмме в виде не пространственных, а временных радиус - векторов, вращающихся с одинаковой угловой скоростью. Положительным считается направление вращения векторов против часовой стрелки. Изображать на векторной диаграмме два вектора, вращающихся с различной угловой скоростью, нельзя.
Рис. 2.2 При расчетах цепей синусоидального тока используют символический метод расчета или метод комплексных амплитуд, в котором синусоидально изменяющиеся функции изображаются векторами на комплексной плоскости. Из курса математики известно, что комплексное число может быть записано в показательной или алгебраической форме:
где с - модуль комплексного числа; φ- аргумент; a=Re ( С помощью формулы Эйлера можно перейти от показательной формы записи комплексного числа к алгебраической:
От алгебраической формы записи переходят к показательной форме с помощью формул:
Комплексное число может быть представлено в виде радиус - вектора на комплексной плоскости с длиной, равной модулю c, расположенного в начальный момент времени под углом φ относительно вещественной оси (рис.2.3).
Рис. 2.3 Умножим комплексное число на множитель ej β. Радиус - вектор на комплексной плоскости повернется на угол βпротив часовой стрелки. Множитель ej β называется поворотным:
Отметим очевидные соотношения при следующих значениях угла β:
Умножение вектора на j является операцией его поворота в сторону опережения на 90о (против часовой стрелки) по отношению к исходному вектору, умножение на (- j) – соответственно поворот его на 90о в сторону отставания. Умножение вектора на -1(смена знака) означает его поворот на 180о в любом направлении поворота. Два комплексных числа, имеющие равные модули и равные, но противоположные по знаку аргументы, называют комплексно сопряжёнными числами. Если исходное комплексное число Свойства комплексно сопряжённых чисел:
Re(
Если Выражение
где Найдем мнимую часть комплексной функции времени для напряжения.
Мгновенное синусоидальное напряжение (ток, напряжение, ЭДС) является мнимой частью соответствующей комплексной функции времени. Таким образом, синусоидальные функции времени могут быть представлены векторами в комплексной плоскости, вращающимися против часовой стрелки с постоянной угловой скоростью ω, проекции которых на мнимую ось изменяются по синусоидальному закону.
Для единообразия принято на комплексной плоскости изображать вектора синусоидально изменяющихся во времени величин для момента времени При расчетах цепей, вместо комплексных амплитуд токов и напряжений, используют комплексные действующие значения, которые в
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 500; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.112.15 (0.007 с.) |

 . (2.1)
. (2.1) называют фазой. Величину φ, равную фазе в момент времени t = 0, называют начальной фазой. Фаза измеряется в радианах или градусах. Величину
называют фазой. Величину φ, равную фазе в момент времени t = 0, называют начальной фазой. Фаза измеряется в радианах или градусах. Величину  , обратную периоду, называют частотой. Частота f измеряется в герцах.
, обратную периоду, называют частотой. Частота f измеряется в герцах. . (2.2)
. (2.2) ,
,  ,
,  .
. (2.3)
(2.3) (2.4)
(2.4) . Известно, что проекция отрезка, вращающегося вокруг оси с постоянной угловой скоростью, на любую линию, проведенную в плоскости вращения, изменяется по синусоидальному закону.
. Известно, что проекция отрезка, вращающегося вокруг оси с постоянной угловой скоростью, на любую линию, проведенную в плоскости вращения, изменяется по синусоидальному закону. . Когда отрезок повернется на угол α1, проекция его
. Когда отрезок повернется на угол α1, проекция его  . Откладывая углы α1, α2,.. на горизонтальной оси, а проекции отрезка прямой - на вертикальной оси, получим ряд точек синусоиды (рис. 2.1).
. Откладывая углы α1, α2,.. на горизонтальной оси, а проекции отрезка прямой - на вертикальной оси, получим ряд точек синусоиды (рис. 2.1). и
и .
. .
.

 ,
, ) – действительная часть; b=Im (
) – действительная часть; b=Im ( .
. ;
; ;
; 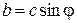 .
. ; φ=arctg
; φ=arctg  .
.
 .
.


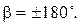
 ,
, 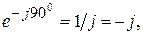

 , то комплексно сопряжённым числом будет
, то комплексно сопряжённым числом будет  .
.
 ;
;  )=(
)=( )/2, Im (
)/2, Im ( )/2 j.
)/2 j. , то вектор, умноженный на
, то вектор, умноженный на  , превратится во вращающийся со скоростью ωрадиус-вектор.
, превратится во вращающийся со скоростью ωрадиус-вектор. является комплексной функцией времени. Применительно к синусоидальным напряжениям и токам получим их комплексные функции времени:
является комплексной функцией времени. Применительно к синусоидальным напряжениям и токам получим их комплексные функции времени: ,
,  , (2.5)
, (2.5) ,
,  - комплексные амплитуды напряжения и тока (исходное положение векторов в комплексной плоскости).
- комплексные амплитуды напряжения и тока (исходное положение векторов в комплексной плоскости).
 .
. раз меньше. Совокупность векторов на комплексной плоскости, изображающих синусоидальные напряжения, токи и ЭДС одинаковой частоты, называют векторной диаграммой.
раз меньше. Совокупность векторов на комплексной плоскости, изображающих синусоидальные напряжения, токи и ЭДС одинаковой частоты, называют векторной диаграммой.


