
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы Ома, Кирхгофа и закон сохранения энергииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка. Пусть имеется некоторый участок цепи (рис. 1.7), крайние точки которого обозначены буквами а и b. Пусть ток I течет от точки а к точке b (от более высокого потенциала к более низкому). Следовательно, потенциал точки а( φ a) выше потенциала точки b( φ b) на значение, равное произведению тока I на сопротивление R: φ a =φb+ IR.
Рис. 1.7 В соответствии с определением напряжение между точками а и b Uab= φ a- φ b. Следовательно, Uab=IR, т.е. напряжение на сопротивлении равно произведению тока, протекающего по сопротивлению, на значение этого сопротивления. В электротехнике разность потенциалов на концах сопротивления принято называть либо напряжением на сопротивлении, либо падением напряжения. Положительное направление падения напряжения на каком-либо участке (направление отсчета этого напряжения), указываемое на рисунках стрелкой, совпадает с положительным направлением отсчета тока, протекающего по данному сопротивлению. Рассмотрим вопрос о напряжении на участке цепи, содержащей кроме сопротивления R, ЭДС Е (рис. 1.8, а, б). Найдем разность потенциалов (напряжение) между точками а и с для этих участков. По определению Uaс= φ a- φ с. Выразим потенциал точки а через потенциал точки с. При перемещении от точки с к точке b встречно направлению ЭДС Е (см. рис. 1.8, а) потенциал точки b оказывается меньше, чем потенциал точки с, на значение ЭДС Е: φ b= φ c-E. При перемещении от точки с к точке b согласно направлению ЭДС Е (рис.1.8, б) потенциал точки b больше, чем потенциал точки с,на значение ЭДС: φ b= φ c+E. Так как ток течет от более высокого потенциала к более низкому, в обеих схемах потенциал точки а выше потенциала точки b на величину падения напряжения на сопротивлении R:φ а= φ b+IR.
а) б) Рис. 1.8
Таким образом, для рис. 1.8, а:
для рис. 1.8, б:
Положительное направление напряжения Uaс показывают стрелкой от а к с. Согласно определению, Uса= φ с- φ а, поэтому Uас=-Uса, т.е. изменение чередования индексов равносильно изменению знака этого напряжения. Следовательно, напряжение может быть как положительной величиной, так и отрицательной. Закон Ома для участка цепи, не содержащего ЭДС Е, устанавливает связь между током и напряжением на этом участке. Применительно к рис.1.7
Закон Ома для участка цепи, содержащего источник ЭДС Е, позволяет найти ток этого участка по известной разности потенциалов ( φ a- φ с) на концах этого участка цепи и имеющейся на участке ЭДС Е. Так, из уравнения (1.1) для схемы рис.1.8, а следует
Из уравнения (1.2) для схемы рис.1.8, б следует:
В общем случае
Все электрические цепи подчиняются первому и второму законам Кирхгофа. Первый закон Кирхгофа можно сформулировать двояко: 1) алгебраическая сумма токов, подтекающих к какому-либо узлу схемы, равна нулю; 2) сумма подтекающих клюбому узлу токов равна сумме утекающихот этого узла токов.
Рис. 1.9 Применительно к рис.1.9, если подтекающие токи к узлу считать положительными, а вытекающие - отрицательными, то согласно первой формулировке I 1 -I 2 -I 3 -I 4 = 0; согласно второй I 1 =I 2 +I 3 +I 4. Физически первый закон Кирхгофа означает, что движение электрических зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются. В противном случае изменялись бы потенциалы узлов и токи в ветвях. Второй закон Кирхгофа также можно сформулироватьдвояко: 1) алгебраическая сумма падений напряженияв любом замкнутом контуре равна алгебраической сумме ЭДС, входящих в данный контур:
где m - число резистивных элементов; п – число ЭДС в контуре (в каждую из сумм соответствующие слагаемые входят со знаком плюс, если они совпадают с направлением обхода контура, и со знаком минус, если они не совпадают с ним); 2) алгебраическая сумма напряжений вдоль любого замкнутого контура
где т - число элементов контура. Второй закон Кирхгофа является следствием равенства нулю циркуляции вектора напряженности электрического поля вдоль любого замкнутого контура в безвихревом поле. Законы Кирхгофа справедливы длялинейных и нелинейных цепей при любом характере изменения во времени токов и напряжений. При протекании токов по сопротивлениям в них выделяется теплота. На основании закона сохранения энергии количество теплоты, выделяющееся в единицу времени в сопротивлениях цепи, должно равняться энергии, доставляемой за то же время источником питания. Если направление тока I, протекающего через источник ЭДС E, совпадает с направлением ЭДС, то источник ЭДС доставляет в цепь энергию в единицу времени, равную EI, и произведение ЕI входит в уравнение энергетического баланса с положительным знаком. Если же направление тока I встречно ЭДС Е, то источник ЭДС не поставляет энергию, а потребляет ее (например, заряжается аккумулятор), и произведение ЕI войдет в уравнение энергетического баланса с отрицательным знаком. Уравнение энергетического баланса при питании только от источников ЭДС имеет вид
В случае питания электрической цепи не только источниками ЭДС, но и источниками тока, при составлении уравнения энергетического баланса необходимо учесть и энергию, доставляемую источниками тока. Предположим, что к узлу а схемы подтекает ток J от источника тока, а от узла b этот ток утекает. Доставляемая источником тока мощность равна UаbJ. Общий вид уравнения энергетического баланса:
1.4. Эквивалентные преобразования пассивных участков электрической цепи При наличии в цепи только одного источника энергии в большинстве случаев цепь можно рассматривать как смешанное соединение источника и приемников энергии, т.е. нескольких резисторов, соединенных между собой параллельно, включенных последовательно с другими сопротивлениями (рис.1.10). Расчет смешанного соединения целесообразно начинать с определения эквивалентной проводимости параллельного соединения, а на основании этой проводимости легко найти обратную величину - эквивалентное сопротивление разветвления R. Для схемы, приведенной на рис. 1.10, а:
После замены разветвления эквивалентным сопротивлением (рис. 1.10, б) цепь можно рассчитывать как последовательное соединение; ток в неразветвленной части цепи:
а) б) Рис. 1.10
В ряде случаев расчет сложной схемы, состоящей из линейных сопротивлений, существенно упрощается, если в этой схеме заменить группу сопротивлений другой эквивалентной группой, в которой сопротивления соединены иначе, чем в замещаемой группе. Взаимная эквивалентность двух групп сопротивлений выразится в том, что после замены электрические условия во всей остальной схеме не изменятся. Рассмотрим преобразование звезды в треугольник и треугольника в звезду. Соединение трех сопротивлений, имеющих вид трехлучевой звезды, называют звездой (рис. 1.11), а соединение трех сопротивлений так, что они образуют собой стороны треугольника, - треугольником (рис.1.12). Обозначим токи, подтекающие к узлам 1, 2, 3, через I 1, I 2 и I 3. Выведем формулы преобразования. С этой целью выразим токи I 1, I 2 и I 3 в звезде и в треугольнике через разности потенциалов точек и соответствующие проводимости.
Рис. 1.11
Для звезды:
гдеφ о, φ 1, φ 2, φ 3 -потенциалы в точках 0, 1, 2, 3 соответственно. Подставим (1.10) в (1.9) и найдем φ 0:
Откуда
Подставим jо в выражение (1.10) для тока I 1:
С другой стороны, для треугольника в соответствии с обозначениями на рис. 1.12
Рис.1.12
Так как ток I 1 в схеме рис. 1.11 равен току I 1 в схеме рис. 1.12 при любых значениях потенциалов j1, j2 и j3, то коэффициент при j2 в правой части формулы (1.13) равен коэффициенту при j2 в правой части уравнения (1.12), а коэффициент при j3 в правой части формулы (1.13) равен коэффициенту при j3 в правой части уравнения (1.12). Следовательно,
Аналогично
Формулы (1.14), (1.15) дают возможность определить проводимости сторон треугольника через проводимости лучей звезды. Из уравнений (1.14)—(1.16) выразим сопротивления лучей звезды
С этой целью запишем дроби, обратные уравнениям (1.14)-(1.16):
где
Подставив формулы (1.17), (1.19) и (1.20) в выражение (1.18), получим
Следовательно,
Подставив m в выражение (1.19), найдем
Аналогично:
Структура формул (1.21)—(1.23) аналогична структуре формул (1.14) -(1.16).
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1065; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.144.162 (0.009 с.) |




 (1.1)
(1.1) (1.2)
(1.2) или
или  . (1.3)
. (1.3) .
. .
. . (1.4)
. (1.4)
 , (1.5)
, (1.5) , (1.6)
, (1.6) . (1.7)
. (1.7) . (1.8)
. (1.8)





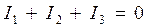 , (1.9)
, (1.9) ;
; 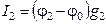 ;
;  , (1.10)
, (1.10) .
. . (1.11)
. (1.11) . (1.12)
. (1.12) . (1.13)
. (1.13)
 (1.14)
(1.14) . (1.15)
. (1.15)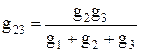 . (1.16)
. (1.16) ;
;  ;
;  через сопротивления сторон треугольника:
через сопротивления сторон треугольника: ;
;  ;
;  .
. ; (1.17)
; (1.17) , (1.18)
, (1.18) ; (1.19)
; (1.19) . (1.20)
. (1.20) .
. .
. . (1.21)
. (1.21) ; (1.22)
; (1.22) . (1.23)
. (1.23)


