
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип и метод наложения (суперпозици)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Чтобы составить общее выражение для тока в k -ветви сложной схемы, составим уравнения по методу контурных токов, выбрав контуры так, чтобы k -ветвь входила только в один k -контур. Тогда, согласно (1.27), ток в k -ветви равен контурному току Ikk:
Каждое слагаемое представляет собой ток, вызванный в k -ветви соответствующей контурной ЭДС. Каждую из контурных ЭДС можно выразить через ЭДС ветвей Е 1 , Е 2 ,..., Еn, затем сгруппировать коэффициенты при этих ЭДС и получить выражение следующего вида:
Если контуры выбраны таким образом, что какая-либо из ЭДС, например Еm, входит только в один m -контур, а в другие контуры не входит, то gkm =∆ km /∆. Уравнение (1.35) выражает собой принцип наложения, который формулируется следующим образом: ток в k -ветви равен алгебраической сумме токов, вызываемых каждой из ЭДС схемы в отдельности. Этот принцип справедлив для всех линейных электрических цепей. Принцип наложения положен в основу методу расчета, получившего название метода наложения. При расчете цепей по методу наложения поступают следующим образом: поочередно рассчитывают токи, возникающие от действия каждой из ЭДС, мысленно удаляя остальные из схемы, но оставляя в схеме внутренние сопротивления источников, и затем находят токи в ветвях путем алгебраического сложения этих частичных токов. Метод эквивалентного генератора При исследовании процессов в сложных цепях часто интересуются током, напряжением и мощностью только одной ветви. Отдельные ветви могут быть выделены из сложной цепи не только для исследования процессов именно в этих ветвях, но и для установления связи, например, между одной частью цепи с источником электрической энергии и другой - с приемниками. Во всех этих случаях выделяют ветвь, присоединенную к сложной цепи в двух точках (двумя зажимами). Часть электрической цепи произвольной конфигурации с двумя выделенными зажимами, именуемыми полюсами, называется двухполюсником. Двухполюсники, содержащие источники электрической энергии, называются активными, а двухполюсники, не содержащие источников электрической энергии, - пассивными. Всякий пассивный двухполюсник является потребителем электрической энергии и характеризуется одной величиной - сопротивлением R вн. Поэтому на эквивалентной схеме пассивный двухполюсник может быть представлен одним элементом - сопротивлением R вн, называемым внутренним или входным сопротивлением пассивного двухполюсника. Если известна схема пассивного двухполюсника, то для определения входного сопротивления нужно тем или иным способом ее «свернуть» относительно двух заданных зажимов. Рассмотрим, например, схему на рис. 1.19. Если выделить в этой схеме ветвь с источником ЭДС Е 1 и сопротивлением R 1, то остальную часть схемы (обведенную пунктиром) можно рассматривать относительно зажимов 1 – 1` как пассивный двухполюсник, а левую часть с источником ЭДС Е 1 и сопротивлением R 1 можно рассматривать как активный двухполюсник.
Рис. 1.19 В дальнейшем активные двухполюсники (рис. 1.20, а) будем обозначать прямоугольником с буквой А, а пассивные (рис. 1.20, б) - прямоугольниками с буквой П или без буквы П (просто прямоугольником).
а) б) Рис. 1.20 По отношению к выделенной ветви двухполюсник можно заменить эквивалентным генератором, ЭДС которого равна напряжению холостого хода на зажимах выделенной ветви, а внутреннее сопротивление равно входному сопротивлению двухполюсника. Пусть задана некоторая схема и требуется найти ток в одной ее ветви. Мысленно заключим всю схему, содержащую ЭДС и сопротивления, в прямоугольник, выделив из нее ветвь ab, в которой требуется найти ток I (рис.1.21, а). Ток I не изменится, если в ветвь ab включить две равные и противоположно направленные ЭДС: Е 1 и Е 2 (рис.1.21, б). На основании принципа наложения ток можно представить в виде суммы двух токов: I = I ' + I ''. Под током I будем понимать ток, вызываемый источником ЭДС Е 1 и всеми источниками ЭДС и тока активного двухполюсника, заключенными в прямоугольник. Ток I вызывается только одним источником ЭДС Е 2. В соответствии с этим для нахождения токов I ' и I '' используем схемы рис.1.21, в, г. В прямоугольнике П (рис.1.21, г) отсутствуют все источники, но оставлены их внутренние сопротивления.
а) б)
в) г) Рис. 1.21 Электродвижущая сила Е 1, направлена встречно напряжению Uab. По закону Ома для участка цепи, содержащего ЭДС,
Выберем Е 1 так, чтобы ток I ' был равен нулю. Отсутствие тока в ветви ab эквивалентно ее размыканию (холостому ходу). Напряжение на зажимах ab при холостом ходе ветви обозначим Uabx. Следовательно, если выбрать Е 1 = Uabx, то в соответствии с (1.36) I '= 0. Так как I = I '+ I '', а I '= 0, то I = I ''. Но ток I '' в соответствии со схемой (рис. 1.21, г) определяется как
где R вx - входное сопротивление двухполюсника по отношению к зажимам ab; R - сопротивление ветви аb. Уравнению (1.37) отвечает эквивалентная схема рис.1.22, а, где вместо двухполюсника изображены источник ЭДС UаЬx = Е 2 и сопротивление R вx.
а) б) Рис. 1.22 Совокупность источника ЭДС Е 2 = Uabx и сопротивления R вx можно рассматривать как некоторый эквивалентный генератор (R вх является его внутренним сопротивлением, а Uabx - его ЭДС). Таким образом, по отношению к выделенной ветви (ветви ab на рис.1.21, а) всю остальную часть схемы можно заменить эквивалентным генератором с перечисленными значениями параметров. Метод расчета тока в выделенной ветви, основанный на замене активного двухполюсника эквивалентным генератором, принято называть методом эквивалентного генератора (активного двухполюсника), а также методом холостого хода и короткого замыкания. Рекомендуется такая последовательность расчета тока этим а) найти напряжение на зажимах разомкнутой ветви ab; б) определить входное сопротивление R вx всей схемы по отношению к зажимам ab при закороченных источниках ЭДС и разомкнутых ветвях с источниками тока; в) подсчитать ток по формуле
Если сопротивление ветви a b равно нулю (R = 0), то для нее имеет место режим короткого замыкания, а протекающий по ней ток есть ток короткого замыкания (Ik). Из формулы (1.38) при R = 0
или
Из формулы (1.40) следует метод опытного определения входного сопротивления активного двухполюсника. Для этого необходимо измерить напряжение холостого хода на зажимах разомкнутой ветви U вх и ток короткого замыкания I к ветви. Заменив источник ЭДС источником тока, получим схему эквивалентного генератора, предоставленную на рис. 1.22, б.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 553; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.168.68 (0.007 с.) |

 . (1.34)
. (1.34) . (1.35)
. (1.35)





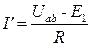 . (1.36)
. (1.36)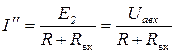 , (1.37)
, (1.37)
 . (1.38)
. (1.38) (1.39)
(1.39) . (1.40)
. (1.40)


