
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основанные на свойствах линейных цепейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для анализа и расчета разветвленных электрических цепей постоянного тока в п.1 рассмотрен ряд методов, позволяющих уменьшить порядок системы алгебраических уравнений по сравнению с методом непосредственного использования законов Кирхгофа. К ним относятся методы контурных токов, узловых потенциалов, двух узлов, эквивалентного генератора. Окончательные расчетные формулы этих методов получают в результате использования первого и второго законов Кирхгофа. Указанные законы в комплексной форме справедливы для цепей синусоидального тока (2.27)-(2.28). Поэтому в разветвленной электрической цепи, не имеющей элементов со взаимоиндуктивной связью, все расчетные уравнения для перечисленных методов (контурных токов, узловых потенциалов, двух узлов, эквивалентного генератора) справедливы для цепей синусоидального тока при условиях замены постоянных ЭДС, напряжений и токов (E, U, I) комплексами их действующих значений ( Расчет электрических цепей синусоидального тока при наличии в них элементов со взаимоиндуктивной связью имеет ряд особенностей и рассмотрен отдельно в п.2.7. Анализ линейных цепей не обязательно должен осуществляться с помощью таких общих методов расчета, как метод контурных токов или узловых потенциалов. Ниже будут рассмотрены методы, основанные на свойствах линейных электрических цепей и позволяющие при определенных постановках задач решить их более экономично. Метод наложения. Данный метод справедлив только для линейных электрических цепей и является особенно эффективным, когда требуется вычислить токи для различных значений ЭДС и токов источников при условии неизменности сопротивлений схемы. Данный метод основан на принципе наложения (суперпозиции), который формулируется следующим образом: ток в k– ветви линейной электрической цепи равен алгебраической сумме токов, вызываемых каждым из источников в отдельности. Аналитически принцип наложения для цепи, содержащей n источников ЭДС и m источников тока, выражается соотношением
где Доказательство принципа наложения можно осуществить на основе метода контурных токов. Решение системы уравнений, составленных по методу контурных токов, относительно любого контурного тока, например
где Каждая из ЭДС представляет собой алгебраическую сумму ЭДС в ветвях i –го контура. Если теперь все контурные ЭДС заменить алгебраическими суммами ЭДС в соответствующих ветвях, то после группировки слагаемых получится выражение для контурного тока Таким образом, при определении токов ветвей при помощи методаналоженияследует поочередно оставлять в схеме по одному источнику, заменяя остальные их внутренними сопротивлениями, и рассчитать составляющие искомых токов в этих схемах. После этого полученные результаты для соответствующих ветвей суммируются – это и будут искомые токи в ветвях исходной цепи. Принцип взаимности. Принцип взаимности формулируется следующим образом: для любой линейной цепи ток Из принципа взаимности следует равенство взаимных проводимостей Согласно принципу взаимности, если ЭДС
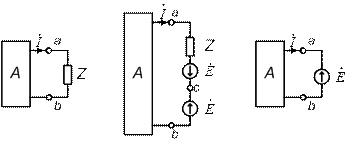
а) б) Рис.2.19 Принцип взаимности в сочетании с принципом наложения дает возможность существенно снизить трудоемкость расчета сложной цепи, в которой действует несколько источников ЭДС, особенно в том случае, если требуется определить ток в одной ветви этой цепи. Принцип компенсации. Принцип компенсации основан на теореме о компенсации, которая гласит: в любой электрической цепи без изменения токов в ее ветвях сопротивление в произвольной ветви можно заменить источником с ЭДС, численно равной падению напряжения на этом сопротивлении и действующей навстречу току в этой ветви. Для доказательства теоремы выделим из схемы произвольную ветвь с зажимами a,b и сопротивлением Z, по которой протекает ток
что позволяет гальванически соединить точки а и c, то есть перейти к цепи на рис. 2.20, в.
а) б) в)
Рис. 2.20
Второй вариант этой теоремы, согласно которому сопротивление в произвольной ветви можно заменить источником тока, ток которого численно равен току на этом сопротивлении и имеет то же направление, имеет аналогичное доказательство. Линейные соотношения в линейных электрических цепях. При изменении в линейной электрической цепи ЭДС (тока) одного из источников или сопротивления в какой-либо ветви токи в любой паре ветвей m и n будут связаны между собой линейным соотношением
где A и B – некоторые в общем случае комплексные константы. Действительно, согласно методу контурных токов, при изменении только одной ЭДС
а для тока в n – й ветви Здесь Умножив левую и правую части (2.45) на
Из теоремы компенсации известно, что любое сопротивление можно заменить источником ЭДС. Таким образом, линейное соотношение между двумя любыми токами (2.43) имеет место не только при изменении ЭДС, но и сопротивления в m –ветви.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 492; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.126.33 (0.009 с.) |

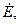
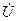 ,
,  ), проводимости и сопротивления (g, R) – комплексными проводимостями и сопротивлениями (Y, Z). При этом алгебраическая система уравнений заменяется системой комплексных уравнений.
), проводимости и сопротивления (g, R) – комплексными проводимостями и сопротивлениями (Y, Z). При этом алгебраическая система уравнений заменяется системой комплексных уравнений. ,
,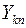 - комплекс входной проводимостиk – й ветви, численно равный отношению тока к ЭДС в этой ветви при равных нулю ЭДС в остальных ветвях;
- комплекс входной проводимостиk – й ветви, численно равный отношению тока к ЭДС в этой ветви при равных нулю ЭДС в остальных ветвях;  - комплекс взаимной проводимостиk – й и i – й ветвей, численно равный отношению тока в k – й ветви и ЭДС в i – й ветви при равных нулю ЭДС в остальных ветвях,
- комплекс взаимной проводимостиk – й и i – й ветвей, численно равный отношению тока в k – й ветви и ЭДС в i – й ветви при равных нулю ЭДС в остальных ветвях,  - коэффициент передачи тока, являющийся в отличие от проводимостей безразмерной величиной.
- коэффициент передачи тока, являющийся в отличие от проводимостей безразмерной величиной. , имеет вид:
, имеет вид: ,
, - определитель системы уравнений, составленных по методу контурных токов;
- определитель системы уравнений, составленных по методу контурных токов;  - алгебраическое дополнение определителя.
- алгебраическое дополнение определителя. в виде алгебраической суммы составляющих токов, вызванных каждой из ЭДС ветвей в отдельности. Поскольку систему независимых контуров всегда можно выбрать так, что рассматриваемая ветвь войдет только в один контур, то принцип наложения справедлив для токов любых ветвей.
в виде алгебраической суммы составляющих токов, вызванных каждой из ЭДС ветвей в отдельности. Поскольку систему независимых контуров всегда можно выбрать так, что рассматриваемая ветвь войдет только в один контур, то принцип наложения справедлив для токов любых ветвей. в k- ветви, вызванный источником ЭДС
в k- ветви, вызванный источником ЭДС  , находящемся в m- ветви,
, находящемся в m- ветви,  , равен току
, равен току  в m- ветви, вызванному источником ЭДС
в m- ветви, вызванному источником ЭДС  ( численно равной ЭДС
( численно равной ЭДС 

 .
. (рис. 2.19, б).
(рис. 2.19, б).
 , а всю остальную часть схемы условно обозначим некоторым активным двухполюсником А
, а всю остальную часть схемы условно обозначим некоторым активным двухполюсником А  (рис. 2.20, б) режим работы цепи не изменится. Для этой цепи
(рис. 2.20, б) режим работы цепи не изменится. Для этой цепи
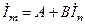 , (2.43)
, (2.43) в k –ветви выражение для тока в m –ветви можно записать в компактном виде:
в k –ветви выражение для тока в m –ветви можно записать в компактном виде: ; (2.44)
; (2.44) . (2.45)
. (2.45) и
и  - составляющие токов соответственно в m и n -ветвях, обусловленные всеми остальными источниками, кроме
- составляющие токов соответственно в m и n -ветвях, обусловленные всеми остальными источниками, кроме  , вычтем полученное соотношение из уравнения (2.44). В результате получим линейное соотношение, аналогичное (2.43):
, вычтем полученное соотношение из уравнения (2.44). В результате получим линейное соотношение, аналогичное (2.43): .
.


