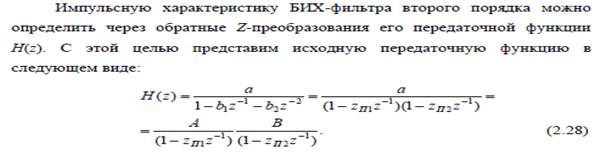Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
постановка и решения задачи аппроксимации в классе БИХ-цепей.Содержание книги
Поиск на нашем сайте
Требуется найти минимальный порядок D-мерного вектора (D=M+L+2) весовых коэффициентов
где p (ω) – весовая функция, εдоп – допустимое отклонение воспроизводимой функции передачи от желаемой. Воспроизводимая функция передачи HB (j, Решение: Поиск оптимального решения по критерию (2.13) может выполняться методами машинной аппроксимации. Однако такой подход не даѐт чѐтко обозначенной методики поиска, и, как правило, используется метод перебора. Поэтому оптимальное решение можно найти для сравнительно малых значений M и L при малоразрядном квантовании коэффициентов. На практике нашли место косвенные методы расчѐта БИХ-фильтров частотной селекции. Идея метода заключается в использовании хорошо разработанной методики синтеза аналоговых фильтров с последующим использованием билинейного преобразования для перехода H (p) Отметим, что билинейное преобразование является нелинейным и это приводит к нелинейному преобразованию частот. Надо взять частоты среза fc1, fc2 таким образом, чтобы в процессе преобразования они попали в ту область частот, которая задаѐтся для характеристик цифрового фильтра.
17. Каноническая и каскадная форма БИХ фильтра. Пусть передаточная функция цифрового фильтра
Используя обратное Z- преобразование, получим прямую форму реализации БИХ-цепи M -го порядка
Графическое отображение прямой формы реализации представим в виде (рис. 2.17)
Рис. 2.17. Прямая форма БИХ-фильтра M-го порядка. Заметим, что верхняя половина реализует нули передаточной функции (2.14), а нижняя половина еѐ полюсы. Отметим также, что эти фильтры, формирующие нули и полюсы, соединены последовательно, где V (n) – реакция первого фильтра, y (n) – окончательная реакция на выходе второго фильтра. Меняя порядок суммирования нулей и полюсов, получим (рис. 2.18):
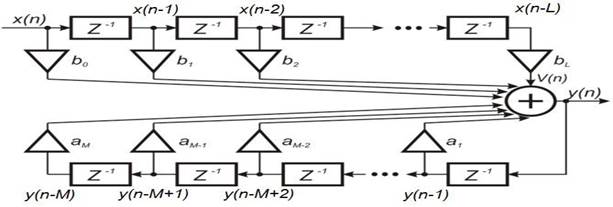
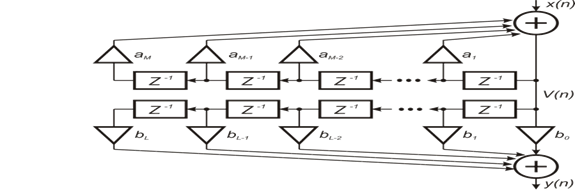
Рис. 2.18. Переход от прямой формы БИХ-фильтра к канонической. Исключив, лишнюю линию задержки для промежуточной переменной V (n), получим каноническую форму реализации БИХ-цепи (рис. 2.19).
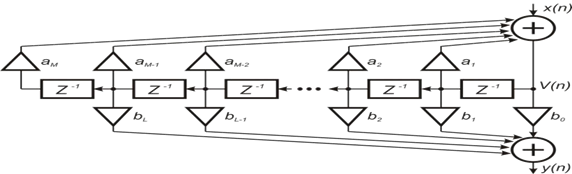
Рис. 2.19. Каноническая форма БИХ-фильтра. Отметим, что каноническая форма позволяет уменьшить ѐмкость памяти данных до двух раз. Однако прямая и каноническая формы используются на практике только для фильтров, порядок которых меньше пяти (M <5), т.к. с увеличением порядка M многократно увеличивается чувствительность частотных характеристик к неточному представлению коэффициентов, и встаѐт проблема их устойчивой работы.
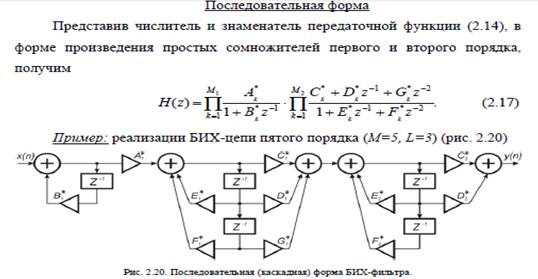
Последовательная форма реализации БИХ-цепи имеет следующие преимущества: • Значительное уменьшение чувствительности характеристик БИХ-цепи к неточному представлению коэффициентов. • Появляется возможность оптимизации порядка соединения фильтров 1го и 2-го порядков для минимизации уровня собственных шумов. • Открывается возможность простой многопроцессорной реализации цифрового фильтра, работающего в режиме реального времени на высокой частоте дискретизации. 18. Разностное уравнение цифрового фильтра в классе БИХ цепей. В классе БИХ-цепей вход x (n) и выход y (n) связаны друг с другом разностным уравнением вида:
где ak и bl – постоянные коэффициенты. Приняв a0 =1 и перенеся все составляющие выходного сигнала, кроме текущего y (n), в правую часть, получим:
Отметим, что в соответствии с прямой формой реализации (2.10) можно вычислить текущее значение y (n) по входному значению x (n), извлекая из памяти данных L предшествующих отсчѐтов входного сигнала x (n-l) и M отсчѐтов выходного сигнала y (n-k). Встаѐт вопрос: как установить связь между множеством коэффициентов (ak, bl) и пространством строго воспроизводимых функций передачи Hв (jω). Применяя Z- преобразование к обеим частям уравнения (2.9), получим
Используя подстановки вида m=n-k, r=n-l и меняя порядок суммирования, получим Тогда
Выполнив подстановку z =
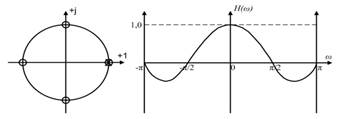
19. Передаточная функция и импульсная характеристика цепи 2-ого порядка.
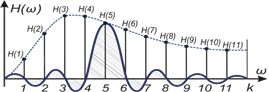
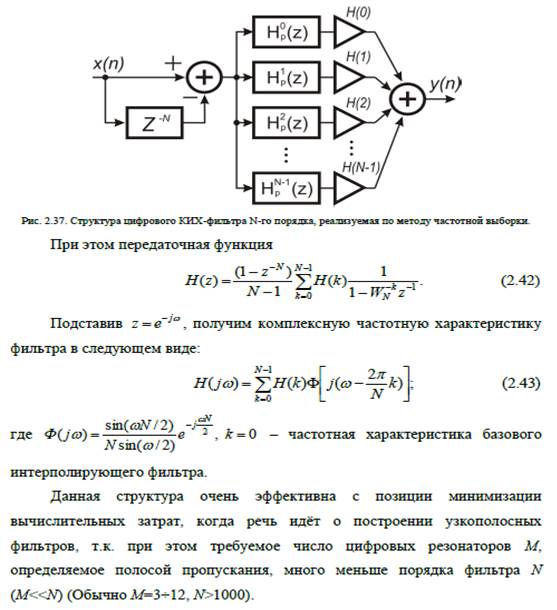
20. Метод частотной выборки и его модификация. Пусть необходимо реализовать фильтр со следующей частотной характеристикой (рис. 2.35):
Рис. 2.35. Желаемая частотная характеристика фильтра. Анализ представленного рисунка показывает, что любая желаемая частотная характеристика H (ω) может быть воспроизведена с любой априорно заданной точностью путѐм параллельного соединения интерполирующих фильтров с частотной характеристикой, близкой к функции sin (ω) /ω,и последующей весовой обработкой с использованием
22. Дискретное преобразование Фурье и его свойства
23. Алгоритм быстрого преобразования Фурье и его эффективность.
24. Математическое описание ЦФ в классе КИХ и БИХ цепей сравнительный анализ. Эффективность линейных ЦЦ.
БИХ-цепи имеет следующие преимущества: • Значительное уменьшение чувствительности характеристик БИХ-цепи к неточному представлению коэффициентов. • Появляется возможность оптимизации порядка соединения фильтров 1го и 2-го порядков для минимизации уровня собственных шумов. • Открывается возможность простой многопроцессорной реализации цифрового фильтра, работающего в режиме реального времени на высокой частоте дискретизации.
25. Вычисление быстрой свертки на основе БПФ.
26. Математическая формализация и решения задач оптимального проектирования ЦФ.
27. Прямая и обратная задача оптимального проектирования ЦФ.
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 398; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.95.167 (0.007 с.) |

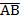 (a 0, a 1, a 2,..., aM , b 0, b 1, b 2,..., bL) и сам вектор, такие, что имеет место неравенство вида
(a 0, a 1, a 2,..., aM , b 0, b 1, b 2,..., bL) и сам вектор, такие, что имеет место неравенство вида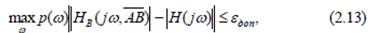
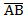 ) может быть найдена из выражения (2.12).
) может быть найдена из выражения (2.12).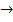 H (z).
H (z).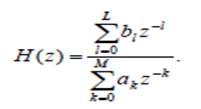
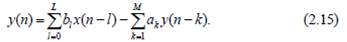

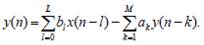
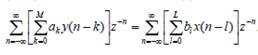

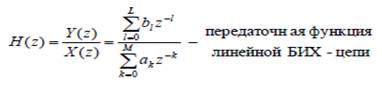
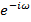 в выражение (2.11), получим функцию передачи БИХ-цепи
в выражение (2.11), получим функцию передачи БИХ-цепи