
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
КИХ-фильтры с оконным ФЧХ. Синтез КИХ-фильтра оконным методомСодержание книги
Поиск на нашем сайте
Для ЦЦ с линейной ФЧХ импульсная характеристика h(n) является симметричной, т.е. выполняется условие вида Эффект колебаний Гиббса Если желаемая частотная характеристика имеет прямоугольный вид, то воспроизводимая частотная характеристика реализуемого фильтра получается как свѐртка в частотной области прямоугольной ЧХ H(ω) и спектрального окна W(ω) вида sin(ω)/ω, соответствующего прямоугольной весовой функции W(n) (рис. 2.10 и рис. 2.11)
Заметим, что уровень боковых лепестков в зоне непрозрачности достигает 13 дБ по первому лепестку. При этом, если увеличить длину прямоугольного окна, то пропорционально увеличивается частота колебаний и сужается переходная зона АЧХ. Но при этом первый лепесток в зоне непрозрачности лежит на уровне 13 дБ. Решение задачи аппроксимации опирается на один из двух подходов: оконные методы (не оптимальное решение); минимаксная аппроксимация (с использованием численных методов оптимизации).
1. Окно Бартлета (треугольное) (рис. 2.12)
Позволяет уменьшить уровень колебаний Гиббса на 25 дБ, но сопровождается уменьшением показателя прямоугольности АЧХ в 2 раза. 2. Окно Хэннинга («косинус на пьедестале») (рис. 2.13)
При той же эффективной ширине полосы пропускания, что и у треугольного окна, позволяет уменьшить уровень колебаний Гиббса до 31 дБ. 3. Окно Хэмминга Близкое по форме к «косинусу на пьедестале», но позволяющее уменьшить уровень колебаний Гиббса до 41 дБ. Однако, не обеспечивает столь быстрого ослабления боковых лепестков с увеличением частоты, которое имеет место для прямоугольного и треугольного окон. Все эти окна не дают оптимального решения, т.е. не обеспечивают минимального уровня боковых лепестков при заданной ширине переходной зоны АЧХ. Представление с наперед заданной точностью желаемой частотной характеристики H(ω), не принадлежащей пространству функций RN, имеет место для всех функций H(ω), отвечающих условиям теоремы Вейерштрасса.
10. Z-преобразование и его свойства Пусть x(n) – некоторая временная последовательность, в общем случае заданная при всех Z-преобразование, где z – комплексная переменная. X(z) – Z-образ последовательности x(n). Имеет место обратное Z-преобразование
Свойства Z-преобразований
Установим связь между Z-образом выходного сигнала Используя Отсюда следует
Таким образом, получим: Здесь H(z) определяет преобразование Z-образа X(z) входного сигнала при его прохождении через цифровую цепь. H(z) называют передаточной или системной функцией цепи. Установлено, что между передаточной функцией H(z) и комплексной частотной характеристикой H(jω) имеет место простая связь.
11. Преобразование Фурье и его связь с Z-преобразованием.
Z-преобразование, где z – комплексная переменная. X(z) – Z-образ последовательности x(n). Здесь забить формулы связи зет с преобразованием Фурье.
Проблемы устойчивости и чувствительности цифровых БИХ-фильтров. Вследствие обратной связи требуется очень точное представление коэффициентов БИХ-фильтра. Все полюсы должны находиться в окружности единичного радиуса. Проблемой устойчивости является близость полюсов к единичной окружности. Чувствительность полюсов и цифровых БИХ-фильтров многократно возрастает с увеличением порядка фильтра, так как количественная оценка чувствительности полюсов к неточному представлению коэффициентов обратно пропорциональна произведению расстояния между ними.
Описание линейных дискретных систем в Z-области.
Передаточная функция цифровой цепи. Взаимосвязь между передаточной функцией и разностным уравнением.
15. Передаточные функции и импульсные характеристики цифровые звенья первого порядка.
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 734; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.84 (0.008 с.) |

 Если учесть это в (2.5), приходим к выражению вида
Если учесть это в (2.5), приходим к выражению вида  - тригонометрический полином.
- тригонометрический полином.


 Тогда преобразование вида
Тогда преобразование вида 


 , Z-образом входного сигнала
, Z-образом входного сигнала  и Z-образом импульсной характеристики
и Z-образом импульсной характеристики  . Найдѐм Z-преобразование левой и правой части свѐртки, используя свойства линейности и задержки, установленные выше.
. Найдѐм Z-преобразование левой и правой части свѐртки, используя свойства линейности и задержки, установленные выше. 
 и меняя порядок суммирования, получим
и меняя порядок суммирования, получим 
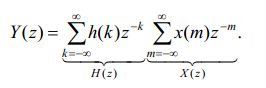

 Таким образом, выполнив подстановку вида
Таким образом, выполнив подстановку вида  , получим:
, получим:










