
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схема звезда-звезда без нулевого проводаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Трехфазная цепь по данной схеме рассчитывается методом двух узлов. При любой несимметричной нагрузке между нейтральными точками источника и нагрузки возникает напряжение смещения нейтрали, определяемое по формуле
Фазные напряжения нагрузки определяются по (3.6) и образуют несимметричную трехфазную систему. Фазные токи определяются по (3.7) и образуют также несимметричную трехфазную систему. Рассмотрим наиболее характерные несимметричные режимы обрыва и короткого замыкания одной из фаз нагрузки. Будем считать, что данные режимы возникают при начальной симметричной нагрузке фаз При обрыве фазы А
Векторная диаграмма режима приведена на рис.3.7. Нейтральная точка нагрузки
Рис.3.7 Рис. 3.8 Трехфазная система фазных напряжений нагрузки несимметрична:
Модули фазных напряжений Трехфазная система фазных токов также несимметрична:
При коротком замыкании фазы А нейтральная точка нагрузки
В режиме короткого замыкания одной фазы величины фазных напряжений неповрежденных фаз B, C возрастают до величины линейных напряжений, т.е. в 1.73 раза, что нарушает нормальное функционирование электроприемников.
Соединение нагрузки треугольником Трехфазная система напряжений нагрузки симметрична и определяется симметричной системой линейных ЭДС источника (рис.3.4). Фазные и линейные напряжения одинаковы U л = U ф. Фазные токи не связаны друг с другом и зависят только от соответствующих сопротивлений фаз. При неравномерной нагрузке фаз трехфазная система фазных токов несимметрична и определяется следующими уравнениями:
Трехфазная система линейных токов несимметрична и определяется (3.4). Например, если в трехфазной цепи, соединенной треугольником, при симметричной активной нагрузке (векторная диаграмма – рис.3.5) произойдет обрыв провода в фазе AB, трехфазные системы фазных и линейных токов имеют вид:
Активная, реактивная и полная мощности трехфазной системы
Cумма активных мощностей фаз нагрузки и активной мощности в сопротивлении, включенном в нулевой провод, определяет активную мощность трехфазной системы:
Cумма реактивных мощностей фаз нагрузки и реактивной мощности в сопротивлении, включенном в нулевой провод, определяет реактивную мощность трехфазной системы:
Полная мощность трехфазной системы определяется соотношением (2.34):
При неравномерной нагрузке фаз ( При равномерной нагрузке фаз (
где φ - угол между комплексами фазных напряжения При равномерной нагрузке для трехфазной системы имеют место соотношения между линейными и фазными напряжениями и токами: - для звезды - - для треугольника - На основании (3.12) для обоих способов соединения фаз получаем формулы для мощностей, выраженные через линейные напряжения и токи:
ПРАКТИЧЕСКАЯ ЧАСТЬ Раздел 1. Цепи постоянного тока
Задача 1.1 Определить
Задача 1.2 Определить Ответ:
Задача 1.3 Определить 1) Потенциалы узлов а и b равны. Сл. это Ответ:
Определить Ответ:
Задача 1.5 До коммутации ток в цепи 1А. Определить ток после коммутации ключа. Ответ: 1.5А
До коммутации ток в цепи 1А. Определить ток после коммутации ключа. Ответ: 3А
Определить Ответ:
Определить Ответ:
Определить 1) Ответ:
2. Потенциал точек а и b одинаков. Схему можно представить как Сопротивление ромба R. Сопротивление половины цепи вдоль cd 2R, следовательно
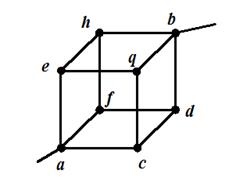
Задача 1.10 Сопротивление ребра куба R. Определить 1) RАВ; 2) RАС; 3) RAD
Решение: 1. Потенциалы точек c, f, e одинаковы – это одна точка, а точки h, q, d – другая точка
2. Точки одинакового потенциала c и f, точки q и d: 3. 4.
3. Точки f и c и точки n и q имеют равные потенциалы. Эквивалентная схема.
Узлы n, q и f, c имеют одинаковый потенциал сопротивление R/2 между ними можно не учитывать, так как ток через него не идет. Ответ: 1)
В левой схеме преобразуем треугольник в звезду В правой схеме преобразуем внешний треугольник в звезду. Точки О и О’ имеют одинаковый потенциал и могут быть соединены.
Отсюда общее сопротивление
Задача 1.12 E=17 В R1=R2=R3=R4=3 Ом R5=5 Ом
Решение: Преобразуем треугольник(1,2,3) в звезду(1,2,3)
В исходной схеме:
Баланс мощностей:
Задача 1.13 Определить
Ответ:
Определить токи в ветвях.
Решение: На основании законов Кирхгофа: В схеме 5 ветвей (b = 5) и 3 узла (y = 3) По (1 узел) (2 узел) По 2 закону Кирхгофа Обход контуров по часовой стрелке. (1 контур) (2 контур)
Ответ:
Задача 1.15 Определить токи в ветвях.
Решение: Применяем метод контурных токов. Независимых контуров два Уравнение цепи:
где
отсюда токи:
Произвольно выберем направление токов ветвей и найдем их.
Ответ:
Определить токи по М.У.Н.
Решение: Примем за опорный узел 3. Составим уравнение по М.У.Н.
откуда
Уравнение баланса мощности:
408 Вт = 408 Вт Ответ: Задача 1.17 Решить задачу №14 методом наложения С помощью закона Ома рассчитываем токи в цепи от действия каждого источника Токи от действия источника
Токи от действия источника
Токи от действия источника тока J
Токи исходной цепи:
Задача 1.18 Схема задачи №1.14. Определить ток первой ветви методом эквивалентного генератора Решение:
Для определения
Задача 1.19
Ответ: Баланс мощностей:
Источник
Определить токи Ответ:
Задача 1.21
Ответ: Задача 1.22
Ответ:
Задача 1.23 Определить токи 1. Методом двух узлов 2. Методом наложения Ответ:
Определить токи методом узловых напряжений Ответ:
Раздел 2. Основы символического метода
Задача 2.1 Написать комплекс действующего значения синусоидальной функции времени:
Решение: Модуль комплекса действующего значения совпадает с действующим значением синусоидальной величины, а аргумент совпадает с начальной фазой этой величины:
Решение:
Решение:
Задача 2.4 Написать комплекс действующего значения синусоидальной функции времени:
Решение: Отсюда
Решение:
Задача 2.6 Найти синусоидальную функции времени, изображенную комплексом действующего значения:
Решение:
Решение: (т.к.
Отсюда
Решение:
Отсюда
Задача 2.9 Найти синусоидальную функции времени, изображенную комплексом действующего значения:
Решение:
Отсюда
Задача 2.10 Найти синусоидальную функции времени, изображенную комплексом действующего значения:
Решение:
Отсюда
Задача 2.11 Найти синусоидальную функции времени, изображенную комплексом действующего значения:
Решение:
Отсюда
Задача 2.12 Найти синусоидальную функции времени, изображенную комплексом действующего значения:
Решение:
Отсюда
Задача 2.13 Определить сдвиг фаз
Задача 2.14 Определить комплексное сопротивление, если напряжение и ток равны:
Решение: На основании закона Ома
Задача 2.15 Определить мгновенное значение падения напряжения, если известны ток
Решение: На основании закона Ома
Отсюда
Задача 2.16 Определить мгновенное значение падения напряжения, если известны ток Решение: На основании закона Ома
Отсюда
Решение:
Решение: На основании первого закона Кирхгофа:
Отсюда
Задача 2.19 Определить проводимость Y, если известно комплексное сопротивление Решение: Отсюда Задача 2.20 Найти выражение для комплексного сопротивления Z и комплексной проводимости Y, если
Решение:
Задача 2.21 Найти выражение для комплексного сопротивления Z и комплексной проводимости Y, если
Решение:
Задача 2.22 Определить комплекс полной мощности, если Решение:
Задача 2.23 Определить активную и реактивную мощности, если Решение:
Отсюда Задача 2.24 Известны ток и напряжение:
Решение: где
Отсюда
Задача 2.25 Определить сопротивление схемы (R и L), если
Решение:
Отсюда
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 2138; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.123.149 (0.017 с.) |

 . (3.9)
. (3.9) активно-индуктивного характера.
активно-индуктивного характера. и из (3.9) получаем напряжение смещения нейтрали
и из (3.9) получаем напряжение смещения нейтрали .
. смещается на средину вектора линейного напряжения
смещается на средину вектора линейного напряжения  , величина напряжения смещения нейтрали составляет 0,5
, величина напряжения смещения нейтрали составляет 0,5  .
.


 .
. равны и составляют 0,866 U ф, а фазы их противоположны по знаку.
равны и составляют 0,866 U ф, а фазы их противоположны по знаку. ;
;  ;
;  .
. . Векторная диаграмма этого режима приведена на рис.3.8. Трехфазные системы фазных токов и напряжений несимметричны:
. Векторная диаграмма этого режима приведена на рис.3.8. Трехфазные системы фазных токов и напряжений несимметричны: ;
; 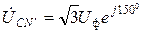 ;
; ;
;  ;
;  .
. ;
;  ;
;  .
.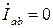 ;
;  ;
;  ;
;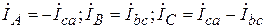 .
. . (3.10)
. (3.10) . (3.11)
. (3.11) .
. ) расчеты активной, реактивной и полной мощностей выполняются отдельно для каждой фазы по выражениям (2.34), (2.35).
) расчеты активной, реактивной и полной мощностей выполняются отдельно для каждой фазы по выражениям (2.34), (2.35). ) ток в нулевом проводе отсутствует, а во всех фазах величины фазных напряжений и токов одинаковы. Следовательно, из (3.10) и (3.11) получаем:
) ток в нулевом проводе отсутствует, а во всех фазах величины фазных напряжений и токов одинаковы. Следовательно, из (3.10) и (3.11) получаем: ;
;  ;
;  ;
; ;
; 
 ;
; , (3.12)
, (3.12) и тока
и тока  .
. ;
;  ,
, ;
;  .
. ;
;  ;
;  .
.

 Ответ:
Ответ: 

 Проверить преобразованием треугольника в звезду
Проверить преобразованием треугольника в звезду Задача 1.4
Задача 1.4

 Задача 1.6
Задача 1.6 Задача 1.7
Задача 1.7
 Задача 1.8
Задача 1.8
 Задача 1.9
Задача 1.9 2)
2)  Сопротивление каждой ветви R
Сопротивление каждой ветви R ,
, 
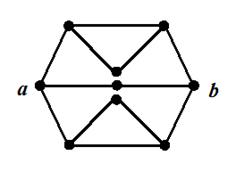 Решение:
Решение: 1. В силу симметрии ток в узле o отсутствует, т.е. эта точка есть точка равного потенциала
1. В силу симметрии ток в узле o отсутствует, т.е. эта точка есть точка равного потенциала



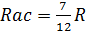


 .
. ; 2)
; 2)  ; 3)
; 3)  .
.
 Задача 1.11
Задача 1.11
 Решение: В левой схеме одинаковое сопротивление по 3 Ома. Определяем радиус правой схемы, чтобы они были эквивалентными.
Решение: В левой схеме одинаковое сопротивление по 3 Ома. Определяем радиус правой схемы, чтобы они были эквивалентными.




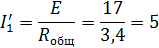



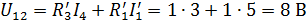









 .
. Ом
Ом Ом
Ом Ом
Ом Ом
Ом Ом
Ом Ом
Ом Ом
Ом Задача 1.14
Задача 1.14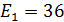 В
В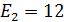 В
В А
А Ом
Ом Ом
Ом Ом
Ом уравнений
уравнений 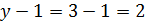
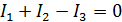




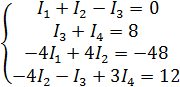
 А
А 
 А
А 

 А
А А
А

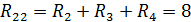 ;
;

 А
А А
А А
А А
А А
А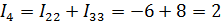 А
А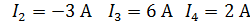
 Задача 1.16
Задача 1.16

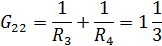




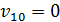
 В
В




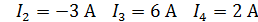
 :
:
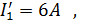

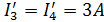
 :
:
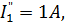




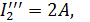

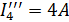




 Разрешаем цепь относительно первой ветви
Разрешаем цепь относительно первой ветви 
 определяем ток
определяем ток  методом контурных токов из уравнения
методом контурных токов из уравнения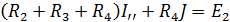 ,откуда
,откуда
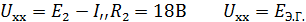





 Определить токи ветвей
Определить токи ветвей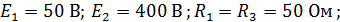





 Задача 1.20
Задача 1.20
 .
.
 Определить токи методом контурных токов
Определить токи методом контурных токов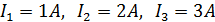 .
.
 Определить токи методом контурных токов
Определить токи методом контурных токов .
.
 и
и 

 Задача 1.24
Задача 1.24


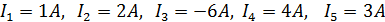 .
.
 , А.
, А. , А.
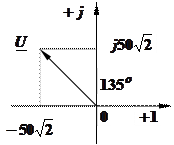
, А. Задача 2.2 Написать комплекс действующего значения синусоидальной функции времени:
Задача 2.2 Написать комплекс действующего значения синусоидальной функции времени:  , В.
, В.
 Задача 2.3 Написать комплекс действующего значения синусоидальной функции времени:
Задача 2.3 Написать комплекс действующего значения синусоидальной функции времени:  , B.
, B.
 , А.
, А. , А.
, А. , А.
, А. Задача 2.5 Написать комплекс действующего значения синусоидальной функции времени:
Задача 2.5 Написать комплекс действующего значения синусоидальной функции времени:  , В.
, В.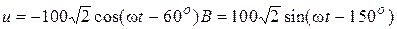 , B.
, B. 
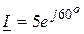 , A.
, A. , oтсюда
, oтсюда  , A.
, A. Задача 2.7 Найти синусоидальную функции времени, изображенную комплексом действующего значения:
Задача 2.7 Найти синусоидальную функции времени, изображенную комплексом действующего значения:  , A.
, A.
 ).
). , A.
, A. Задача 2.8 Найти синусоидальную функции времени, изображенную комплексом действующего значения:
Задача 2.8 Найти синусоидальную функции времени, изображенную комплексом действующего значения:  , A
, A , (т.к.
, (т.к.  ).
). , A.
, A. , В.
, В.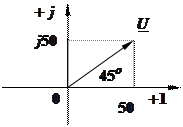

 , В.
, В. , В.
, В.

 , В.
, В. , В.
, В.
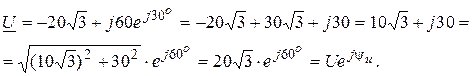
 , В.
, В. , В.
, В.

 между напряжением и током, комплексы действующих значений которых равны:
между напряжением и током, комплексы действующих значений которых равны:  , B,
, B,  , A.
, A. Решение:
Решение: , B,
, B,  ;
; , A,
, A,  ;
; .
.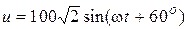 , В;
, В;  , А.
, А.
 В,
В,  , А;
, А; , Ом.
, Ом.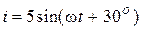 , А, и комплексное сопротивление
, А, и комплексное сопротивление  , Ом.
, Ом. ;
; , Ом,
, Ом,  , А;
, А; , В.
, В. , В.
, В. , А, и комплексное проводимость
, А, и комплексное проводимость 
 ;
; А,
А,  ;
; .
. , В.
, В. Задача 2.17 Найти сумму токов
Задача 2.17 Найти сумму токов  , мгновенные значения которых равны:
, мгновенные значения которых равны:  , А,
, А,  , А,
, А,  , А.
, А. ;
; , А.
, А. , А.
, А. , А.
, А. Отсюда
Отсюда  , А.
, А. Задача 2.18 Определить
Задача 2.18 Определить  , если известно:
, если известно: , А,
, А, , А,
, А, , А.
, А. ;
;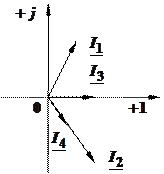
 , A;
, A; , A,
, A, 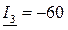 A;
A;
 , А.
, А. Ом.
Ом. ;
;  , Ом.
, Ом. .
. Oм,
Oм,  Гн,
Гн,  с-1
с-1 
 , Ом.
, Ом. .
. Oм,
Oм,  c-1,
c-1, 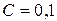 мкФ.
мкФ.

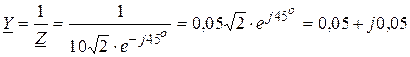 .
. , В,
, В,  , А.
, А. ;
; , В,
, В, 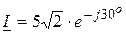 , А,
, А,  , А;
, А; .
. , В,
, В,  , В,
, В,  , А.
, А. ;
; , В,
, В,  , А,
, А,  , А;
, А; .
. , Вт,
, Вт,  , вар.
, вар. , А,
, А,  , В. Определить активную и реактивную мощности.
, В. Определить активную и реактивную мощности. ,
,  ,
, ;
;  , Вт;
, Вт;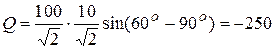 , вар.
, вар. , В,
, В, 
 , А.
, А. .
. ,
,  , Ом.
, Ом.


