
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы расчета линейных электрических цепейСодержание книги
Поиск на нашем сайте
Расчет цепей с использованием законов Кирхгофа Законы Кирхгофа используют для нахождения токов в ветвях схемы. Обозначим число всех ветвей схемы через b, число ветвей, содержащих источники тока, через b ИT, число узлов - у. В каждой ветви схемы течет свой ток. Так как токи в ветвях с источниками тока известны, то число неизвестных токов равняется (b - b ИT). Перед тем как составлять уравнения, необходимо произвольно выбрать: а) положительные направления токов в ветвях и обозначить их на схеме; б) положительные направления обхода контуров для составления уравнений по второму закону Кирхгофа. Чтобы получить линейно независимые уравнения, по первому закону Кирхгофа составляют число уравнений, равное числу узлов без единицы, т.е. у - 1. По второму закону Кирхгофа составляют число уравнений n, равное n= b - b ИT - (у - 1).
При записи линейно независимых уравнений по второму закону Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляются уравнения, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону Кирхгофа, т.е. число уравнений по второму закону Кирхгофа равно числу независимых контуров. Пример 1. Найти токи в ветвях схемы рис. 1.13, в которой Е 1 = 80 В, Е 2 = 64В, R 1= 6 Ом, R 2 = 4 Ом, R 3 = 3 Ом, R 4= 10 Ом.
Рис. 1.13 Решение. Произвольно выбираем положительные направления тока в ветвях. В схеме рис. 1.13 b =3; b ИТ=0; y =2. Следовательно, по первому закону Кирхгофа можно составить только одно уравнение y -1=1:
По второму закону Кирхгофа составим два уравнения. Положительные направления обхода контуров выбираем по часовой стрелке.
Для контура R 1 E 1 R 2 E 2
Знак плюс перед I 1 R 1 взят потому, что направление тока совпадает с направлением обхода контура, а знак минус перед I 2 R 2 потому, что направление I 2 встречно обходу контура. Для контура E 2 R 2 R 3 R 4:
Совместное решение трех уравнений дает I 1 = 14 A, I 2 = -15 A, I 3 = -1 A. В рассматриваемом примере отрицательными оказались токи I 2 и I 3, это следует понимать так, что в действительности токи I 2 и I 3 направлены в обратную сторону. Метод контурных токов При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют токи ветвей. Таким образом, метод контурных токов можно определить как метод расчета, в котором в качестве неизвестных принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, составляемых для схемы по второму закону Кирхгофа. Преимуществом этого метода, по сравнению с методом на основе законов Кирхгофа, является меньшая вычислительная работа, так как в нем меньше уравнений. Вывод основных расчетных уравнений проведем применительно к схеме рис. 1.14, содержащей два независимых контура. Положим, что в левом контуре по часовой стрелке течет контурный ток I 11, а в правой (также по часовой) - контурный ток I 22. Для каждого из контуров составим уравнения по второму закону Кирхгофа. При этом учтем, что в смежной ветви (с сопротивлением Rs) течет сверху вниз ток I 11 - I 22. Направления обхода контуров примем также по часовой стрелке. Для первого контура
или
Для второго контура
или
Рис. 1.14
В уравнении (1.24) множитель при токе I 11, являющийся суммой сопротивлений первого контура, обозначим через R 11, множитель при токе I 22 (сопротивление смежной ветви, взятое со знаком минус), – через R 12. В уравнении (1.25) множитель при токе I 22, являющийся суммой сопротивлений второго контура, обозначим через R 22, множитель при токе I11 (сопротивление смежной ветви, взятое со знаком минус), – через R 21.
Перепишем эти уравнения следующим образом:
Здесь
где R 11 и R 22 - полное или собственное сопротивление первого и второго контуров соответственно; E 11 и Е 22 - контурные ЭДС первого и второго контуров, равные алгебраической сумме ЭДС этих контуров; R 12 = R 21 -сопротивление смежной ветви между первым и вторым контуром, взятое со знаком минус, так как контурные токи по ветви протекают встречно. Если в схеме больше контуров, например три, то система уравнений в общем виде выглядит следующим образом:
В результате решения системы уравнений (1.26) какой-либо один или несколько контурных токов могут оказаться отрицательными. В ветвях, не являющихся смежными между соседними контурами, найденный контурный ток является истинным током ветви. В смежных ветвях через контурные токи определяются токи ветвей. Если в электрической цепи имеется n независимых контуров, то число уравнений тоже равно n. Общее решение системы n -уравнений относительно тока Ikk таково:
где D - определитель системы.
Алгебраическое дополнение ∆ km, получено из определителя ∆ путем вычеркивания k -го столбца и m -й строки и умножения полученного определителя на (-1) k + m. Составлению уравнений по методу контурных токов для схем с источниками тока присущи некоторые особенности. В этом случае полагаем, что каждая ветвь с источником тока входит в контур, замыкающийся через ветви с источниками ЭДС и сопротивлениями, и что токи в этих контурах известны и равны токам соответствующих источников тока. Если для схемы рис. 1.15 принять, что контурный ток I 11 = J течет согласно направлению часовой стрелки по первой и второй ветвям, а контурный ток I 22 = I 3 замыкается также по часовой стрелке по второй и третьей ветвям, то, согласно методу контурных токов, получим только одно уравнение с неизвестным током I 22:
Отсюда

Рис. 1.15
|
||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 918; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.181.112 (0.007 с.) |


 .
. .
. .
.
 . (1.24)
. (1.24)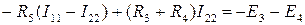
 . (1.25)
. (1.25)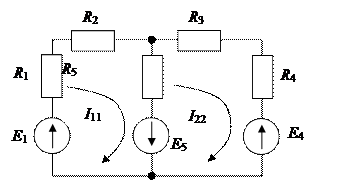
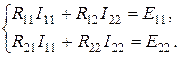

 (1.26)
(1.26) , (1.27)
, (1.27) .
. .
. и ток второй ветви I 2= I 11- I 22= J - I 22.
и ток второй ветви I 2= I 11- I 22= J - I 22.


