
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Активная, реактивная и полная мощности. Баланс мощностейСодержание книги
Поиск на нашем сайте
Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток.
Получим выражение для мгновенной мощности: Из (2.29) следует, мгновенная мощность изменяется с частотой Среднее значение мгновенной мощности за период T называют активной мощностью и обозначают буквой P:
При выводе (2.30) учтено равенство Учитывая из треугольника сопротивлений (рис.2.15) соотношение
Активная мощность измеряется в ваттах (Вт) и характеризует необратимое преобразование электрической энергии, которая выделяется в виде теплоты на участках цепи в активных сопротивлениях. В электрических двигателях потребляемая из сети активная мощность преобразуется в механическую мощность (за вычетом потерь в процессе преобразования) и является их основной характеристикой. Множитель Рассмотрим идеальные реактивные элементы (индуктивность и емкость). Активная мощность в этих элементах равна нулю, так как напряжение и ток в индуктивности или емкости различаются по фазе на 90o и В реактивных элементах отсутствуют необратимые потери электрической энергии, не происходит нагрева элементов. Происходит обратимый процесс в виде обмена электрической энергией между источником и приемником. Для качественной оценки интенсивности обмена энергией вводится понятие реактивной мощности Q. Преобразуем выражение (2.29) для мгновенной мощности:
где
Максимальное или амплитудное значение мощности p 2 называется реактивной мощностью: Q = где x, b – соответственно реактивные сопротивление и проводимость.
Амплитудное значение суммарной мощности p = p 1 + p 2 называется полной мощностью. Полная мощность, измеряемая в вольт-амперах (ВА), равна произведению действующих значений напряжения и тока:
Возьмем треугольник сопротивлений (рис.2.15) и умножим его стороны на квадрат тока в цепи. Получим подобный треугольник мощностей (рис. 2.17).
Рис. 2.17
Из треугольника мощностей получим соотношения между мощностями P, Q, S:
При расчете электрических цепей комплексным методом используют выражение комплексной мощности, равное произведению комплексного напряжения на сопряженный комплекс тока. Для цепи, имеющей активно-индуктивный характер, ток по фазе отстает от напряжения на угол
где
Для цепи, имеющей активно-емкостной характер, ток по фазе опережает напряжение
Активная мощность всегда положительна. Реактивная мощность в цепи, имеющей индуктивный характер, - положительна, а в цепи с емкостным характером - отрицательна. При выводе полученных соотношений предполагалось, что на зажимах цепи действует напряжение U. Если к зажимам цепи присоединен идеальный источник синусоидальной ЭДС с действующим значением E, то выражения (2.31)-(2.33), (2.35) для источника имеют следующий вид:
Из закона сохранения энергии следует, что для электрической цепи соблюдается закон баланса активных мощностей: активная мощность, генерируемая источниками, равна активной мощности, потребляемой всеми приемниками. Покажем, что соблюдается баланс и для комплексных, и, следовательно, для реактивных мощностей. Определим комплексные мощности для схемы (рис.2.7), содержащей идеальный источник синусоидальной ЭДС, последовательно соединенные активные и реактивные сопротивления приемника.
Запишем уравнение по второму закону Кирхгофа, умножим левую и правую части уравнения на сопряженный комплекс тока и учтем свойства произведения комплексно сопряженных чисел:
где
где
где Получим уравнение для комплексных мощностей источника и приемника:
Равенство (2.37) выражает баланс комплексных мощностей источника и приемника. При равенстве комплексных чисел равны по отдельности их вещественные и мнимые части, следовательно, уравнение (2.37) можно записать в следующей форме:
Из следует (2.38), что для электрической цепи соблюдается закон баланса реактивных мощностей: реактивная мощность, отдаваемая источниками, равна реактивной мощности, потребляемой всеми приемниками. Рассмотрим условие передачи источником максимальной мощности при заданном коэффициенте мощности приемника. В схеме на рис. 2.18 обозначены:
Рис. 2.18 Активная мощность может выделяться только в активных сопротивлениях цепи переменного тока. Активная мощность, выделяемая в нагрузке,
Активная мощность, развиваемая генератором
Из (2.39) видно, что выделяемая в нагрузке мощность будет максимальной, когда знаменатель минимален. Последнее имеет место при
Установим условие, при котором от источника к нагрузке будет передаваться наибольшая мощность:
отсюда От источника к нагрузке передается наибольшая мощность, когда
Величина наибольшей мощности
Режим передачи наибольшей мощности от источника к нагрузке называется согласованным режимом, а подбор сопротивлений согласно равенствам (2.41) - согласованием нагрузки с источником. В согласованном режиме величина КПД составляет:
Половина мощности теряется внутри источника. Поэтому согласованный режим не используется в силовых энергетических цепях. Этот режим используют в информационных цепях, где мощности могут быть малыми, и решающими являются не соображения экономичности передачи сигнала, а максимальная мощность сигнала в нагрузке.
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 872; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.113.171 (0.009 с.) |


 .
. (2.29)
(2.29) , в два раза превышающей частоту тока и напряжения.
, в два раза превышающей частоту тока и напряжения. (2.30)
(2.30)
 и из треугольника проводимостей (рис.2.16)
и из треугольника проводимостей (рис.2.16)  , получаем из (2.30) следующие выражения для активной мощности:
, получаем из (2.30) следующие выражения для активной мощности: (2.31)
(2.31) называется коэффициентом мощности. Коэффициент мощности является одной из важнейших характеристик электротехнических устройств, и повышение его до предельного значения
называется коэффициентом мощности. Коэффициент мощности является одной из важнейших характеристик электротехнических устройств, и повышение его до предельного значения 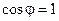 остается одной из основных задач энергосбережения.
остается одной из основных задач энергосбережения.

 - мгновенная мощность в активном сопротивлении;
- мгновенная мощность в активном сопротивлении; - мгновенная мощность в реактивном элементе (в индуктивности или в емкости).
- мгновенная мощность в реактивном элементе (в индуктивности или в емкости).
 (2.32)
(2.32) . (2.33)
. (2.33)
 Q =
Q =  ,
, 
 . (2.34)
. (2.34)

 ,
, - комплекс напряжения;
- комплекс напряжения;  - комплекс тока;
- комплекс тока;  - сопряженный комплекс тока;
- сопряженный комплекс тока;  - сдвиг по фазе между напряжением и током.
- сдвиг по фазе между напряжением и током. 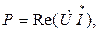 Q =
Q =  . (2.35)
. (2.35) .
.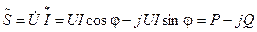
 Q =
Q = 
 ;
;  Q =
Q =  . (2.36)
. (2.36)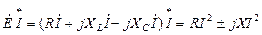 ,
,  ,
, - результирующее реактивное сопротивление.
- результирующее реактивное сопротивление. ,
,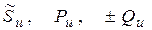 - полная комплексная, активная и реактивная мощности источника питания.
- полная комплексная, активная и реактивная мощности источника питания. ,
, активная и реактивная мощности, потребляемые элементами схемы.
активная и реактивная мощности, потребляемые элементами схемы. (2.37)
(2.37) . (2.38)
. (2.38) - полное, активное и реактивное сопротивления источника ЭДС,
- полное, активное и реактивное сопротивления источника ЭДС,  - полное, активное и реактивное сопротивления нагрузки.
- полное, активное и реактивное сопротивления нагрузки.
 . (2.39)
. (2.39) .
. .
. , т.е. при
, т.е. при  . Это означает, что реактивные сопротивления источника и нагрузки должны быть одинаковы по модулю и иметь разнородный характер. При индуктивном характере реактивного сопротивления источника реактивное сопротивление нагрузки должно быть емкостным, и наоборот:
. Это означает, что реактивные сопротивления источника и нагрузки должны быть одинаковы по модулю и иметь разнородный характер. При индуктивном характере реактивного сопротивления источника реактивное сопротивление нагрузки должно быть емкостным, и наоборот: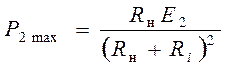 . (2.40)
. (2.40) .
. .
. ;
;  . (2.41)
. (2.41) . (2.42)
. (2.42) .
.


