
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрические цепи трехфазного токаСодержание книги
Поиск на нашем сайте 3.1.Основные определения.Трехфазная система ЭДС
Трехфазная цепь является совокупностью трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты и амплитуды, сдвинутые относительно друг друга по фазе на 120o. Участок трехфазной системы, по которому протекает одинаковый ток, называется фазой. Трехфазная цепь состоит из трехфазного генератора, соединительных проводов и приемников или нагрузки, которые могут быть однофазными или трехфазными. Трехфазный генератор представляет собой синхронную машину. На статоре генератора размещена трехфазная обмотка, состоящая из трех обмоток, оси которых пространственно смещены относительно друг друга на 120o. Магнитное поле в генераторе создается вращающимся ротором, на котором расположена обмотка возбуждения, питаемая постоянным током. По закону электромагнитной индукции в фазах генератора индуктируется симметричная трехфазная система ЭДС, в которой ЭДС одинаковы по величине и различаются по фазе на 120o. Трехфазные системы в настоящее время получили наибольшее распространение в энергетике. На трехфазном токе работают все крупные электростанции и потребители, что связано с рядом преимуществ трехфазных цепей перед однофазными, важнейшими из которых являются: - экономичность передачи электроэнергии на большие расстояния; - самым надежным и экономичным, удовлетворяющим требованиям промышленного электропривода является асинхронный двигатель с короткозамкнутым ротором; - возможность получения с помощью неподвижных трехфазных обмоток вращающегося магнитного поля, на чем основана работа синхронного и асинхронного двигателей, а также ряда других электротехнических устройств; - уравновешенность по мощности симметричных трехфазных систем, при которой суммарная мгновенная мощность всех фаз остается величиной постоянной и не зависящей от времени. Многофазная система ЭДС (напряжений, токов) называется симметричной, если она состоит из m одинаковых по модулю векторов ЭДС (напряжений, токов), сдвинутых по фазе друг относительно друга на одинаковый угол Графики мгновенных значений (рис.3.1, а) и соответствующие им изображения действующих значений трехфазной системы ЭДС на комплексной плоскости (рис.3.1, б), описываются следующими уравнениями:

Рис. 3.1
Комплексные значения фазных ЭДС симметричной трехфазной системы образуют симметричную звезду, и сумма их равна нулю:
Соответственно сумма мгновенных значений также в любой момент времени равна нулю
Схемы соединения трехфазных цепей На схемах трехфазных цепей начала фаз обозначают первыми буквами латинского алфавита (А, В, С), а концы - последними буквами (X, Y, Z). Направления ЭДС указывают от конца фазы обмотки генератора к ее началу. Каждая фаза нагрузки соединяется с фазой генератора двумя проводами: прямым и обратным. Получается несвязанная трехфазная система, в которой имеется шесть соединительных проводов. Чтобы уменьшить количество соединительных проводов, используют трехфазные цепи, соединенные звездой или треугольником. Если концы всех фаз генератора соединить в общий узел, а начала фаз соединить с нагрузкой, образующей трехлучевую звезду сопротивлений, получится трехфазная цепь, соединенная по схеме звезда-звезда. При этом три обратных провода заменяются одним, называемым нулевым или нейтральным ( Четырехпроводная трехфазная цепь, соединенная по схеме звезда-звезда с нулевым проводом, изображена на рис.3.2.
Рис. 3.2
Напряжения между началами фаз или между линейными проводами называют линейными напряжениями. Они обозначаются двумя индексами, например Напряжения между началом и концом фазы или между линейным и нейтральным проводами называются фазными напряжениями ( Токи в линейных проводах называют линейными токами ( При соединении звездой линейные провода соединены последовательно с фазами источника и приемника, поэтому линейные токи являются одновременно фазными токами I л = I ф. При наличии нейтрального провода ток в нейтральном проводе
В соответствии со вторым законом Кирхгофа запишем уравнения связи между линейными и фазными напряжениями:
Очевидно, что
Рис.3.3
На рис.3.3 представлена векторная диаграмма для симметричной системы напряжений. Как показывает ее анализ (лучи фазных напряжений образуют стороны равнобедренных треугольников с углами при основании, равными 300), в этом случае Обычно при расчетах принимается
Если конец каждой фазы обмотки генератора соединить с началом следующей фазы, образуется соединение в треугольник. К точкам соединений обмоток подключают три линейных провода, ведущие к нагрузке (рис.3.4).
Рис. 3.4
Как видно из рис. 3.4, в трехфазной цепи, соединенной треугольником, фазные и линейные напряжения одинаковы U л = U ф. Линейные (IA, IB, IC) и фазные (Iab, Ibc, Ica) токи нагрузки связаны между собой первым законом Кирхгофа:
На рис. 3.5 изображена векторная диаграмма трехфазной цепи, соединенной треугольником, при симметричной нагрузке состоящей из активных сопротивлений. В этом случае векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений.
Рис.3.5 Из векторной диаграммы следует, что при симметричной нагрузке лучи фазных токов образуют стороны равнобедренных треугольников с углами при основании равными 300. В этом случае соотношения между линейными и фазными токами Трехфазные цепи, соединенные звездой, получили большее распространение, чем трехфазные цепи, соединенные треугольником. Это объясняется тем, что, во-первых, в цепи, соединенной звездой, можно получить два напряжения: линейное и фазное. Во-вторых, при несимметричной нагрузке в фазах генератора или трансформатора, соединенных треугольником, в обмотке появляются дополнительные токи нулевой последовательности. Такие токи отсутствуют в фазах электрической машины, соединенных по схеме «звезд». В заключение отметим, что, помимо рассмотренных соединений трехфазных цепей звезда - звезда и треугольник – треугольник, на практике также применяются схемы звезда - треугольник и треугольник - звезда, схемы которых легко изображаются на примере рис.3.2, 3.3.
Расчет трехфазных цепей
Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно, все рассмотренные ранее методы расчета и анализа в символической форме в полной мере распространяются на них. Анализ трехфазных систем удобно осуществлять с использованием векторных диаграмм, позволяющих достаточно просто определять фазовые сдвиги между комплексными напряжениями и токами.
Схема звезда-звезда с нулевым проводом Трехфазная цепь по данной схеме (рис.3.2) имеет два узла и три независимых контура, поэтому ее удобнее всего рассчитать методом двух узлов. В общем случае при несимметричной нагрузке и учете сопротивления нулевого провода между нейтральными точками источника и нагрузки возникает узловое напряжение или напряжение смещения нейтрали. Это напряжение определяется по формуле
где Фазные напряжения нагрузки определяются по второму закону Кирхгофа с учетом (3.5):
Фазные токи определяются в соответствии с законом Ома:
Ток в нейтральном проводе определяется по формуле (3.2) или по закону Ома:
Трехфазные системы фазных При равномерной нагрузке фаз, когда комплексные проводимости фаз нагрузки одинаковы (
так как трехфазная система ЭДС симметрична и Трехфазная система фазных напряжений нагрузки также симметрична:
Фазные токи одинаковы по величине и также образуют симметричную трехфазную систему. В соответствии с (3.8) ток в нулевом проводе равен нулю и может быть исключен из схемы без изменения ее режима работы. Если в схеме звезда - звезда сопротивление нулевого провода мало Трехфазная система фазных токов определяется (3.7) и является несимметричной вследствие неравенства сопротивлений нагрузки
Рис. 3.6.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 3295; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.36.4 (0.006 с.) |

 . Трехфазную систему ЭДС обозначают следующим образом:
. Трехфазную систему ЭДС обозначают следующим образом:  -ЭДС с начальной фазой,
-ЭДС с начальной фазой,  - ЭДС, отстающую на 1200,
- ЭДС, отстающую на 1200,  - ЭДС, опережающую на 1200. Последовательность прохождения ЭДС через одинаковые значения (например, нулевые значения) называется последовательностью фаз.
- ЭДС, опережающую на 1200. Последовательность прохождения ЭДС через одинаковые значения (например, нулевые значения) называется последовательностью фаз. ,
,  ,
,  ;
; . (3.1)
. (3.1)

 .
. .Трехфазная система при соединении в звезду без нейтрального провода называется трехпроводной, с нейтральным проводом – четырехпроводной.
.Трехфазная система при соединении в звезду без нейтрального провода называется трехпроводной, с нейтральным проводом – четырехпроводной.
 (линейное напряжение между точками А и B). Модуль линейного напряжения обозначают U л.
(линейное напряжение между точками А и B). Модуль линейного напряжения обозначают U л. ,
,  ,
,  ).
). ,
,  ,
,  ). За положительное направление токов принимается направление от генератора к нагрузке. Модули линейных токов обозначают I л. Токи в фазах приемника или источника называют фазными токами I ф, а напряжения на них – фазными напряжениями U ф.
). За положительное направление токов принимается направление от генератора к нагрузке. Модули линейных токов обозначают I л. Токи в фазах приемника или источника называют фазными токами I ф, а напряжения на них – фазными напряжениями U ф. . (3.2)
. (3.2) ;
;  ;
;  . (3.3)
. (3.3) - как сумма напряжений по замкнутому контуру.
- как сумма напряжений по замкнутому контуру.
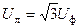 .
. . Тогда для случаяпрямого чередования фаз
. Тогда для случаяпрямого чередования фаз  ,
,  . С учетом этого на основании соотношений (3.3) могут быть определены комплексы линейных напряжений. Однако при симметрии напряжений эти величины легко определяются непосредственно из векторной диаграммы (рис.3.3). Направляя вещественную ось системы координат по вектору
. С учетом этого на основании соотношений (3.3) могут быть определены комплексы линейных напряжений. Однако при симметрии напряжений эти величины легко определяются непосредственно из векторной диаграммы (рис.3.3). Направляя вещественную ось системы координат по вектору  (его начальная фаза равна нулю), отсчитываем фазовые сдвиги линейных напряжений по отношению к этой оси, а их модули определяем в соответствии
(его начальная фаза равна нулю), отсчитываем фазовые сдвиги линейных напряжений по отношению к этой оси, а их модули определяем в соответствии  :
: ,
,  ,
,  .
.
 . (3.4)
. (3.4)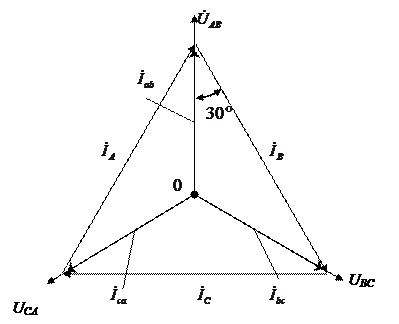

 .
. , (3.5)
, (3.5) - комплексные проводимости фаз нагрузки;
- комплексные проводимости фаз нагрузки;  - комплексная проводимость нулевого провода.
- комплексная проводимость нулевого провода. ,
,  ,
,  . (3.6)
. (3.6) . (3.7)
. (3.7) . (3.8)
. (3.8) напряжений (3.6) и токов (3.7) несимметричны, ток в нулевом проводе (3.8) не равен нулю.
напряжений (3.6) и токов (3.7) несимметричны, ток в нулевом проводе (3.8) не равен нулю. ), из (3.5) получаем
), из (3.5) получаем ,
, .
. .
. , то в схеме образуется три независимых контура и из (3.5) следует равенство нулю напряжения смещения нейтрали. Трехфазная система фазных напряжений нагрузки по (3.6) симметрична. Нулевой провод с нулевым сопротивлением в схеме звезда - звезда с несимметричной нагрузкой выравнивает несимметрию фазных напряжений нагрузки.
, то в схеме образуется три независимых контура и из (3.5) следует равенство нулю напряжения смещения нейтрали. Трехфазная система фазных напряжений нагрузки по (3.6) симметрична. Нулевой провод с нулевым сопротивлением в схеме звезда - звезда с несимметричной нагрузкой выравнивает несимметрию фазных напряжений нагрузки.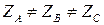 . По нулевому проводу протекает ток
. По нулевому проводу протекает ток 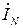 , определяемый по (3.2) как геометрическая сумма фазных токов. На рис. 3.6 в качестве примера приведена векторная диаграмма трехфазной цепи, соединенной по схеме звезда-звезда с нулевым проводом, имеющим нулевое сопротивление, нагрузкой которой являются неравные по величине активные сопротивления.
, определяемый по (3.2) как геометрическая сумма фазных токов. На рис. 3.6 в качестве примера приведена векторная диаграмма трехфазной цепи, соединенной по схеме звезда-звезда с нулевым проводом, имеющим нулевое сопротивление, нагрузкой которой являются неравные по величине активные сопротивления.



