
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные принципы и свойства линейных электрических цепейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основными свойствами линейных эл. цепей являются линейные соотношения м\д эл. величинами, а именно током и напряжением. В любой эл. цепи состоящей из линейных активных и пассивных элементов при изменении одной из величин (ЭДС, ток, напряжение, сопротивление) любая другая величина в разных ветвях будет зависеть от тока и напряжения других ветвей. Im = a + b * In Uk = c + d * Id; Uk = f + e * Ud; Для решения задач по расчету эл. цепей часто используют принцип суперпозиции (или взаимности). Принцип суперпозиции: В линейных цепях воздействие нескольких источников электрической энергии на данный элемент цепи можно рассматривать как результат воздействия на этот элемент каждого из источника в отдельности. Принцип суперпозиции целесообразно применять, когда эл. состояние цепи определенно для каких-либо источников ЭДС и токов и требуется проанализировать эл. состояние цепи при изменении ЭДС или тока одного из источника. В этом случаи нет необходимости вновь рассчитывать значении тока и напряжения от действия всех источников, а достаточно определить лишь частичные токи и напряжения от действия дополнительного ЭДС, которая будет определяться как разница между новым значением ЭДС и старым. При этом новое значение тока и напряжения на элементах будут определяться как алгебраическая сумма значений ранее действующей цепи и значений на дополнительной ЭДС. Следует отметить, метод суперпозиции не применим для расчета мощностей элементов электрической цепи, т.к. их значение пропорционально квадрату тока. Принцип взаимности применяется для электрических цепей с одним источником эл. энергии, и заключается в том что если ЭДС ветви m в цепи вызывает ток Ik к-ой ветви, то эта же ЭДС действуя в ветви к вызовет в ветви m такой же ток: Im = Ik
9. Эквивалентные преобразования пассивных участков электрических цепей Существует 4 основных вида соединения элементов: 1) последовательное; 2) параллельное; 3) соединение звездой; 4) соединение треугольником. 1. Iоб = I1 = I2 = In Uоб = U1 + U2 + Un Rоб = R1 + R2 + Rn 2. Iоб = I1 + I2 + In Uоб = U1 = U2 = Un 1/R = 1/R1 + 1/R2 + 1/Rn 3. В сложной ЭЦ встречаются соединения, которые нельзя отнести ни к последовательному, ни к параллельному. Рассмотрим мостовую цепь (используется в измерительных устройствах). В такой схеме часть цепи образует треугольник, вершинами которого являются 3 узла A, B, C, а сторонами являются сопротивления Rab, Rbc, Rca. Расчет такой цепи удобно производить, используя эквивалентную замену 3-х ветвей, соедин. треугольником, 3-мя ветвями, соедин. звездой. Определим соотношение эквивалентности между сопротивлениями обеих схем. Общее условие эквивалентности: напряжение и токи в ветвях не подвергнуты преобразованию, должны оставаться без изменения в любых режимах, в т.ч. при размыкании ветвей, присоединенных к узлам A, B, C. При отсоединении резисторов Rad от т. A в обеих схемах ток узла A и С, а также напряжение Ubc должны быть равны. А если это так, то и сопротивление Rbc на 1-й схеме должно быть равно сопротивлению между узлами В и С 2-й схемы. IC1 = IC2 IB1 = IB2 UBC1 = UBC2 RBC1 = RBC2
Аналогично, отсоединяя резистор RCD от т. C, получим след. выражение:
Решая систему полученных уравнений относительно RA+RB+RC, получим след. отношение:
Если резисторы различного сопротивления (для обратного перехода из звезды в треугольник):
Схема 1 (треугольник): Схема 2 (звезда):
B D B D
A E A
Метод контурных токов
Если цепь содержит много узлов и контуров, то расчет ЭЦ на основе применения з-в Кирхгофа связан с решением большого кол-ва уравнений. Число уравнений, составленных по методу контурных токов, равно количеству уравнений, составляемых по второму закону Кирхгофа. Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах. Введя понятие о контурных токах можно уменьшить кол-во уравнений на величину, равную составляемым по 1-му з-ну К-фа (у-1; где у – кол-во узлов). Порядок расчета: Выбираются независимые контуры, и задаются произвольные направления контурных токов. Контурные токи – условные (расчетные) токи, замыкающиеся в соответствующих контурах. Задача: найти все токи. После выбора положит. направления токов на схеме выбираются независим. контуры и положит. направления обхода каждого контура. Считается, что в каждом контуре циркулирует свой собственный контурный ток, направление которого совпадает с выбранным направлением в контуре. I1 = II; I2 = III - II; I3 = III; I4 = III –IIII; I5 = - IIII Для определения контурн. токов по 2-му закону К-фа составляются уравнения для выбранных контуров: 1) II (R1+R2) – III *R2 = E1 – E2 2) III (R2+R3 +R4) – II *R2 - IIII *R4 = E2 3) IIII (R4+R5) - III *R4 = - E3 Все резисторы, входящие в 1-й контур – R11, во 2-й - R22, в 3-й – R33.
R22 = R2 + R3 + R4 R33 = R4 + R5 Резисторы, общие с 1-м и 2-м контуром - R12 или R21, со 2-м и 3-м – R23 или R32, 1-м и 3-м - R13 или R31.
R13 = R31 = 0 R23 = R32 = R4 Источники тока или напряжения, входящие в 1-й контур – Е11 = Е1 - Е2; 2-й: Е22 = Е2; 3-й: Е33 = - Е3 Система уравнений будет представлена в след. виде:
- R21 * II + R22 * III – R23 * IIII = E22 - R31 * II – R32 * III + R33 * IIII = E33 На главной диагонали все положительные, остальные – отрицательные. Матричная форма записи системы удобна для решения системы при помощи ЭВМ. При расчете электрических цепей изложенным методом всегда стремятся к тому, чтобы число контурных токов, замыкающихся через каждую из ветвей, было по возможности минимальным. С этой целью обычно выбирают каждый контур в виде ячейки руководствуясь указанным выше правилом выбора независимых контуров при составлении уравнений на основании второго закона Кирхгофа, что возможно для любой планарной схемы. Положительные направления контурных токов можно выбирать и произвольно, т. е. независимо от положительных направлений токов в ветвях.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 893; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |


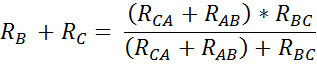

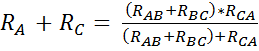





 C С
C С R11 = R1 + R2
R11 = R1 + R2 R12 = R21 = R2
R12 = R21 = R2 R11 * II - R12 * III - R13 * IIII = E11
R11 * II - R12 * III - R13 * IIII = E11


