Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. 1. Основные элементы электрических цепей. Эквивалентные схемы источников энергии.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
I. 1. Основные элементы электрических цепей. Эквивалентные схемы источников энергии. Основные элементы электрических цепей. Электрическая цепь – это совокупность устройств, предназначенных для передачи, распределения и взаимного преобразования энергии. Основнымиэлементами являются источники и приемники электрической энергии, которые соединяются между собой проводами, а также измерительные приборы(амперметр, вольтметр….). ЭДС можно определить как работу сторонних (не электрических) сил присущих данному источнику затрачиваемую на перемещение единичного положительного заряда внутри источника от вывода с меньшим потенциалом к выводу с большим. Источник тока – это идеализированный источник питания, который создает ток I не зависящий от сопротивления нагрузки, к которой он присоединен, а его ЭДС и внутреннее сопротивление равны бесконечности. Отношение (E к Rвн) бесконечно больших величин равно конечной величине – току Iк источника тока.
Эквивалентные схемы источников энергии. При расчете и анализе электрических цепей реальный источник электрической энергии с конечным значением Rвн заменяют расчетным эквивалентом. В качестве эквивалента может быть взят: А) Источник ЭДС E с последовательно включенным сопротивлением Rн, равным внутреннему сопротивлению реального источника. Б) Источник тока с током Iк=E/Rвн и параллельно с ним включенным сопротивление Rвн.
Идеальный источник ЭДС нельзя заменить идеальным источником тока. I. 2. Основные понятия и законы электрических цепей.
Закон Ома для активного участка цепи.
Для Рис. 1:
Для Рис. 2 Эти уравнения математически выражают закон Ома для участка цепи содержащего источник ЭДС.
Первый закон Кирхгофа. Алгебраическая сумма токов в узле равна нулю. (Токи, входящие в узел, берутся с одним знаком, а токи выходящие с противоположным) Число уравнений по 1-му закону Кирхгофа можно составить n-1, где n-число узлов.
Второй закон Кирхгофа. В любом замкнутом контуре алгебраическая сумма падений напряжений равняется алгебраической сумме ЭДС. Произвольно выбираем направление обхода контура и те напряжения и ЭДС, которые совпадают с выбранным направлением берутся с «+», а не совпадающие с «-». Делая обход по соединенным узлам можно получить замкнутый контур. Число уравнений по 2-му закону Кирхгофа можно составить Nв-n+1, где n-число узлов, Nв - число веток. Число уравнений по 2-му закону Кирхгофа равняется числу независимых контуров. Контур – это путь проходящий по замкнутым узлам, при этом каждый узел должен встречаться один раз. Независимый контур – чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по 2-му закону Кирхгофа. I. 3. Баланс мощности 1. Pист=Pпотр (потребляемая мощность должна равняться мощности вырабатываемой) Pпотр =
А) B)
P=EkIk P= - EkIk
С) D)
P=JkUAB P= - JkUAB
UAB ищется пр 2-му з-ну Кирхгофа
I. 4. Метод контурных токов
I. 6. Метод Наложения Если есть несколько источников питания, то можно рассчитывать цепь под действием каждого источника отдельно и найти частичные токи.
Найти реальные токи как сумму частичных токов. При этом знаки в этой сумме зависят от направления частичных токов. Если оно совпадает и реальным током, то «+», иначе «-».
По МН нельзя искать мощность. Когда мы определяем составляющую тока от одного источника, то другие источники – аннулируются, но остается их сопротивление. Если это идеальный источник ЭДС – его надо закоротить. Если это идеальный источник тока – его надо разорвать. Начальные условия В простейшем случае переходному процессу предшествует установившийся режим и заканчивается он также установившимся режимом. Значения токов и напряжений в электрической цепи в момент времени t = 0 называются начальными значениями или начальными условиями. Причем эти значения при коммутации могут изменяться или оставаться постоянными в первый момент времени. Начальные значения, не изменяющиеся при коммутации и определяемые по состоянию цепи до нее, называются независимыми начальными значениями. Очевидно, к ним относятся токи в индуктивностях и напряжения на емкостях. Остальные начальные значения величин называются зависимыми и определяются по состоянию цепи после коммутации с учетом независимых начальных значений. Значения токов и напряжений в цепи после переходного процесса, т.е. при t = µ, называются установившимися значениями. Начальные и установившиеся значения величин можно определить с помощью любых методов расчета электрических цепей в установившемся режиме, например, с помощью уравнений Кирхгофа.
Для t=0 можно емкость заменить на источник ЭДС, величина которого равна Uc(0) и направить его против Uc(0). Индуктивность можно заменить на источник тока величиной IL(0) и направить по IL.
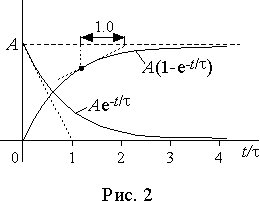
Эту схему нужно составлять для после коммутационного режима! Постоянная времени. Коэффициент t, имеющий размерность времени, определяет скорость изменения величины a (t) и называется постоянной времени экспоненты. Чем меньше постоянная времени, тем быстрее протекает переходный процесс. Выберем произвольно два момента времени, отстоящие друг от друга на время t. Значения a (t) для этих моментов - a 1(t) = A e- t /t и a 2(t) = A e-(t+ t )/t , а их отношение a 1(t)/ a 2(t) = e-(t - t-t )/t = e, следовательно, в течение постоянной времени величина a (t) изменяется в е- раз. Графически это свойство экспоненты проявляется в том, что касательная к ней в любой точке пересекает установившееся значение в точке, отстоящей по времени от точки каcания на величину t (рис. 2). Теоретически экспонента в течение конечного интервала времени не достигает установившегося значения, т.е. любой переходный процесс должен продолжаться бесконечно. Однако при t = 3t значение экспоненты отличается от установившегося на 5%. Поэтому интервал времени равный 3t считают длительностью переходного процесса.
I. 1. Основные элементы электрических цепей. Эквивалентные схемы источников энергии.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.91.116 (0.011 с.) |







 1. Закон Ома для участка цепи, не содержащего источник ЭДС: устанавливает связь между током и напряжением на участке ab(см.рис):
1. Закон Ома для участка цепи, не содержащего источник ЭДС: устанавливает связь между током и напряжением на участке ab(см.рис):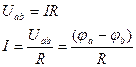

 Закон позволяет найти ток этого участка по известной разности потенциалов (Ua-Uc) на концах участка цепи и имеющейся на этом участке ЭДС Е.
Закон позволяет найти ток этого участка по известной разности потенциалов (Ua-Uc) на концах участка цепи и имеющейся на этом участке ЭДС Е.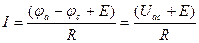

 -потребляемая мощность
-потребляемая мощность Pист –мощности источников ЭДС
Pист –мощности источников ЭДС