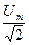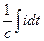Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. 8. Метод эквивалентного генератораСодержание книги
Поиск на нашем сайте
По отношению к выделенной ветви двухполюсник можно заменить эквивалентным генератором, эдс которого равно напряжению холостого хода на зажимах выделенной ветви, а внутреннее сопротивление равно входящему сопротивлению двухполюсника. Для расчета тока методом эквивалентного генератора нужно соблюсти последовательность: 1) найти напряжение на зажимах разомкнутой ветви (считать оставшуюся ветвь активным двухполюсником) 2) определить ε генератора=Uхх (напряжение между точками обрыва) 3) определить входное сопротивление всей схемы относительно точек отрыва при закороченных источниках эдс и разомкнутых ветвях с источниками тока 4) подсчитать ток в искомой ветке по формуле: Для того, чтобы в сопротивлении нагрузки выделилась максимальная мощность нужно выяснить соотношения между сопротивлением R и входным сопротивлением двухполюсника
Так как Теперь можно найти максимальную мощность, которая может быть выделена в нагрузке R P= P= Рполн=
Если Выбор сопротивления нагрузки R, равного входному сопротивлению Rвх активного двухполюсника называется согласованием нагрузки. Если мощность Р значительнее, то работа с таким низким КПД как 0,5 недопустима, но если Р мало и составляет всего несколько милливатт, то низким КПД можно пренебречь, так как будет достигнута главная цель-датчик отдает нагрузке мах возможную мощность. I. 9. Преобразование цепей
(

2. Преобразование параллельно соединённых ветвей, содержащие источник ЭДС и источники тока
R1 R3 R4 U
E1
Из выражения для Eэ и gэ видно, что E эквивалентно зависит от E и от g (проводимость), а gэ зависит от проводимостей. При определении Eэ в числителе те ЭДС, которые совпадают с направлением выбора Eэ, берутся со знаком «+», и наоборот.
Если в схеме к узлам 1 и 2 подключены ветви с источниками тока, то при вычислении Eэ нужно учесть токи источников:
У источников тока знаки берутся также. 3. Преобразование звезды в треугольнике.
RII
c b I1=Iab – Ica (1)
II. 1. Основные определения, элементы электрической цепи. Максимальные, средние и действующие значения синусоидальных токов, напряжений и Э.Д.С. Переменный ток – ток, изменяющийся во времени. Значение тока в любой данный момент времени, называется мгновенным значением (i) Периодические токи – переменные токи, значения которых повторяются через равные промежутки времени(периоды). f(t)=f(t+T)
Мгновенное значение синусоидального тока:
Среднее значение: Действующее(среднее квадратичное): I численно равно такому значению переменного тока, при котором за T выделяется такое же количество теплоты что и при постоянном токе.
r- сопротивление, T –период
Действующее значение ЭДС:
Действующее значение напряжения: Элементы:
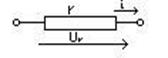
Резистивный элемент:
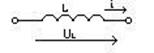
Индуктивный элемент:
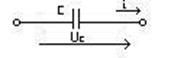
Емкостный элемент:
II. 2. Законы Кирхгоффа в синусоидальном токе Алгебраическая сумма мгновенных значений токов в узле равна 0. Причем, входящие берутся с одним знаком, а выходящие – с другим. Можно написать n-1 уравнение, где n – число узлов. В любом замкнутом контуре алгебраическая сумма мгновенных значений падений напряжений равна алгебраической сумме мгновенных значений ЭДС. Причем, если встречается индуктивность, то тогда записываем след слагаемое: L*di/dt ---------------------- емкость -------------------------------------------------------: ---------------------------------резистор-------------------------------------------------------: i*r Произвольно определяем направление обхода контура, если ЭДС совпадает с направлением обхода контура, то берем «+Е» Кол-во уравнений: N-n+1, N-число контуров.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 247; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.151.11 (0.02 с.) |

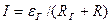 здесь к активному двухполюснику подключена нагрузка R, через которую потечет ток I и выделится мощность.
здесь к активному двухполюснику подключена нагрузка R, через которую потечет ток I и выделится мощность. 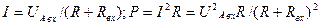
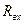 , для этого определим первую производную Р по
, для этого определим первую производную Р по 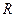 и приравнять к 0.
и приравнять к 0.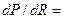 (
(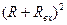 -
- 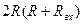 )/(
)/(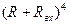 )=0→
)=0→ 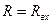 ( * ).
( * ).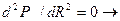 (*)соответствует максимум функции
(*)соответствует максимум функции  P=f(R)
P=f(R)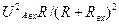 &R=
&R= 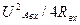
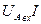 =
= 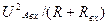 - полная мощность
- полная мощность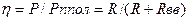
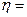 0,5
0,5








 R R U
R R U

 E
E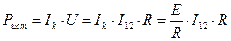
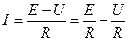
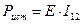
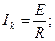
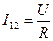 )
)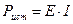 , Pист – мощность источника ЭДС.
, Pист – мощность источника ЭДС. Обратное преобразование:
Обратное преобразование:




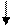


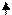


 Ik
Ik 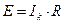











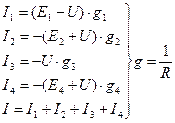
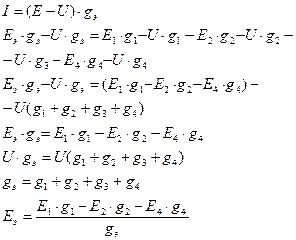
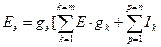 ]
] а
а
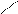




 I1 I1
I1 I1
 a
a
 Ica Iab
Ica Iab


 R1 RIII RI
R1 RIII RI


 I3 0 I2 c b
I3 0 I2 c b

 R3 R2 I3 Ibc I2
R3 R2 I3 Ibc I2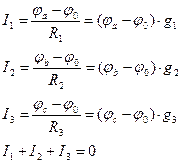
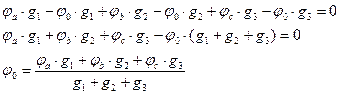
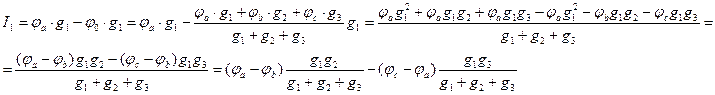 (
(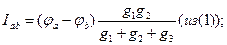
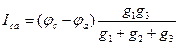 )
)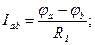
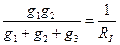
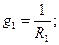
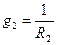
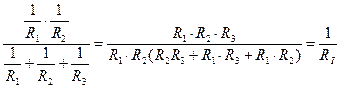
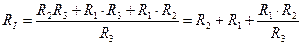
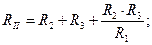
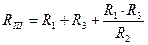
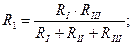
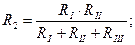
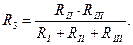
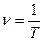
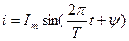
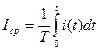
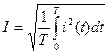
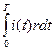 =
= 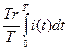 =
= 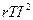
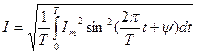 =
= 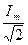
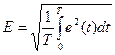 E=
E= 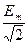
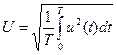 U=
U=